1. Понятие дискретной динамической системы
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
32. Помеченные сети Петри. Пример.
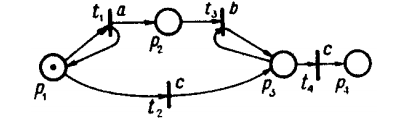
В зависимости от вида получают различные классы языков СП. Если Σ – частичная функция, т.е. некоторым переходам не сопоставляется никакой символ из А, то эти непомеченные переходы называются λ-переходами и помечаются одним и тем же «пустым» символом λ. Частичные функции удобны в тех случаях, когда при моделировании системы нужно ввести вспомогательные переходы, не связанные непосредственно с событиями системы, а используемые для некоторых специальных целей моделирования. С помощью λ-переходов также можно «маскировать» события, которые не должны рассматриваться в данной задаче моделирования. 33.Префиксный язык сети Петри. Свободный терминальный язык сети Петри. Терминальный язык сети Петри. Пример.Пусть τ  T* - допустимая последовательность запусков переходов СП C, (C, Σ) – помеченная сеть, Σ (τ) T* - допустимая последовательность запусков переходов СП C, (C, Σ) – помеченная сеть, Σ (τ) A* - помечающая последовательность, соответствующая τ. A* - помечающая последовательность, соответствующая τ.Если L(C) – свободный язык СП C, то множество {Σ (τ)| τ  L(C)} называется префиксным языком помеченной сети (C, Σ); если A=T, то свободный язык СП совпадает с ее префиксным языком. L(C)} называется префиксным языком помеченной сети (C, Σ); если A=T, то свободный язык СП совпадает с ее префиксным языком.Пусть μ0 – начальная маркировка СП, а μt – некоторая фиксированная терминальная маркировка. Множество L(C,μ0,μt)={τ  T*|δ(μ0,τ)=μt} называется свободным терминальным языком СП C, т.е. свободный терминальный язык состоит из всех последовательностей переходов, ведущих от начальной маркировки μ0к некоторой фиксированной терминальной маркировке μt. Такие последовательности образуют подмножество терминальных последовательностей СП. T*|δ(μ0,τ)=μt} называется свободным терминальным языком СП C, т.е. свободный терминальный язык состоит из всех последовательностей переходов, ведущих от начальной маркировки μ0к некоторой фиксированной терминальной маркировке μt. Такие последовательности образуют подмножество терминальных последовательностей СП.Соответственно множество {Σ(τ)|τ  L(C,μ0,μt)} образует терминальный язык помеченной сети (C,Σ). L(C,μ0,μt)} образует терминальный язык помеченной сети (C,Σ).Пример: пусть τ1, τ2 - допустимые последовательности запусков переходов некоторой СП, ведущие из начальной маркировки в: τ1=t1t1; τ2=t2t4t3t3t3. Тогда префиксный язык: {t1, t1t1, t2t4t3t3t3, t2t4t3t3, t2t4t3, t2t4, t2}; терминальный язык: {t1t1, t2t4t3t3t3}. 34.Три вида помечающих функций для сетей Петри.Вид 1. Σ(tj)=tj для 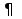 tj tj T – свободная помечающая функция (ПФ). T – свободная помечающая функция (ПФ).Вид 2. Σ(tj) определена для 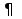 tj tj T пометки – символы из А. Это всюду определенная помечающая функция. Сеть без λ-переходов. T пометки – символы из А. Это всюду определенная помечающая функция. Сеть без λ-переходов.Вид 3. Σ(tj) не определена для некоторых переходов, т.е. tj  T– такой переход, tjпомечается пустым символом λ и объявляется λ-переходом. Тогда это частично определенная помечающая функция. T– такой переход, tjпомечается пустым символом λ и объявляется λ-переходом. Тогда это частично определенная помечающая функция. |