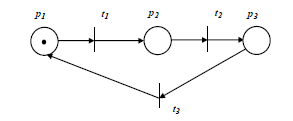
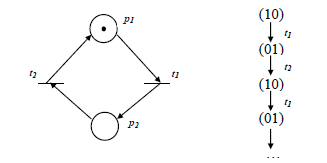
1. Понятие дискретной динамической системы

• Название: 1. Понятие дискретной динамической системы
• Дата: 23.11.2018
• Размер: 0.51 Mb.
• Имя файла: tmp_4118-Otvety_k_ekzamenu_po_predmetu_Teoria_vychislitelnykh_pr.docx
• Тип: Документы; #57412
• страница: 13 из 15

38. Основные задачи анализа сетей Петри: задачи достижимости и покрываемости. Пример.

Задача достижимости: для СП (С,μ₀) и некоторой маркировки μ' проверить включение μ'R(C,μ₀).

• 
  Проблема тупиков: принадлежит ли данная тупиковая маркировка множеству достижимости маркированной СП.
  
• 
  Проблема взаимного исключения: могут ли в процессе функционирования СП быть маркировки, в которых в обеих позициях есть фишки.
  

Задачу покрываемости можно сформулировать следующим образом.

Для данной СП С с μ и некоторой маркировки μ'R(C,μ) определить, существует ли достижимая изμ' маркировка μ'' такая, что μ''μ' (μ'' покрывает μ', а μ' - покрывается μ'')?

μ0=(100) покрывается маркировкой μ'=(100), которая получена в результате запуска последовательности переходов σ=(t1t2t3).

39.Основные задачи анализа сетей Петри: задачи эквивалентности.

Функционирование СП описывается множеством достижимости или множеством последовательностей запусков. Тогда:

1) выяснить, имеются ли в маркированной СП пассивные переходы и позиции (которые никогда не будут иметь фишек), и удалить их вместе с входными и выходными дугами.

2) Пусть две маркированные СП имеют одинаковое число переходов, причем между переходами первой и второй сети установлено взаимно-однозначное соответствие (количество позиций может совпадать, а может не совпадать). Требуется показать, что между множествами последовательностей запусков переходов сетей имеется взаимно-однозначное соответствие.

3) Пусть две маркированные сети Петри имеют одинаковое число позиций, причем между позициями первой и второй сети установлено взаимно-однозначное соответствие (количество переходов может совпадать, а может не совпадать). Требуется показать, что между множествами достижимости сетей имеется взаимно-однозначное соответствие.

По сути, все эти задачи связаны с преобразованием исходной сети в новую сеть, которая в определенном смысле эквивалентна исходной, но возможно, имеет другую структуру.

Редукцией относительно некоторого набора свойств {z₁, z₂, …, z_k} называется преобразование сети Петри (C,μ₀) в сеть (C', μ₀'), таким образом, что 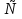|PT|>|P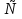'T'|, и все свойства из данного набора сохраняются (сеть Петри сокращается, что упрощает ее последующий анализ).

40. Методы анализа сетей Петри: дерево достижимости. Пример. Граничная, терминальная, дублирующая, внутренняя вершины (маркировки).

Дерево достижимости – ориентированное корневое дерево, вершинам которого соответствуют возможные маркировки, а дугам – разрешенные переходы. Корневой вершине соответствует μ0. Из вершины исходят дуги, соответствующие разрешенным в этой маркировке переходам.

Граничная вершина – вершина, полученная на очередном шаге построения ДД, которая в настоящий момент обрабатывается.

Терминальная вершина соответствует маркировке, в которой не разрешен ни один переход (тупиковой маркировке).

Дублирующая вершина соответствует маркировке, уже полученной в ДД.

Внутренняя вершина – вершина ДД, ни одной их перечисленных.