1. Понятие дискретной динамической системы
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
4.Отношение F. Отношение М.Ситуации siи sj находятся в отношении M, если существует траектория, в которую входят si и sj, причем siпредшествует sj(длина траектории - любая); отношение sjMsk означает возможность перехода из sj в sk. Это отношение транзитивное, поскольку если siMsj и sjMsk, то siMsk. В АП возможны случаи sjMsk и sjMsl, k не равно l. Заметим, что если для некоторого sjсуществует единственная ситуация, для которой sjMsk, то обязательно sjFsk. Отношение непосредственного следования F не восстанавливается однозначно по отношению M. Отношение М можно выразить через степени отношения F: Запись sjFnsk означает наличие (n-1) промежуточных ситуаций si1, si2,..., sin таких, что sjFsi1, si1Fsi2,…,sin-1Fsk. В этом случае в графе существует траектория, содержащая n+1 вершину и n дуг и ведущая из sj в sk. Если ситуации si и sk некоторого АП связаны отношением siMsk (siFnsk при некотором n), то фрагмент процесса, содержащий все траектории, ведущие из si в sk, назовем переходом si – sk 5.Отношение эквивалентности. Классы эквивалентности. Свойства классов эквивалентности.На множестве S введем бинарное отношение Е следующим образом: а) если sjMsk и skMsj, тоsjEsk; б) 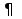 sjS sjEsj. sjS sjEsj.Как легко проверить, это отношение является рефлексивным, симметричным и транзитивным, т.е. является отношением эквивалентности на множестве ситуаций. Известно, что отношение эквивалентности разбивает множество на классы эквивалентности: подмножества, что любые состояния из одного класса эквивалентны, а из разных классов не эквивалентны. Из определения следует, что любой класс эквивалентности является подмножеством одного из множеств: I, R, S\(I R), поскольку отношение эквивалентности означает наличие цикла, содержащего соответствующие ситуации. Если множество ситуаций АП разбить на классы эквивалентности e(1), e(2),..., e(р), то между ними естественным образом возникает отношение непосредственного следования 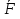 . Запись e(i) . Запись e(i) 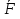 e(j) означает, что из некоторой ситуации класса e(i) можно попасть непосредственно (т.е. применением отношения F) в какую-либо ситуацию класса e(j). e(j) означает, что из некоторой ситуации класса e(i) можно попасть непосредственно (т.е. применением отношения F) в какую-либо ситуацию класса e(j).Рассмотрим последовательности классов эквивалентности вида: П=(e(1), e(2),..., e(р)). Последовательность называется допустимой, если e(i) 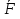 e(i+1) при i= e(i+1) при i=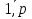 . Допустимая последовательность называется максимальной, если она не является отрезком никакой допустимой последовательности. . Допустимая последовательность называется максимальной, если она не является отрезком никакой допустимой последовательности. |
