1. Понятие дискретной динамической системы
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
14.Редукция диаграммы переходов.Редукцию ДП можно осуществить по множеству ситуаций, порожденному теми или иными компонентами ситуаций. В этом случае сначала из всего множества ситуаций S оставляют те, входные компоненты которых попали в выделенное множество значений входной компоненты X*. Таким образом, получаем множество ситуаций S*. Далее редукция строится по полученному множеству ситуаций S*. Первые два элемента вектора полного состояния выберем в качестве входных компонент, последние два – в качестве выходных компонент. 15. Основная идея теории комплектов, сравнение с теорией множеств. Свойства комплектов.В теории СП комплект - набор элементов из некоторой конечной области D (аналогично множеству).
Свойства комплектов Пусть х и B: #(х,В)  0. 0.Если #(х,В)>0, то обозначается: х  B. Если #(х,В)=0, то обозначается: х B. Если #(х,В)=0, то обозначается: х В. Пустой комплект: В. Пустой комплект: . .
16. Операции над комплектами. Пространство комплектов.Пусть А и В – комплекты. Определим для них операции:
Нетрудно видеть, что:
Пространство комплектов Dn – множество всех таких комплектов, что элементы их принадлежат D, и ни один элемент не входит в комплект более n раз. Таким образом, для любого комплекта В  Dn имеем: Dn имеем:1) если х  В, то х В, то х D, D,2) для 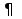 х х В: #(х, В) В: #(х, В) n. n.Множество D∞ - множество всех комплектов над областью D без каких-либо ограничений на число экземпляров элемента в комплекте. Если D={d1, d2, ..., dm}, то существует естественное соответствие между каждым комплектом B над D и m-мерным вектором f=(f1, f2, ..., fm) по правилу fi=#(di,B). Это соответствие называется отображением Париха. | ||||||||

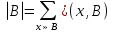
 В.
В.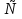 В: #(х, А
В: #(х, А В: #(х, А
В: #(х, А