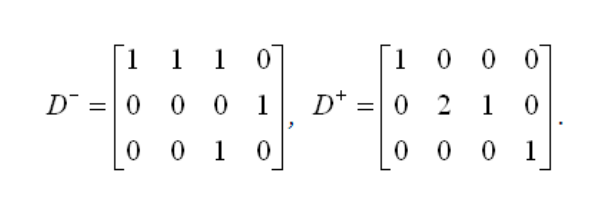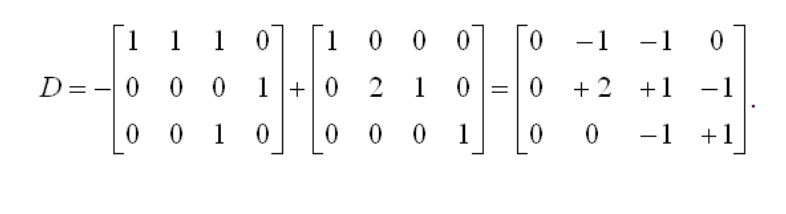1. Понятие дискретной динамической системы
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
44.Лемма 2 для доказательства теоремы о конечности дерева достижимости сети Петри.Расширенным множеством натуральных чисел будем называть множество натуральных чисел, дополненное символом ω. Лемма 2. Всякая бесконечная последовательность из расширенного множества натуральных чисел содержит бесконечную неубывающую подпоследовательность. Доказательство. Возможны два случая:
Получаем бесконечную неубывающую последовательность x0≤х1≤x2≤x3≤.... (чтд) 45. Лемма 3 для доказательства теоремы о конечности дерева достижимости сети Петри.Лемма 3. Всякая бесконечная последовательность n-мерных векторов над расширенным множеством натуральных чисел содержит бесконечную неубывающую подпоследовательность. Доказательство. Доказываем индукцией по n, где n – размерность векторного пространства. 1. Случай n =1 это лемма 2. 2. Допустим: лемма верна для размерности n, докажем ее справедливость для (n+1). Сопоставим каждому (n+1)-мерному вектору из последовательности n-мерный вектор, полученный удалением последней координаты. По предположению индукции, из полученной последовательности n-мерных векторов можно извлечь неубывающую подпоследовательность. Добавим к элементам этой подпоследовательности (n+1)-ю координату из исходной последовательности. Выбрав из полученной последовательности [(n+1)–х] координат неубывающую последовательность получим «подподпоследовательность» исходной последовательности с нужными свойствами. 46. Терема о конечности дерева достижимости сети Петри.Теорема: Усеченное дерево достижимости СП конечно. Доказательство (от противного). Допустим, что существует бесконечное усеченное ДД. Число дуг, исходящих из каждой вершины дерева конечно. Все условия леммы 1 выполняются и в дереве существует бесконечный путь, исходящий из корня: х0, x1, x2, .... Каждой вершине соответствует маркировка, являющаяся n-мерным вектором над расширенным множеством натуральных чисел. По лемме 3 бесконечная последовательность µ[x0],µ[x1],µ[x2],… имеет бесконечную неубывающую последовательность: µ[xi0]  µ[xi1]≤µ[xi2]≤… µ[xi1]≤µ[xi2]≤… Обратимся к алгоритму построения усеченного ДД. В соответствии с пунктом 2: если µ[xij]= µ[xij+1], то µ[xij+1], – дублирующая и из соответствующей вершины дуги не строятся. Это позволяет исключить знак равенства. Тогда µ[xi0]  µ[xi1] µ[xi1]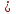 µ[xi2] µ[xi2]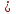 … …В соответствии с алгоритмом построения УДД, если µ[x] < µ[y] и x и y находятся на одном пути от корня, то в маркировке µ[y] по меньшей мере одна компонента равна ω. Тогда µ[xi1] содержит по меньшей мере 1 символ ω; …; µ[xin] - n символов ω. Но тогда, так как векторы n-мерные, µ[xin+1] также содержит n символов ω и является дублирующей к маркировке µ[xin] и это противоречит тому, что последовательность является бесконечной. Противоречие доказывает справедливость теоремы. 47. Решение задачи безопасности и ограниченности сетей Петри на основе дерева достижимости.СП ограничена тогда и только тогда, когда символ 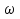 отсутствует в ее дереве достижимости. отсутствует в ее дереве достижимости.В этом случае покомпонентное исследование вершин усеченного ДД позволяет установить безопасность или ограниченность для каждой отдельной позиции, после чего сделать вывод о сети в целом. Наибольшее значение компоненты маркировки, соответствующей некоторой позиции есть граница числа фишек этой позиции. Если граница для всех позиций не превышает 1, сеть безопасна. 48. Решение задачи сохранения сетей Петри на основе дерева достижимости.Напомним, что маркированная СП С=(P,T,I,O,μ0) называется сохраняющей по отношению к вектору взвешивания w=(w1, w2,..., wn), n=|Р|, wi>0 для  i, если для всех μ' i, если для всех μ' R(C, 0) R(C, 0) 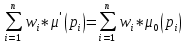 Строго сохраняющая СП является сохраняющей по отношению к вектору взвешивания w=(1, 1, ..., 1). Рассмотрим задачу нахождения вектора взвешивания, по отношению к которому сеть будет сохраняющей, используя усеченное ДД. Естественно, что данная задача решается только для деревьев, в которых отсутствует символ 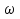 . .Пусть усеченное ДД имеет k вершин: x1, x2, …, xk. Для набора вершин составляется система, имеющая k равенств, n неравенств и (n+1) неизвестных (w1, w2, …, wn, С). 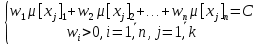 49.Решение задачи покрываемости и достижимости сетей Петри на основе дерева достижимости. Проблемы, возникающие в случае наличия неограниченной позиции. Пример.В задаче покрываемости мы хотим для данной маркировки μ' определить, достижима ли маркировка μ''  μ'. Строим для начальной маркировки усеченное ДД. Затем ищем любую вершину х с μ[x μ'. Строим для начальной маркировки усеченное ДД. Затем ищем любую вершину х с μ[x μ'. Если такой вершины не существует, маркировка μ' не покрывается никакой достижимой маркировкой; если она найдена, μ[х] дает достижимую маркировку, покрывающую μ'. μ'. Если такой вершины не существует, маркировка μ' не покрывается никакой достижимой маркировкой; если она найдена, μ[х] дает достижимую маркировку, покрывающую μ'.Задача достижимости маркировки μ'' из начальной маркировки μ' решается поиском вершины усеченного ДД с маркировкой μ'' Усеченное ДД не всегда можно использовать для решения задач покрываемости и достижимости. Ранее уже обсуждалось, что решение указанных задач затруднено в случае, когда ДД содержит символ 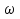 . Если дерево не содержит символ . Если дерево не содержит символ 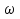 , то эти за , то эти задачи успешно решаются. Пример: рисунок
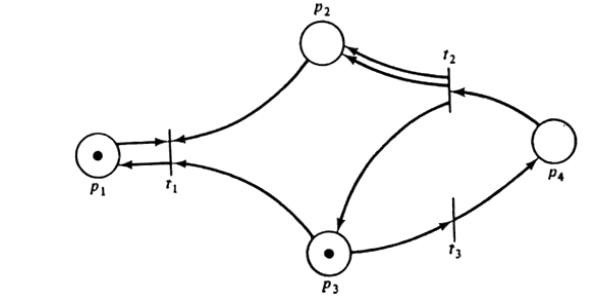
50. Анализ свойств сетей на основе использования матричного подхода: матрицы D-, D+, пример построения матриц для сети Петри.
D–: Первая строка отвечает за переход t1. Первые три элемента в строке равны 1, так как из позиций p1, p2, p3 идут дуги к переходу t1. 51.Составная матрица изменений (матрица инцидентности). Пример. Замечания по применению матричного подхода.
52.Решение задачи достижимости с помощью матричного подхода. Замечание. Пример.Для данной СП С=(P, T, D-, D+) требуется определить, достижима ли маркировка μ' из маркировки μ. Если маркировка μ' достижима из μ, то существует последовательность (возможно пустая) запусков переходов σ, которая приводит из μ к μ'. Следовательно, f(σ) является целым неотрицательным решением следующего матричного уравнения относительно х: μ'=μ+xD,где x=f(σ)=(x1, x2, …, xm), m=|T|. Пример. Для D=  ребуется определить, достижима ли маркировка μ'=(0, 1, 0) из μ=(0, 0, 2). ребуется определить, достижима ли маркировка μ'=(0, 1, 0) из μ=(0, 0, 2).Для решения данной задачи воспользуемся уравнением μ'=μ+xD: (0, 1, 0)=(0, 0, 2)+(x1, x2, x3) 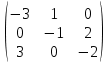 → →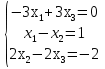 → →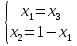 Пусть x1=x3=1, тогда x2=0. Таким образом, для получения μ' из μ требуется запустить по одному разу переходы t1 и t3, если это возможно. Замечание. Существование целого неотрицательного решения уравнения μ'=μ+xD является необходимым, но не достаточным условиемnдля достижимости μ'. В сети Петри (С, 0) допустима бесконечная последовательность запусков σ* тогда и только тогда, когда из μ0 достижима маркировка μ, из которой допустима повторяющаяся последовательность σ*. 53.Решение задачи сохранения с помощью матричного подхода. ПримерСП является сохраняющей тогда и только тогда, когда существует такой положительный вектор W, что выполняется DW=0. Пример: Дана СП. D= 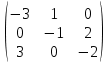 . Определить, является ли сеть сохраняющей по отношению к вектору. . Определить, является ли сеть сохраняющей по отношению к вектору.Решим систему уравнений DW=0.  → →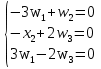 → → Система имеет множество решений. Пусть w2=3, тогда w1=1, w3=3/2. Таким образом, сеть является сохраняющей по отношению к вектору взвешивания W=(1, 3, 3/2). | |||||||||||||

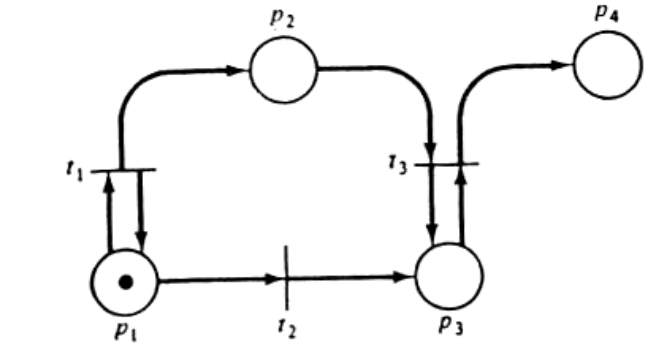

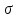 =(t1t1…t1) t2 (t3t3…t3).
=(t1t1…t1) t2 (t3t3…t3).  =(0, 14, 1, 7) достижима из начальной маркировки, однако она не покрывается, так как после получения
=(0, 14, 1, 7) достижима из начальной маркировки, однако она не покрывается, так как после получения