1. Понятие дискретной динамической системы
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
28. Свойства сетей Петри. Сохранение.Маркированная СП С=(P,T,I,O,μ0) - строго сохраняющая, если для всех μ'  R(C,μ0) выполняется условие: R(C,μ0) выполняется условие: 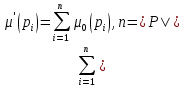 . .Так, число входов в каждый переход должно равняться числу выходов, |I(tj)|=|O(tj)|. Маркированная СП С=(P,T,I,O,μ0) - сохраняющая по отношению к вектору взвешивания w=(w1,w2,..,wn), n=|Р|, wi>0 для 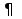 i, если для всех μ' i, если для всех μ' R(C,μ0) R(C,μ0) 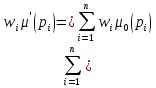 / /Строго сохраняющая сеть Петри является сохраняющей по отношению к w= (1,1,..,1). 29. Свойства сетей Петри. Активность.Пассивный (мертвый) переход – переход маркированной СП (C,μ0), который не является разрешенным ни в одной из достижимых маркировок, т.е. пассивный переход никогда не может быть запущен. Потенциально мертвый переход – переходt маркированной СП (C,μ0), который в процессе функционирования сети он может стать пассивным, т.е. может быть достигнута маркировка μ'  R(C,μ0) такая, что ни в одной из маркировок μ'' R(C,μ0) такая, что ни в одной из маркировок μ'' R(C,μ') переход t не разрешен. R(C,μ') переход t не разрешен.t-тупиковая маркировка – маркировка, в которой переход t является пассивным. Тупиковая маркировка в маркированной СП - маркировка, в которой не разрешен ни один переход. 30. Свойства сетей Петри. Асинхронность. Устойчивость. Параллелизм. Конфликтность.Все события СП считаются мгновенными, время их возникновения не учитывается. В СП анализируется только последовательность срабатывания переходов, т.е. причинно-следственные связи между отдельными действиями. Так СП учитывает асинхронность проектируемой системы. Переход tj  Т маркированной СП С=(P,T,I,O,μ0) - устойчивый, если для любой маркировки μ' Т маркированной СП С=(P,T,I,O,μ0) - устойчивый, если для любой маркировки μ' R(C,μ0), в которой переход tj разрешен и имеются другие разрешенные переходы, запуск любого из этих переходов не лишает возможности запуска перехода tj. R(C,μ0), в которой переход tj разрешен и имеются другие разрешенные переходы, запуск любого из этих переходов не лишает возможности запуска перехода tj.Маркированная СП устойчива, если устойчивы все ее переходы. Параллелизмом обладает СП, у которой в некоторой маркировке одновременно разрешены два или более переходов без общих входных позиций. Конфликтностью обладает сеть, у которой в некоторой маркировке разрешены два или более переходов с общими входными позициями. 31. Класс свободных языков сетей Петри.Функционирование СП можно описать в терминах последовательностей запусков переходов. Множество L(C) последовательностей запусков переходов СП C представляет подмножество множества T* всех слов в алфавите множества переходов T. Этот язык называют свободным языком СП. Множество свободных языков всех СП образует класс свободных языков LfСП. Ранее мы рассматривали СП, в которых все переходы считались различными. Однако, в системах, моделируемых СП, часто удобно считать различные события в некотором смысле одинаковыми. Например, одинаковые операторные блоки могут входить в различные части программы, одинаковые устройства могут быть встроены в разных частях конвейерной линии. Введем пометки, отмечающие «одинаковые» и «различные» переходы. Пометки являются символами некоторого алфавита А, а сеть в этом случае становится помеченной. Если символы переходов в последовательностях запусков заменить на помечающие символы, то свободный язык СП преобразуется в некоторый другой язык, порождаемый этой же сетью. В зависимости от правил пометки переходов и правил формирования последовательностей запусков переходов выделяются различные классы языков, порождаемых сетями Петри. |
