1. Понятие дискретной динамической системы
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
21. Правила выполнения сети Петри. Пример выполнения сети Петри.1. Если переход tj разрешен, то он может быть запущен, в результате маркировка μ заменяется на новую маркировку μ'. 2. Если два или более переходов, не имеющих общих входных позиций, разрешены, то они могут быть запущены в любой последовательности или параллельно. 3. Если два и более переходов разрешены в некоторой маркировке и имеют общие входные позиции, то запускается сначала один из них. При этом может оказаться, что запуск одного перехода лишает другой переход возможности запуска (конфликт). 4. Запуск переходов продолжается до тех пор, пока в СП не останется разрешенных переходов. Тогда сеть останавливается. Не исключено, что СП не останавливается. 22.Пространство состояний сети Петри. Функция следующего состоянияСостояние СП определяется ее маркировкой. Запуск перехода изменяет состояние сети Петри посредством изменения маркировки сети. Пространство состояний СП, обладающей n позициями, есть множество всех маркировок, т. е.N 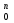 . . Изменение в состоянии μ, вызванное запуском перехода tj, определяется функцией следующего состояния: δ(μ,tj): N 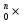 Т→ N Т→ N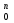 . δ(μ,tj)= . δ(μ,tj)=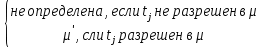 23.Две последовательности, описывающие выполнение сети Петри. Расширенная функция следующего состояния. Принцип монотонности.При выполнении сети Петри получаются две последовательности: последовательность маркировок (μ0,μ1,μ2,..) и переходов, которые были запущены σ=(tjo,tj1,tj2,..). Эти последовательности связаны соотношением: δ(μk,tjk)= μk+1 для k=0,1,2,.. Имея μ0 и σ, легко получить последовательность маркировок сети Петри. Наоборот, зная μ0 и последовательность маркировок, можно восстановить σ (Неоднозначность восстановления последовательности переходов может получиться, если два различных перехода имеют одинаковые комплекты входных и выходных позиций). Пусть имеется маркированная СП С=(P, T, I, O, μ0) и σ=(tjo, tj1, tj2,..). δ(μk,tjk)= μk+1 для k=0,1,2,.. Расширенная функция следующего состояния - это δ(μ0,σ)= δ(μ0, tjo, tj1, tj2, ...). Она определена только когда каждый из переходов в разрешен к моменту запуска. Принцип монотонности: пусть имеются две маркировки некоторой сети. Отношение μ" 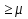 ' истинно, если каждый элемент маркировки μ" не меньше соответствующего элемента маркировки μ'. Тогда все последовательности запусков, допустимые в СП с μ') допустимы также в CП с μ'' (т.е. увеличение вектора маркировки влечет за собой увеличение числа допустимых последовательностей запусков). ' истинно, если каждый элемент маркировки μ" не меньше соответствующего элемента маркировки μ'. Тогда все последовательности запусков, допустимые в СП с μ') допустимы также в CП с μ'' (т.е. увеличение вектора маркировки влечет за собой увеличение числа допустимых последовательностей запусков).24. Достижимая маркировка. Непосредственно достижимая маркировка. Множество достижимости сети Петри. Пример.Для маркированной СП С=(P, T, I, O, μ) маркировка μ' называется непосредственно достижимой из μ, если существует переход tj  Т, такой, что δ(μ,tj)=μ'. Т, такой, что δ(μ,tj)=μ'.Маркировка μ* достижима из маркировки μ, если существует последовательность маркировок с начальной маркировкой μ и конечной μ*, в которой каждая последующая маркировка непосредственно достижима из предыдущей. Множество достижимости R(C,μ0) маркированной СП (C,μ0) - множество всех маркировок, достижимых из μ0. Маркировка 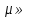 R(C,μ0), если существует какая-либо последовательность запусков переходов, изменяющих μ0 на μ. R(C,μ0), если существует какая-либо последовательность запусков переходов, изменяющих μ0 на μ.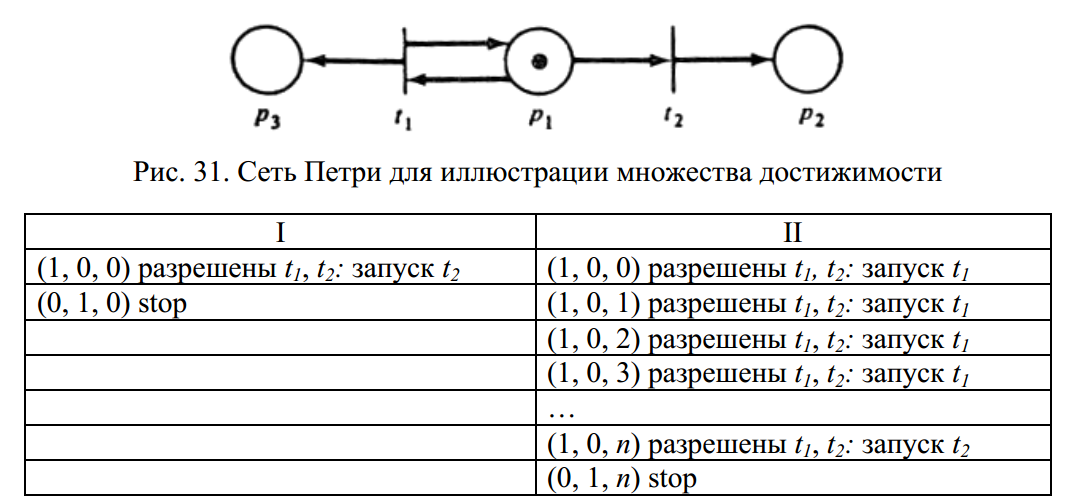 |
