1. Понятие дискретной динамической системы
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
17. Структура сетей Петри. Граф сети Петри.Сеть Петри - это четверка С=(P, T, I, O), где Р={p1, p2, .., pn} – конечное множество условий (позиций), |P|=n, n≥0; Т={t1, t2, .., tm} – конечное множество событий (переходов), |Т|=m, m≥0; I: T→Р∞ – входная функция – отображение переходов в комплекты входных позиций, I(tj) интерпретируется как комплект входных позиций для перехода tj; О: T→Р∞ – выходная функция – отображение переходов в комплекты выходных позиций, О(tj) интерпретируется аналогично. Связь м/у условиями и событиями отображаются в графе СП, с двумя типами вершин: кружочки (позиции) соответствуют условиям, палочки (переходы) - событиям. Граф СП-двудольный ориентированный мультиграф (может иметь кратные дуги) G=(V,A), где V=P 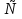 T={v1,v2,..,vr} – множество вершин, А={a1,a2,...,as}–комплект дуг.. T={v1,v2,..,vr} – множество вершин, А={a1,a2,...,as}–комплект дуг..18.Маркировка СП. Маркированная СП. Расширенная входная функция. Расширенная выходная функция.Маркировка СП С=(P, T, I, O) - функция, отображающая множество позиций Р в множество неотрицательных целых чисел, которые представляют количество фишек в позиции: μ: P→N0. Если μ(pi)=0 то условие pi не выполнено; если (pi)=1, то - выполнено; если μ(pi)=n>1(n фишек), то условие выполнено с n-кратным запасом. Маркировку представляют: μ=(μ1, μ2,..,μn), где n=|P|, μi – целое неотрицательное число, равное количеству фишек, принадлежащих позиции pi (t=1, 2,.., n). Маркированная СП М=(Р, Т, I, О, μ)- СП С=(P, T, I, O) с маркировкой μ. Для СП существует бесконечно много маркировок. Расширенная входная функция СП – отображение позиций в комплекты переходов на входе I’: Р→T∞, а расширенная выходная функция –отображение позиций в комплекты переходов на выходе О’: Р→T∞, такие, что: #(tj,I’(pi))=#(pi,O(tj)), #(tj,O’(pi))=#(pi,I(tj)). 19. Двойственная сеть Петри. Пример. Инверсная сеть Петри. Пример.Двойственной к СП С=(P, T, I, O) является СП С*=(T, P, I, O), которая получается из сети С в результате перестановки местами позиций и переходов. При переходе к двойственной СП структура графа сохраняется, просто меняются местами позиции и переходы. 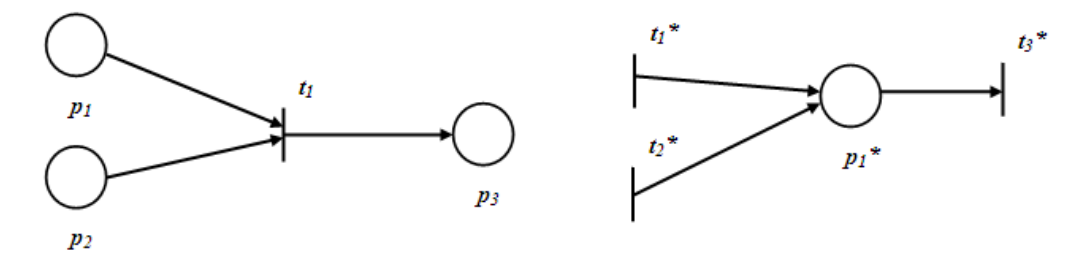 Инверсной к СП С=(P, T, I, O) является СП 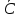 , которая получается из С путем изменения ориентации каждой дуги на противоположную: , которая получается из С путем изменения ориентации каждой дуги на противоположную: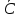 =(P, T, O, I). =(P, T, O, I).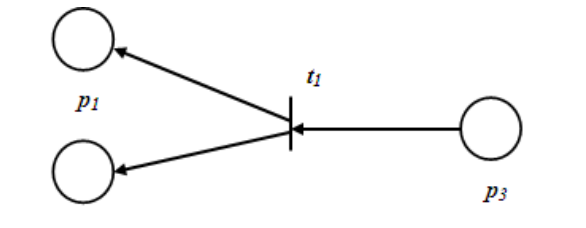 20. Функционирование сетей Петри. Схема изменения маркировки позиции pi в результате запуска перехода tj.Маркированная СП выполняется посредством запусков переходов. Переход запускается удалением фишек из его входных позиций и добавлением фишек в его выходные позиции. Переход может запускаться только в том случае, когда он разрешен. Переход tj в маркированной СП С=(P,T,I,O,μ) разрешен, если  рi рi Р μ(pi) Р μ(pi) # pi, I(tj)).(То есть переход tj разрешен, если каждая из его входных позиций имеет число фишек, не меньшее числа дуг из этой позиции в tj. Если переход не имеет входных позиций, то он всегда разрешен). # pi, I(tj)).(То есть переход tj разрешен, если каждая из его входных позиций имеет число фишек, не меньшее числа дуг из этой позиции в tj. Если переход не имеет входных позиций, то он всегда разрешен).В результате запуска перехода из его входных позиций удаляются фишки по одной для каждой дуги, ведущей из позиции в переход, и добавляются фишки в выходные позиции перехода – по одной для каждой дуги. В результате запуска разрешенного перехода tj образуется новая маркировка μ', причем для  pi pi P: μ'(pi)=μ(pi) – #(pi,I(tj))+ #(pi,O(tj)). P: μ'(pi)=μ(pi) – #(pi,I(tj))+ #(pi,O(tj)). |
