1. Понятие дискретной динамической системы

• Название: 1. Понятие дискретной динамической системы
• Дата: 23.11.2018
• Размер: 0.51 Mb.
• Имя файла: tmp_4118-Otvety_k_ekzamenu_po_predmetu_Teoria_vychislitelnykh_pr.docx
• Тип: Документы; #57412
• страница: 14 из 15

41.Средства ограничения дерева достижимости до определенных (конечных) размеров.

На практике при использовании ДД для анализа СП, естественно, ограничивают его до конечных размеров. Назовем такое ДД усеченным.

В первую очередь, введем символ ω, который будет обозначать неограниченное число фишек в позиции и ω + а = ω, ω – a = ω , а< ω, где а – целое неотрицательное число.

Пусть имеется маркированная СП (P,T,I,O,μ₀), х – вершина ДД, µ[х] – маркировка, соответствующая вершине х ДД. Обозначим через µ[х]_i число фишек в позиции p_i∈ P для маркировки μ[х]. Тогда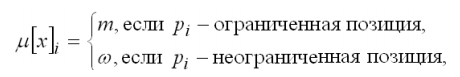



где m – целое неотрицательное число.

Расширенным множеством натуральных чисел будем называть множество натуральных чисел, дополненное символом ω .

Во вторую очередь, естественно не строить исходящих дуг для терминальных и дублирующих вершин.

42. Алгоритм построения дерева достижимости.

Пусть х₀– граничная вершина. Строится дерево: в ширину, вершины уровня обрабатывают слева направо. Алгоритм работает пока имеются граничные вершины.

1. Если для µ[x] ни один из переходов не разрешен, то х – терминальная вершина.

2. Если в построенной части дерева имеется вершина у≠x, для которой µ[x]= µ[y], то вершина х – дублирующая.

3. Если х – нетерминальная и недублирующая, то существует дуга из вершины х, помеченная t_jи ведущая в вершину z.

Маркировка µ[z] определяется для каждой позиции р_i следующим образом:

а) если µ[х]_i= ω, то µ[z]_i=ω.

б) если на пути от корневой вершины к х существует вершина y:

µ[y]< δ( [x], t_j) и µ[y]_i < δ( µ[x], t_j)_i , то µ[z]_i = ω.

в) Во всех остальных случаях µ[z]_i= δ(µ[x],t_j)_i.

После обработки вершина х становится внутренней, а z – граничной. Когда все вершины становятся дублирующими либо терминальными либо внутренними, работа алгоритма завершается.

Замечание 1. Алгоритм построения усеченного дерева достижимости позволяет установить в сети наличие пассивных переходов и позиций. Если ни одна из дуг дерева достижимости не помечена названием данного перехода, то он пассивный. Если некоторая позиция во всех вершинах дерева достижимости имеет ноль фишек, то позиция – пассивная.

Замечание 2. В процессе построения усеченного ДД использование символа ω приводит к потере информации о том, какие именно значения может принимать количество фишек в позиции, известно лишь, что это число потенциально сколь угодно большое. Следствием этого является невозможность применения усеченного ДД для решения задач достижимости и покрываемости, если маркировки его вершин содержат символ ω.

Замечание 3. Еще одним важным свойством алгоритма построения усеченного ДД является то, что он заканчивает работу за конечное число шагов. Доказательство этого свойства алгоритма основано на трех леммах.

43. Лемма 1 для доказательства теоремы о конечности дерева достижимости сети Петри.

Лемма 1. Во всяком корневом ориентированном бесконечном дереве, в котором каждая вершина имеет конечное число непосредственно последующих вершин, существует бесконечный путь, исходящий из корня.

Доказательство.

Начнем с корня х₀. Поскольку эта вершина имеет конечное число непосредственно последующих вершин, то найдется одна или более вершин, непосредственно следующих за х₀и являющаяся корнем бесконечного поддерева. Пусть это будет вершина x₁. Повторяя рассуждения, получим х₂и т.д. Получим х₀, х₁,x₂, x₃, ... – бесконечный путь, исходящий из корня.