Ответы на экзамен по Линейной алгебре. ответы на экзамен по Линейной Алгебре. 1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами умножение на число, сложение, умножение матриц

• Название: 1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами умножение на число, сложение, умножение матриц
• Анкор: Ответы на экзамен по Линейной алгебре
• Дата: 22.01.2023
• Размер: 2.37 Mb.
• Имя файла: ответы на экзамен по Линейной Алгебре.doc
• Тип: Решение; #898154
• страница: 2 из 10

Определители и их свойства

Понятие определителя - число, характеризующее квадратную матрицу , необходимо для решения систем линейных алгебраических уравнений.

Определитель матрицы обозначают , , .

1) Определителем матицы 1-го порядка , называется элемент : ;

2) Определителем матрицы 2-го порядка называется число, вычисляемое по формуле: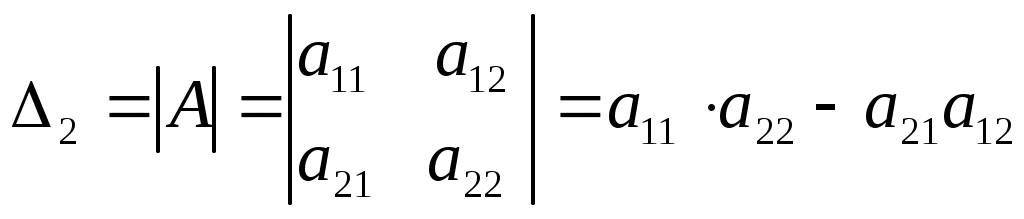

. Произведения называются членами определителя 2-го порядка.

Пример. Вычислить определитель матрицы . Р е ш е н и е. .

3) Определителем матрицы 3-го порядка называется число, вычисляемое по формуле: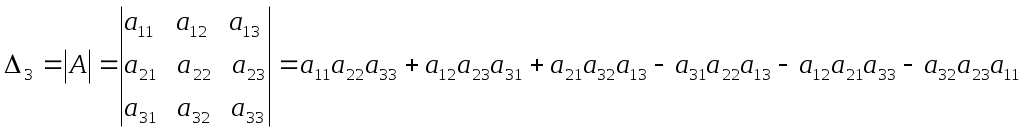

.

Данная формула получила название правила треугольников или правило Сарруса.

При вычислении определителя 3-го порядка удобно пользоваться следующей схемой, показывающей произведения каких элементов берутся со знаком “+”, а каких со знаком “-“:

П
ример. Вычислить определитель . Р е ш е н и е. .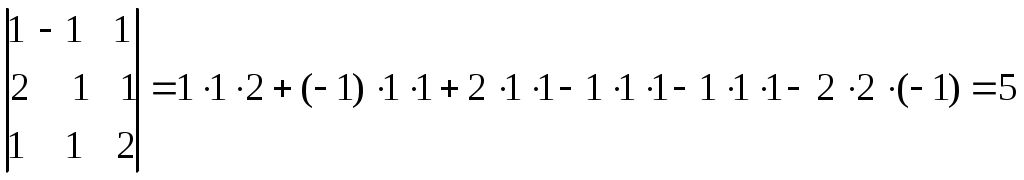

4) Определитель квадратной матрицы -го порядка (определитель -го порядка).

Рассмотрим квадратную матрицу n-го порядка. Зачеркнем элемент матрицы, стоящий на пересечении 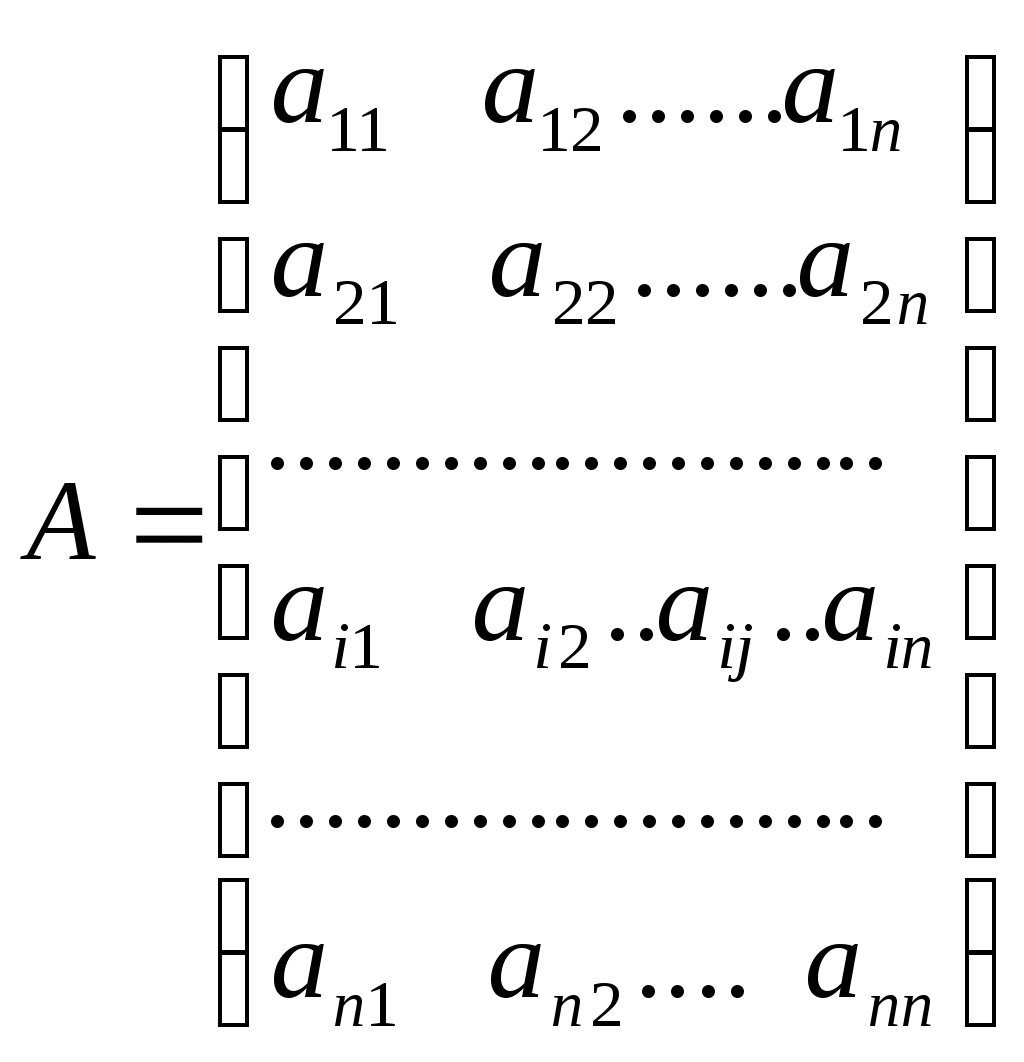-й строки и -го столбца. В результате получается матрица порядка . Пусть дана матрица n-го порядка:

.

Минором элемента матрицы n-го порядка называется определитель матрицы -го порядка, полученной из матрицы вычеркиванием -й строки и -го столбца.

Н апример минором матрицы 3-го порядка будет:

Определение. Алгебраическим дополнением элемента матрицы -го порядка называется минор, взятый со знаком :

.

Пример. Найти алгебраические дополнения всех элементов матрицы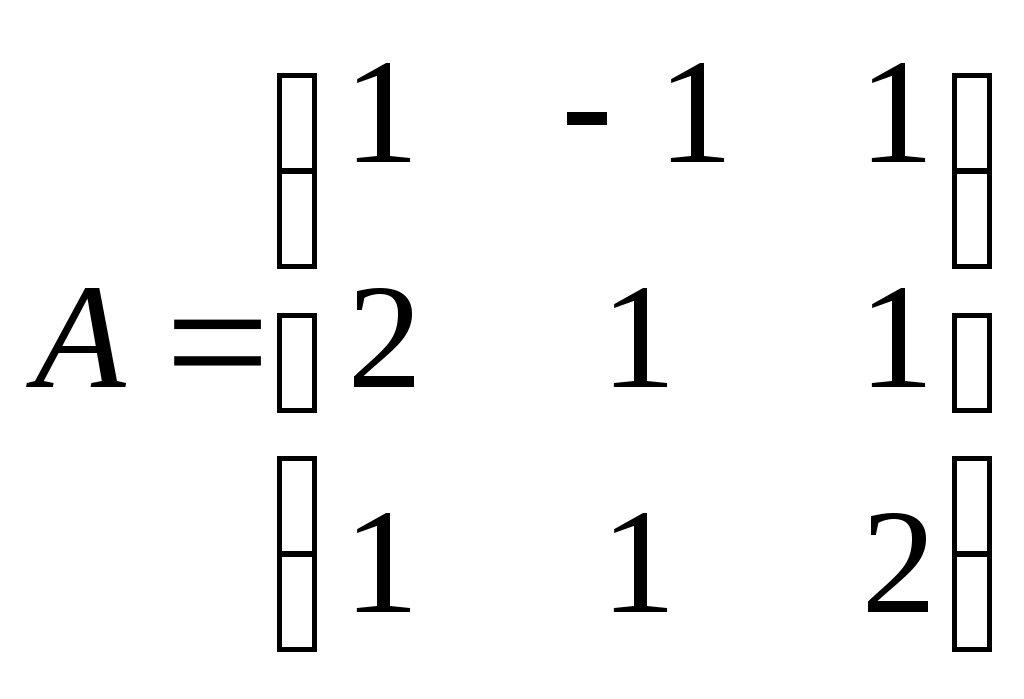

.

Р е ш е н и е:

,	,	,
,	,	,

Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

(разложение по элементам -й строки; ).



(разложение по элементам -го столбца; ).

Пример. Вычислить определитель 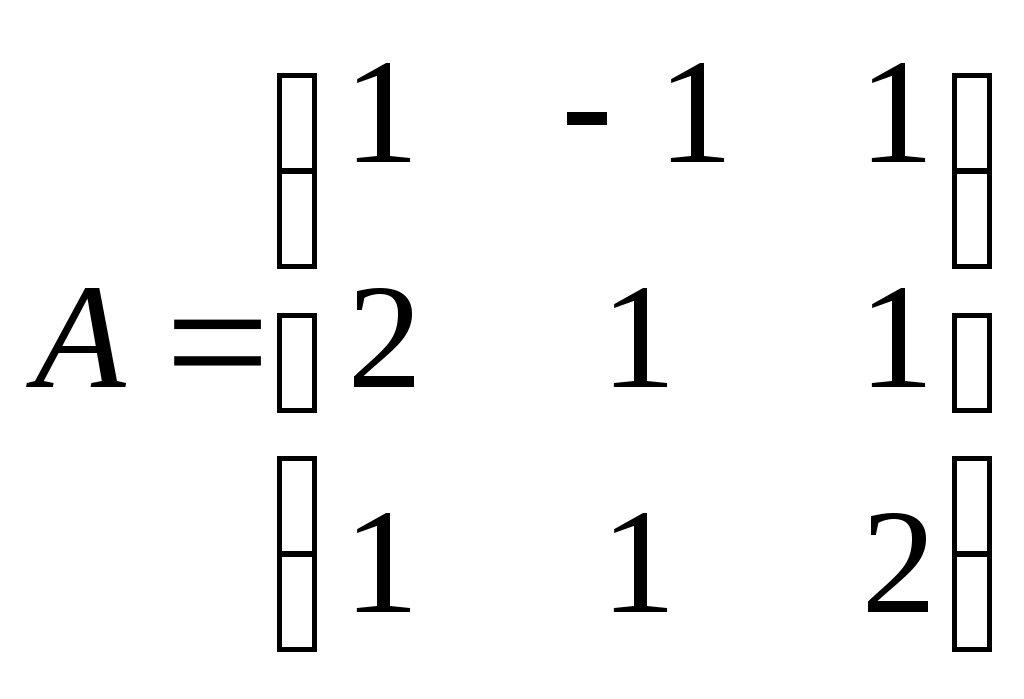разложением по элементам

а) 1-й строки; б) 1-го столбца.

Р е ш е н и е. а) , б) .