Ответы на экзамен по Линейной алгебре. ответы на экзамен по Линейной Алгебре. 1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами умножение на число, сложение, умножение матриц
 Скачать 2.37 Mb. Скачать 2.37 Mb.
|
|
1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами: умножение на число, сложение, умножение матриц. О 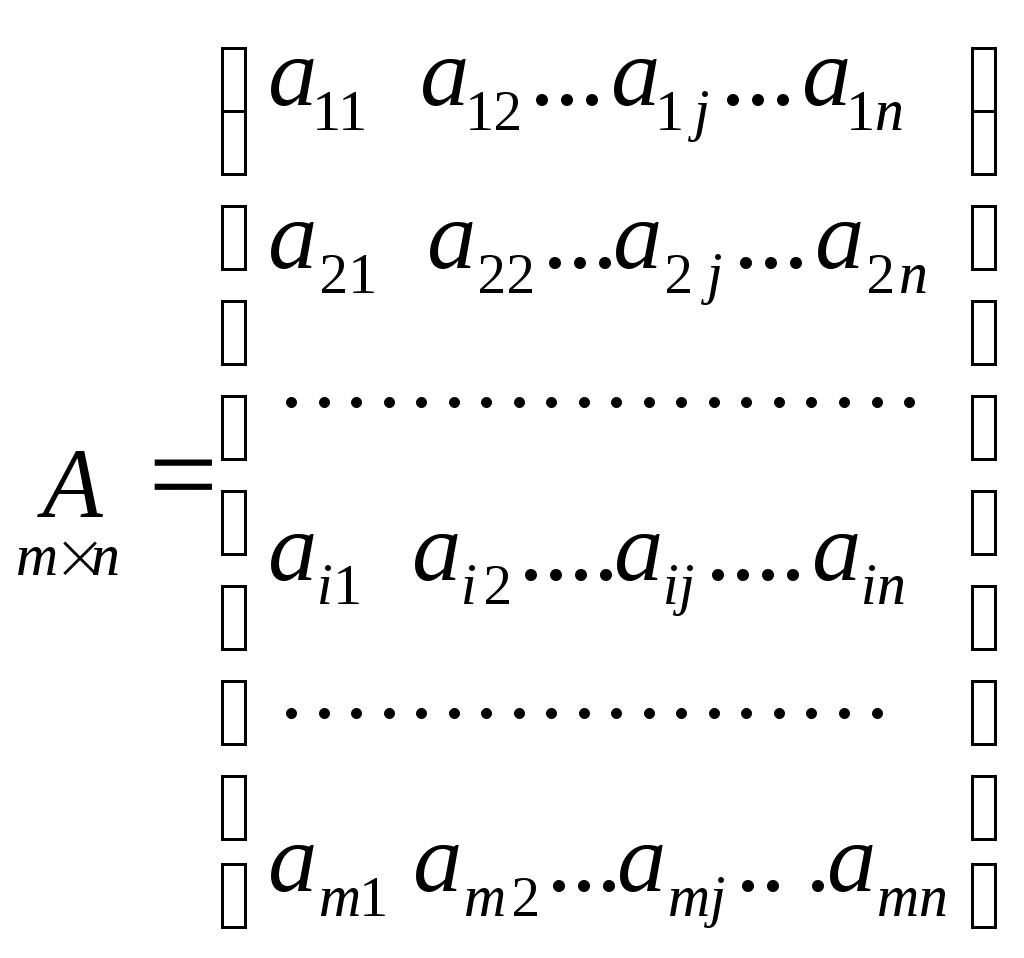 пределение. Матрицей размера называется прямоугольная таблица, содержащая m строк и n столбцов. пределение. Матрицей размера называется прямоугольная таблица, содержащая m строк и n столбцов.Матрицы широко применяются для описания экономических объектов и процессов. Элементами матрицы могут быть числа, буквы (символы) и другие объекты. Матрицы обозначают прописными (заглавными) буквами A, B, C, …, элементы матрицы – строчными буквами с двойной индексацией aij, где i - номер строки, j - номер столбца: Виды матриц: 1) Матрица-строка: ; 2) Матрица-столбец: ; 3) Нулевая матрица: ; 4) Квадратная матрица – если (например n = 2): ; 5) Диагональная матрица (напр. 3-го порядка, где любые числа ): ; 6) Единичная матрица (например, 3-го порядка) 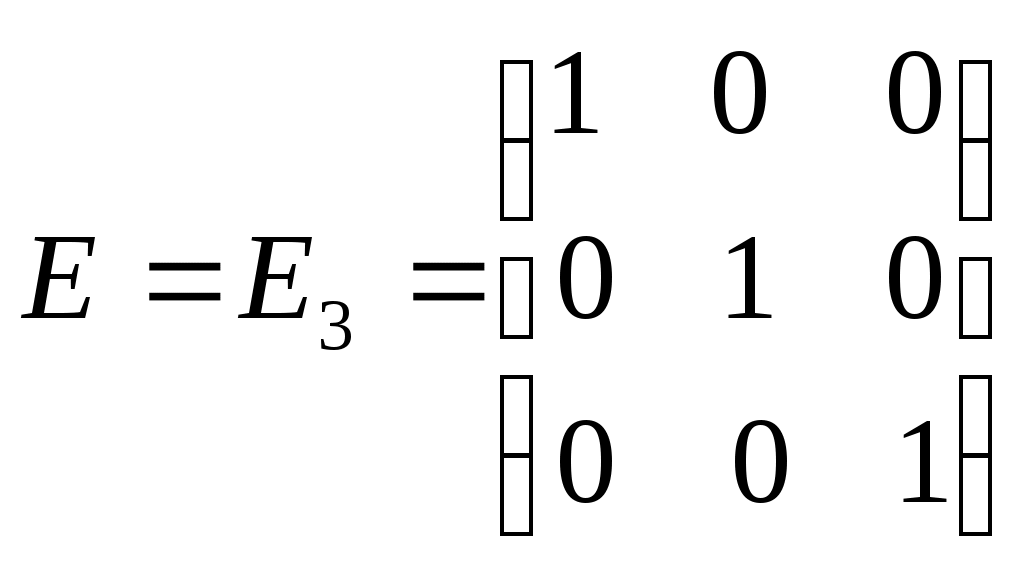 Операции над матрицамиУмножение матрицы на число. Произведением матрицы A на число называется матрица ,элементы которой для Пример. Вычислить , если . Р е ш е н и е: . Если Сложение матриц. Суммой матриц Пример. Вычислить С = А + В, если . Р е ш е н и е: . Вычитание матриц. Разность матриц одинакового размера определяется как Умножение матриц. Умножение матрицы Пример. Вычислить произведение матриц 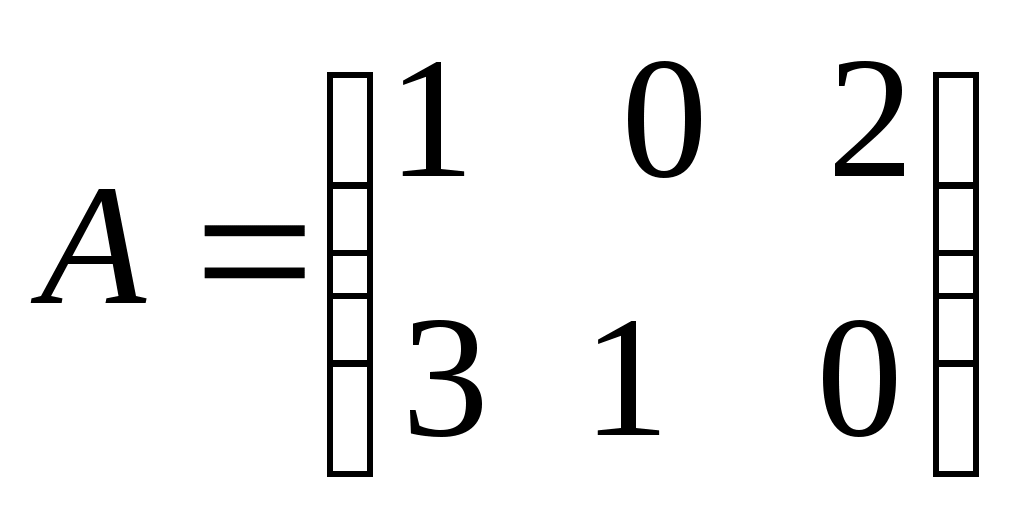 , , 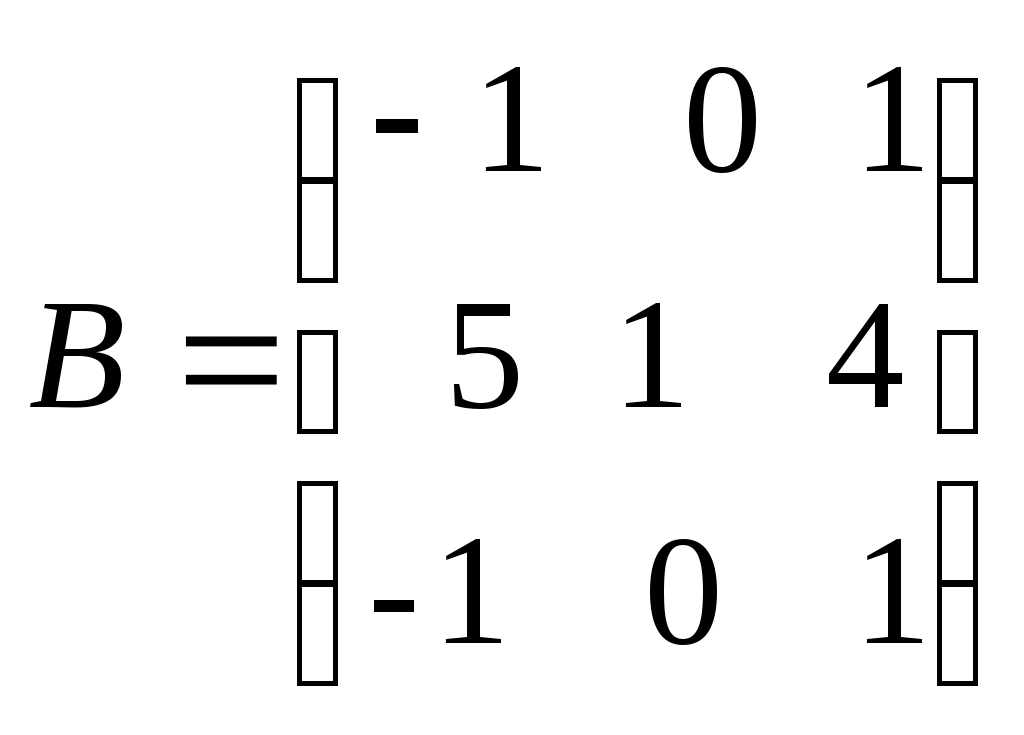 . .Р е ш е н и е. Найдем размер матрицы произведения 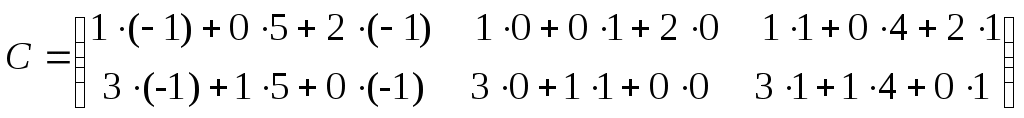 = =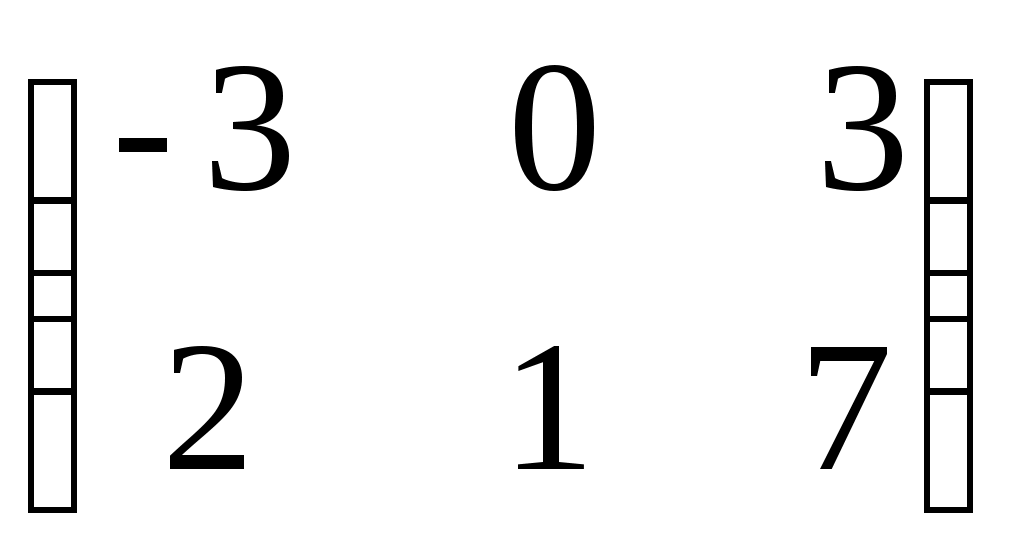 . .Свойства операций сложения и умножения матриц 8) 9) 10) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. если Пример. 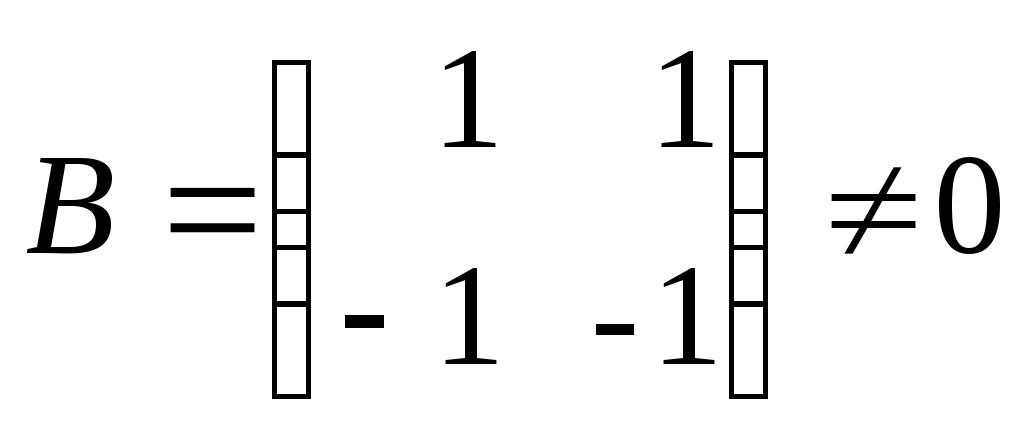 , но , но 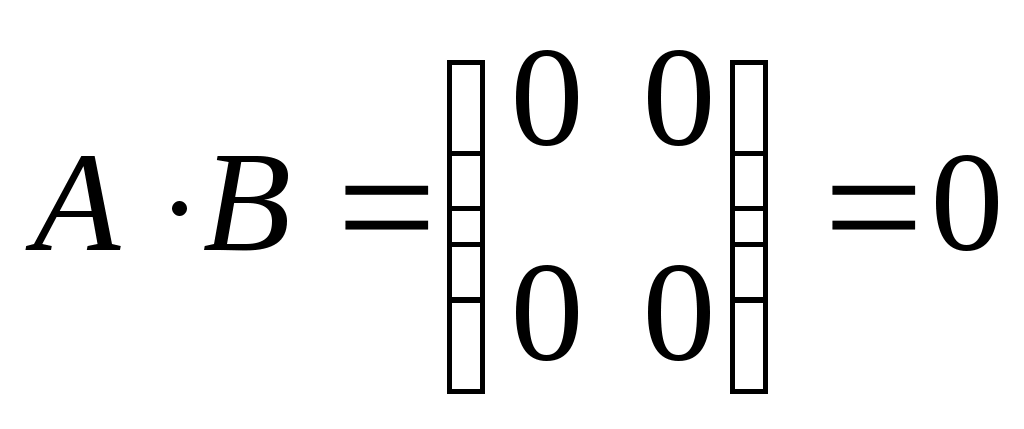 . .Возведение в степень. Целой положительной степенью Транспонирование матриц. Транспонирование матрицы есть переход матрицы 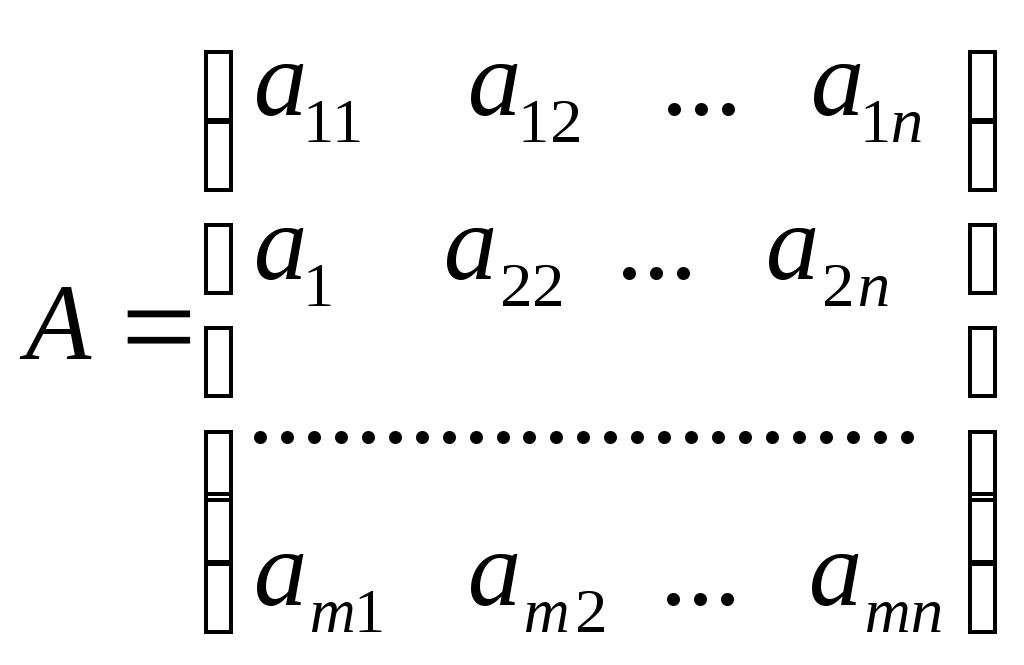 , , 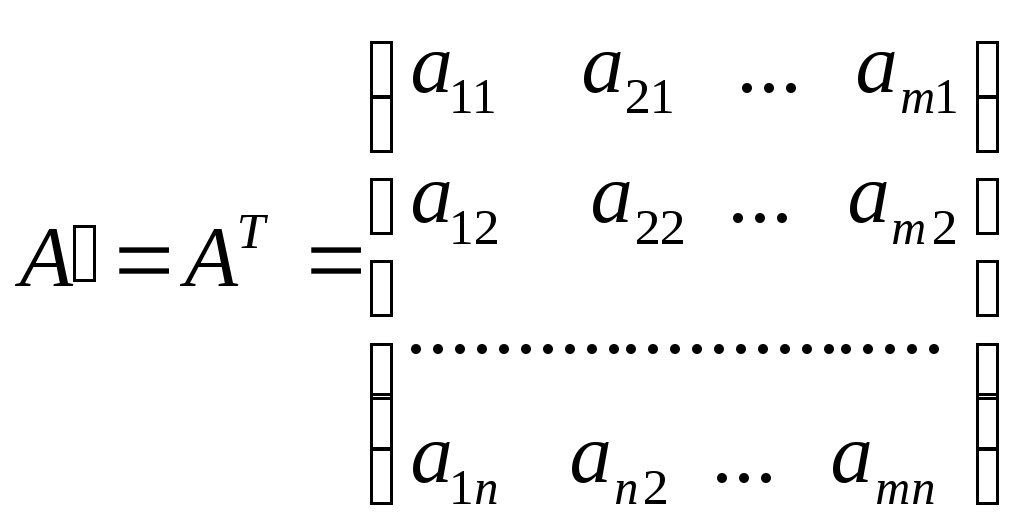 , ,т.е. если Свойства операции транспонирования. 2. Определители 2, 3 и n-го порядков (определения и их свойства). Теорема Лапласа о разложении определителя по элементам строки или столбца. |
