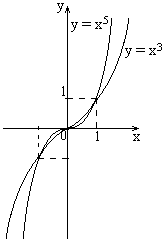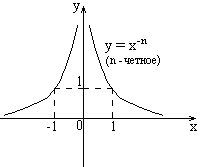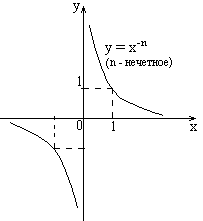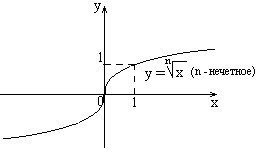Ответы на экзамен по Линейной алгебре. ответы на экзамен по Линейной Алгебре. 1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами умножение на число, сложение, умножение матриц
 Скачать 2.37 Mb. Скачать 2.37 Mb.
|
Линейная независимость строк матрицыДана матрица 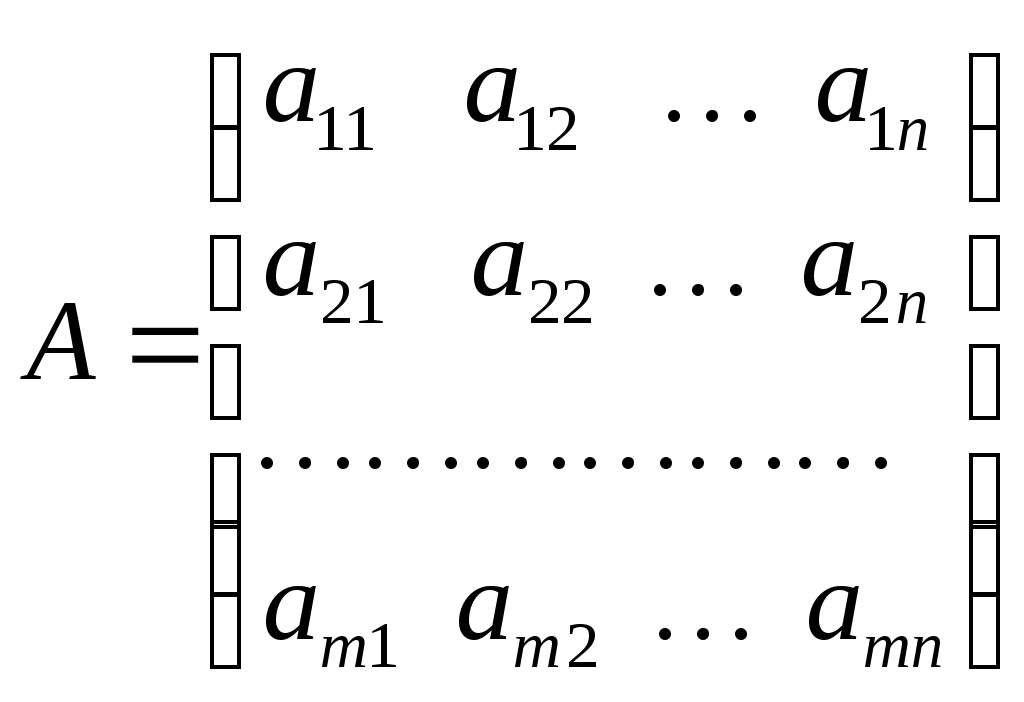 Обозначим строки матрицы следующим образом: 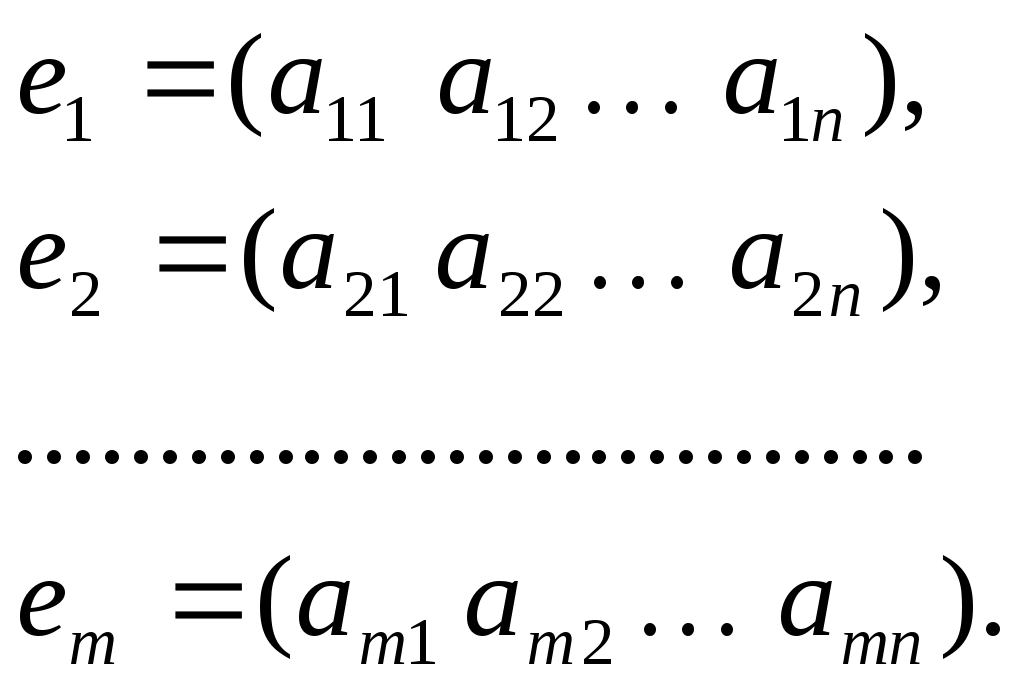 Две строки называются равными, если равны их соответствующие элементы. . Введем операции умножения строки на число и сложение строк как операции, проводимые поэлементно: Определение. Строка называется линейной комбинацией строк Определение. Строки матрицы , где Линейная зависимость строк матрицы обозначает, что хотя бы 1 строка матрицы является линейной комбинацией остальных. Определение. Если линейная комбинация строк (1.1) равна нулю тогда и только тогда, когда все коэффициенты Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные строки (столбцы). Теорема играет принципиальную роль в матричном анализе, в частности, при исследовании систем линейных уравнений. 6. Векторы. Операции над векторами (сложение, вычитание, умножение на число), n-мерный вектор. Понятие о векторном пространстве и его базисе. В  ектором назевается направленный отрезок с начальной точкой А и конечной точкой В (который можно перемещать параллельно самому себе). ектором назевается направленный отрезок с начальной точкой А и конечной точкой В (который можно перемещать параллельно самому себе).Векторы могут обозначаться как 2-мя прописными буквами, так и одной строчной с чертой или стрелкой. Длиной (или модулем) вектора называется число, равное длине отрезка АВ, изображающего вектор. Векторы, лежащие на одной прямой или на параллельных прямых, называют коллинеарными. Если начало и конец вектора совпадают ( ), то такой вектор называется нулевым и обозначается = . Длина нулевого вектора равна нулю: = 0. Произведением вектора на число : Будет вектор, имеющий длину , направление которого совпадает с направлением вектора , если , и противоположно ему, если . Противоположным вектором - называется произведение вектора - на число (-1), т.е. - = . Суммой двух векторов и называется вектор , начало которого совпадает с началом вектора , а конец с концом вектора , при условии, что начало совпадает с концом . (правило треугольников). Аналогично определяется сумма нескольких векторов. Разностью двух векторов и называется сумма вектора и вектора - , противоположного . Скалярное произведение Определение: Скалярным произведение двух векторов и называется число, равное произведению длин этих векторов на косинус угла между ними: n-мерный вектор и векторное пространство Определение. n-мерным вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде х = (х1,х2,…,хn), где хi – i-я компонента вектора х. Понятие n-мерного вектора широко используется в экономике, например, некоторый набор товаров можно охарактеризовать вектором х = (х1,х2,…,хn), а соответствующие цены у = (у1,у2,…,уn). - Два n-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е. х=у, если хi = уi, i = 1,2,…,n. - Суммой двух векторов одинаковой размерности n называется вектор z = x + y, компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е. zi = xi + yi, i = 1,2,…,n. - Произведением вектора х на действительное число называется вектор , компоненты которого равны произведению на соответствующие компоненты вектора , т.е. , i= 1,2,…,n. Линейные операции над любыми векторами удовлетворяют следующим свойствам: 1) - коммутативное (переместительное) свойство суммы; 2) - ассоциативное (сочетательное) свойство суммы; 3) - ассоциативное относительно числового множителя свойство; 4) - дистрибутивное (распределительное) относительно суммы векторов свойство; 5) - дистрибутивное относительно суммы числовых множителей свойство; 6) Существует нулевой вектор такой, что для любого вектора (особая роль нулевого вектора); 7) Для любого вектора существует противоположный вектор такой, что ; 8) для любого вектора (особая роль числового множителя 1). Определение. Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее приведенным выше восьми свойствами (рассматриваемым как аксиомы), называется векторным состоянием. Размеренность и базис векторного пространства Определение. Линейное пространство называется n-мерным, если в нем существует n линейно независимых векторов, а любые из векторов уже являются зависимыми. Другими словами, размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов. Число n называется размерностью пространства и обозначается . Совокупность n линейно независимых векторов n-мерного пространства называется базисом. Собственные векторы и собственные значения матрицы. Характеристическое уравнение матрицы. Определение. Вектор называется собственным вектором линейного оператора , если найдется такое число , что: Число называется собственным значением оператора (матрицы А), соответствующим вектору . Можно записать в матричной форме: , где - матрица-столбец из координат вектора , или в развернутом виде: Перепишем систему так, чтобы в правых частях были нули:   или в матричном виде: . Полученная однородная система всегда имеет нулевое решение. Для существования ненулевого решения необходимо и достаточно, чтобы определитель системы: . или в матричном виде: . Полученная однородная система всегда имеет нулевое решение. Для существования ненулевого решения необходимо и достаточно, чтобы определитель системы: .Определитель является многочленом n-й степени относительно . Этот многочлен называется характеристическим многочленом оператора или матрицы А, а полученное уравнение – характеристическим уравнением оператора или матрицы А. Пример: Найти собственные значения и собственные векторы линейного оператора , заданного матрицей . Р е ш е н и е: Составляем характеристическое уравнение или , откуда собственное значение линейного оператора . Находим собственный вектор , соответствующий собственному значению . Для этого решаем матричное уравнение: или , или , откуда находим: , или , или . Предположим, что , получим, что векторы , при любом являются собственными векторами линейного оператора с собственным значением . Аналогично, вектор . 8. Система п линейных уравнений с п переменными (общий вид). Матричная форма записи такой системы. Решение системы (определение). Совместные и несовместные, определенные и неопределенные системы линейных уравнений. Решение системы Системы линейных уравнений находят широкое применение в экономике. Система 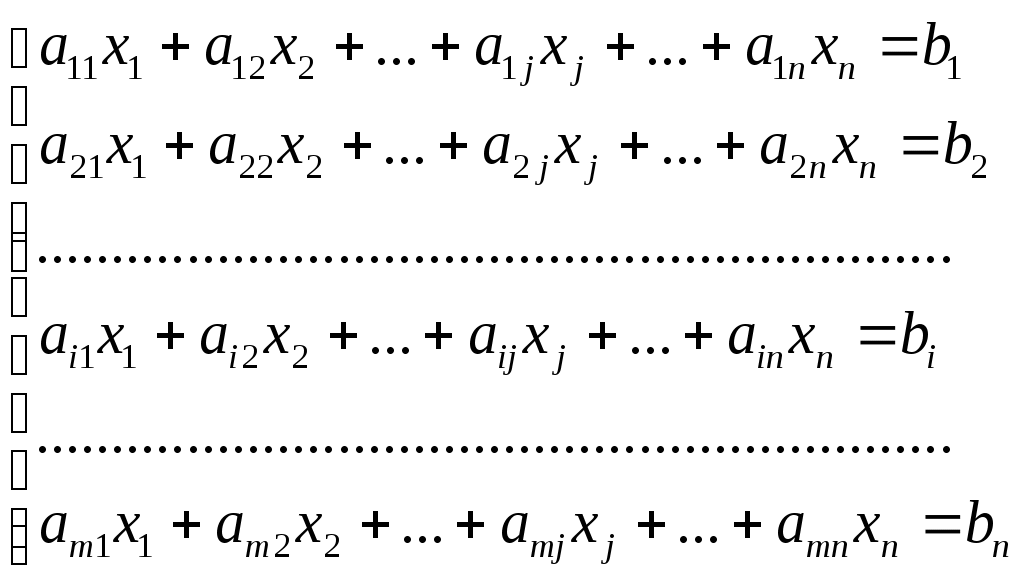 , ,где Краткая запись: Определение. Решением системы называется такая совокупность значений Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. Две системы уравнений называются равносильными (эквивалентными), если они имеют одно и то же множество решений (например, одно решение). Запишем систему в матричной форме: Обозначим: , где А – матрица коэффициентов при переменных, или матрица системы, Х – матрица-столбец переменных, В – матрица-столбец свободных членов. Т.к. число столбцов матрицы равно числу строк матрицы , то их произведение: Есть матрица-столбец. Элементами полученной матрицы являются левые части начальной системы. На основании определения равенства матриц начальную систему можно записать в виде: . Теорема Крамера. Пусть Пример. Решить систему уравнений по формулам Крамера 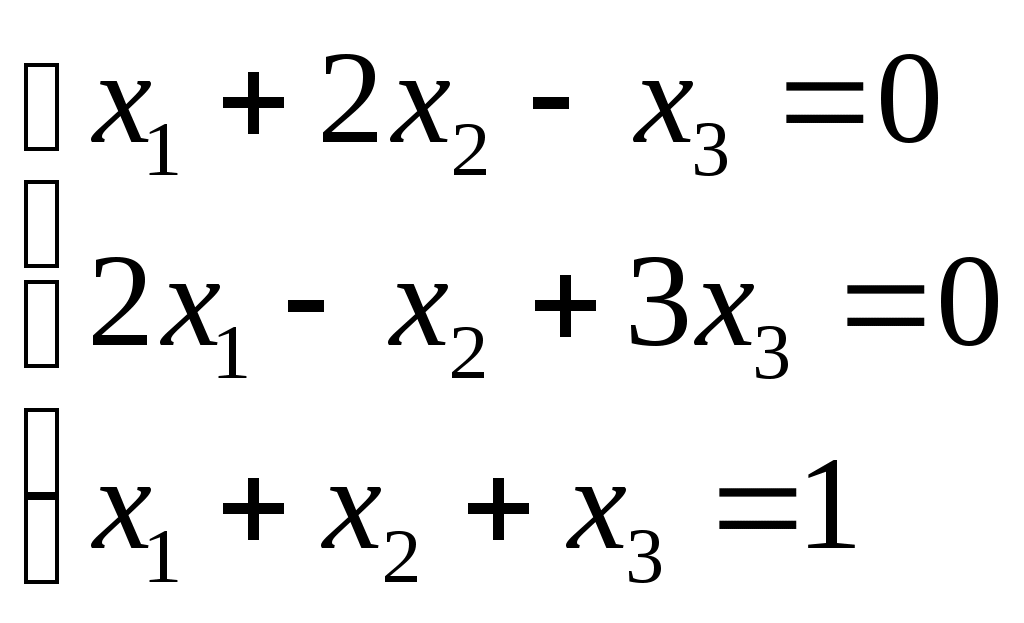 Р е ш е н и е. Определитель матрицы системы 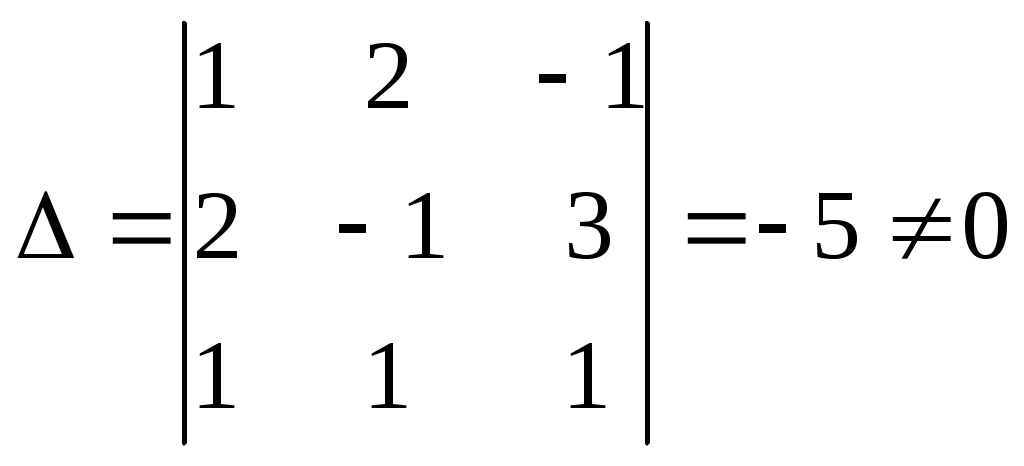 . Следовательно, система имеет единственное решение. Вычислим . Следовательно, система имеет единственное решение. Вычислим 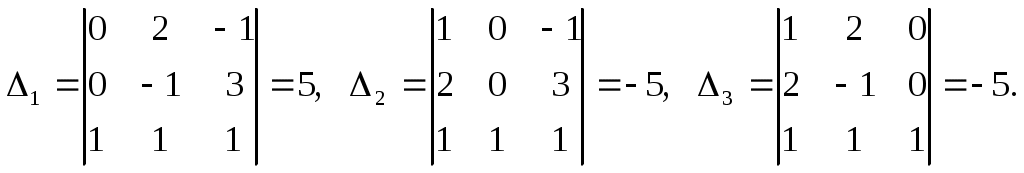 По формулам Крамера: 9. Метод Гаусса решения системы n линейных уравнений с п переменными. Понятие о методе Жордана – Гаусса. Метод Гаусса - метод последовательного исключения переменных. Метод Гаусса заключается в том, что с помощью элементарных преобразований строк и перестановок столбцов система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Преобразования Гаусса удобно проводить не с самими уравнениями, а с расширенной матрицей их коэффициентов 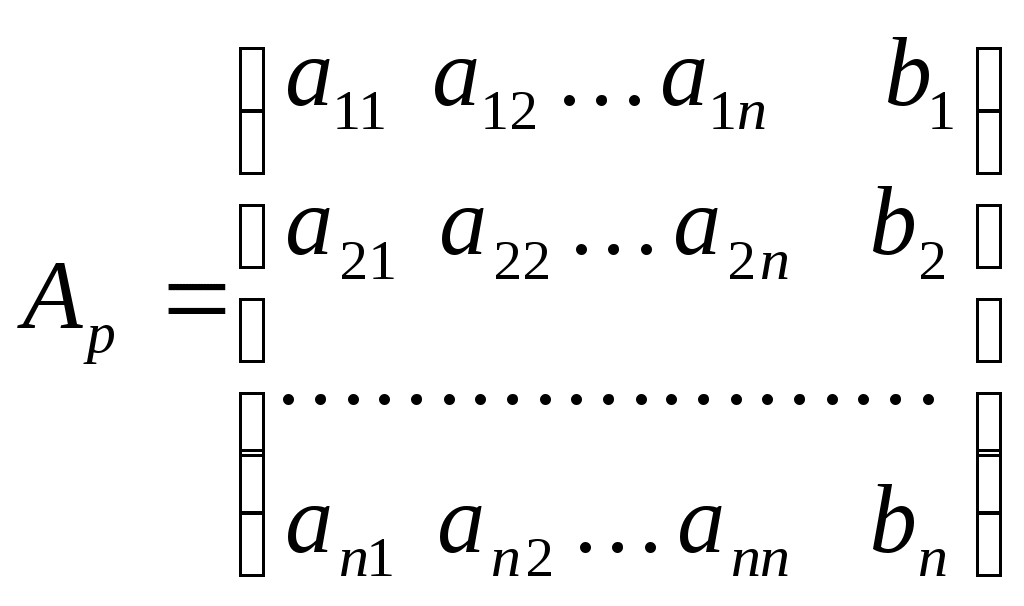 . .Следует отметить, что методом Гаусса можно решить любую систему уравнений вида 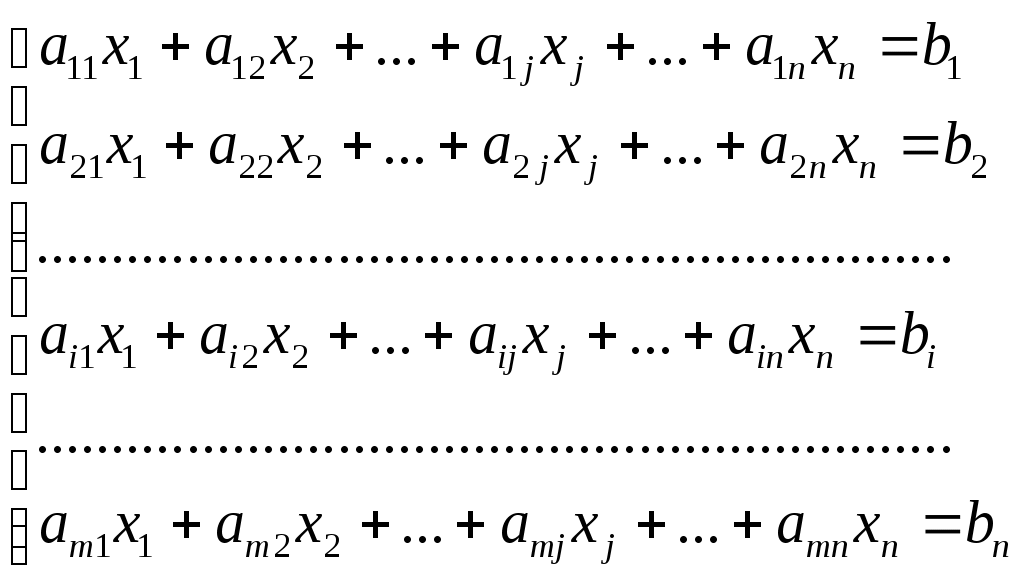 . .Пример. Методом Гаусса решить систему: 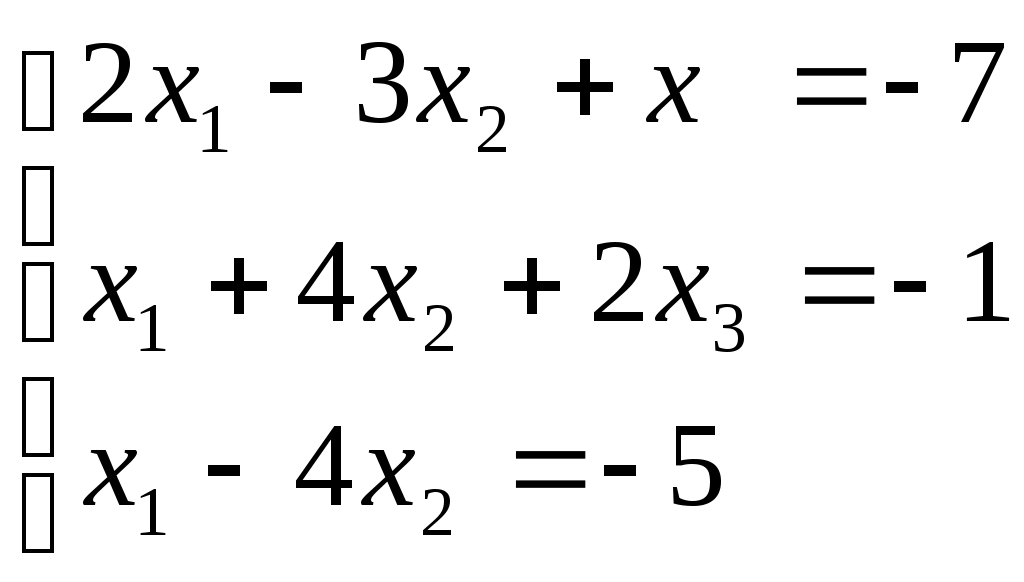 Выпишем расширенную матрицу системы. Шаг 1. Поменяем местами первую и вторую строки, чтобы Шаг 2. Умножим элементы первой строки на (–2) и (–1) и прибавим их к элементам второй и третьей строк, чтобы под элементом Шаг 3. Умножим элементы третьей строки на (–0,5). Шаг 4. Поменяем местами вторую и третью строки. Шаг 5. Поменяем местами второй и третий столбец. (Шаги 3, 4, 5 приведены с тем, чтобы Шаг 6. Элементы второй строки умножим на 3 и прибавим их к элементам третьей строки, тогда под элементом 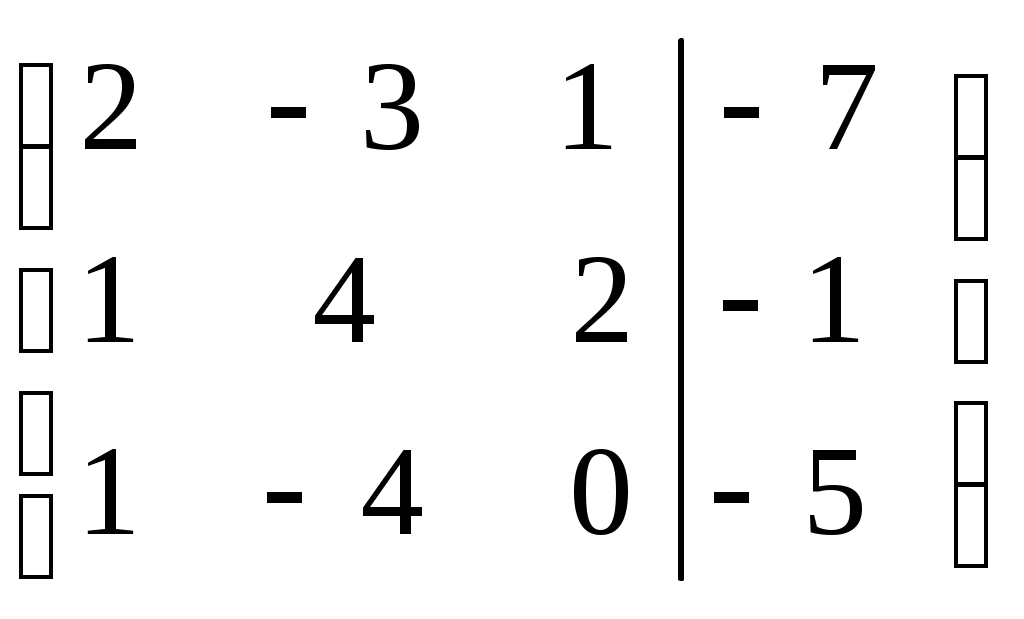 (называется расширенная матрица системы) (называется расширенная матрица системы) 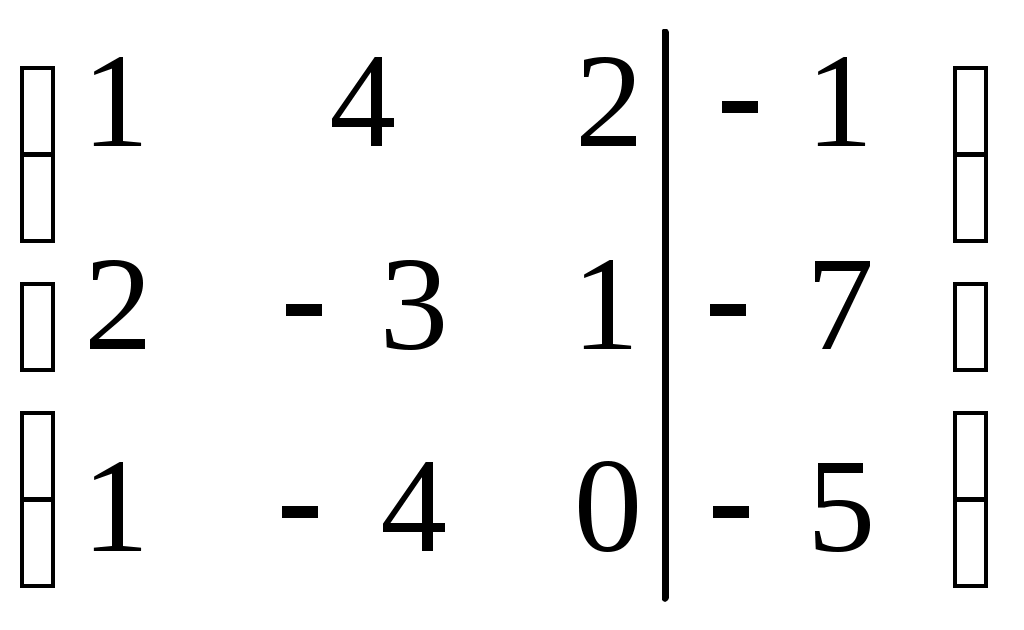 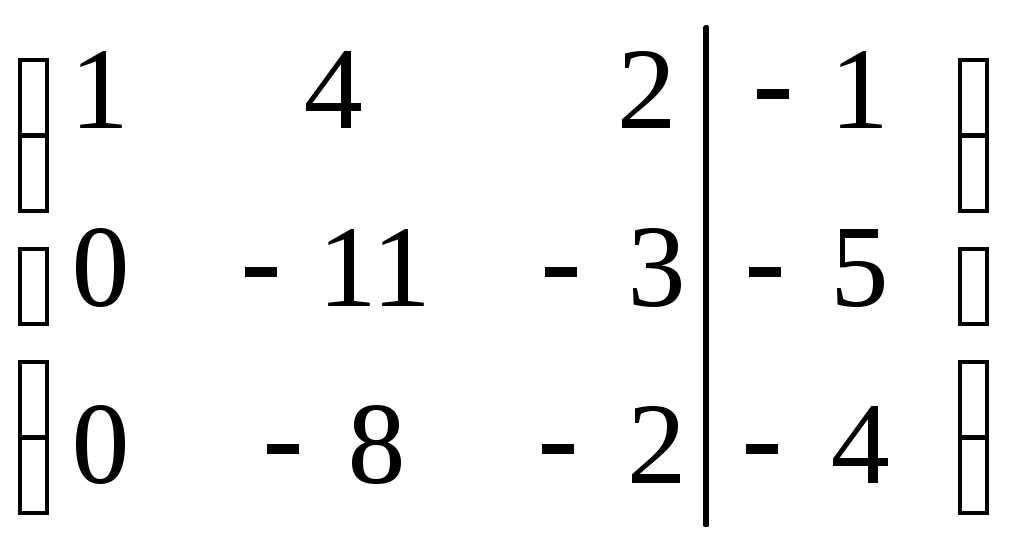 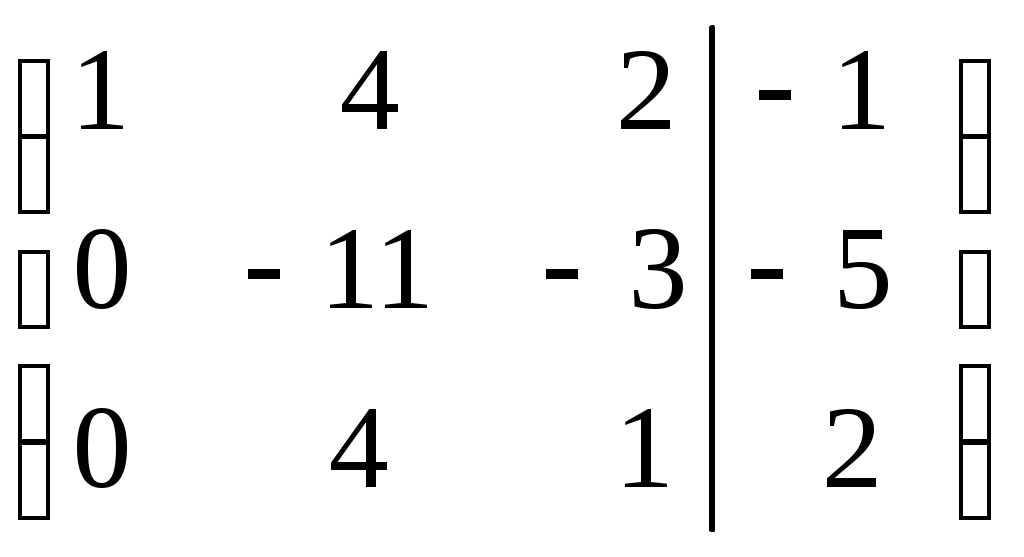 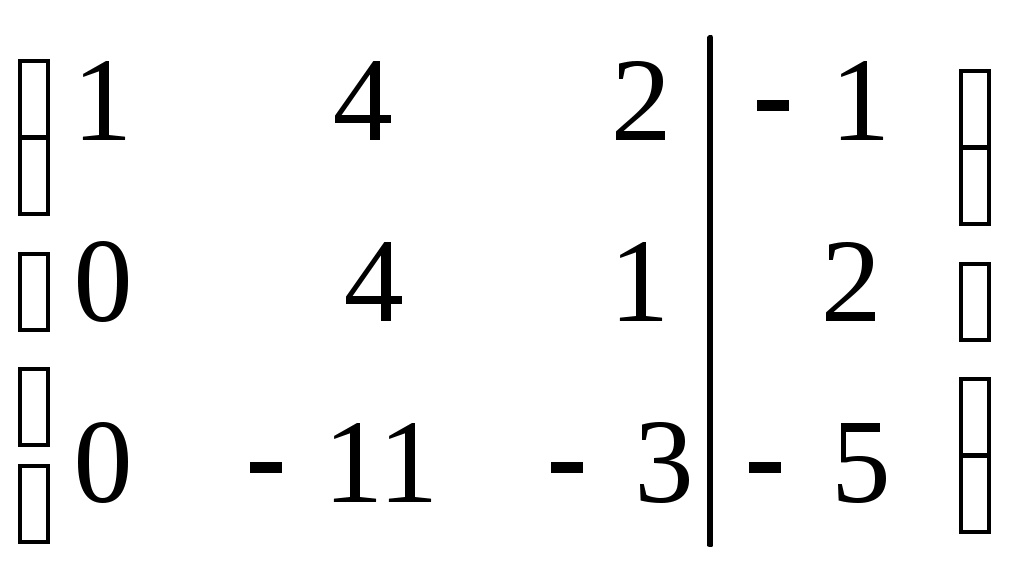 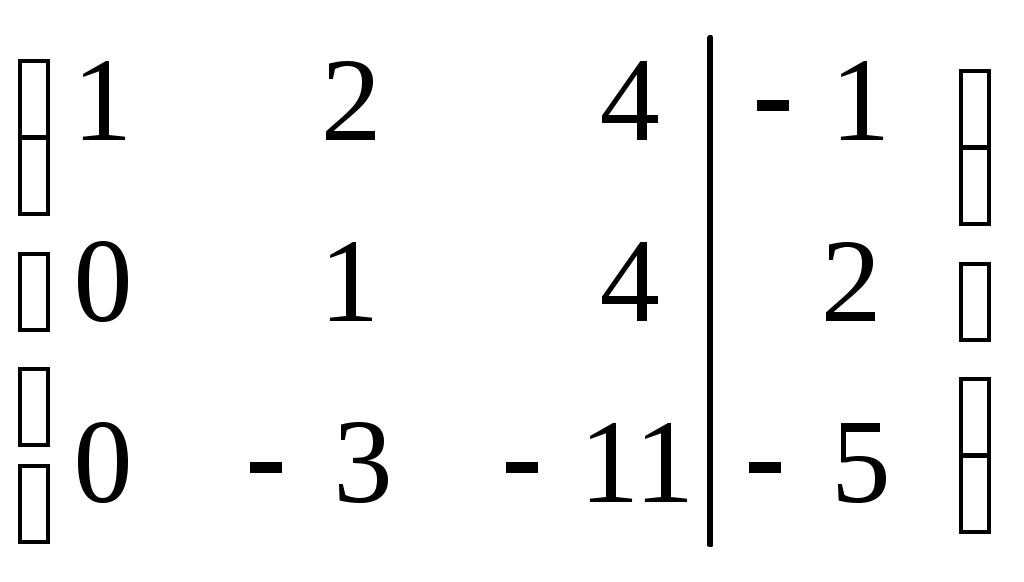 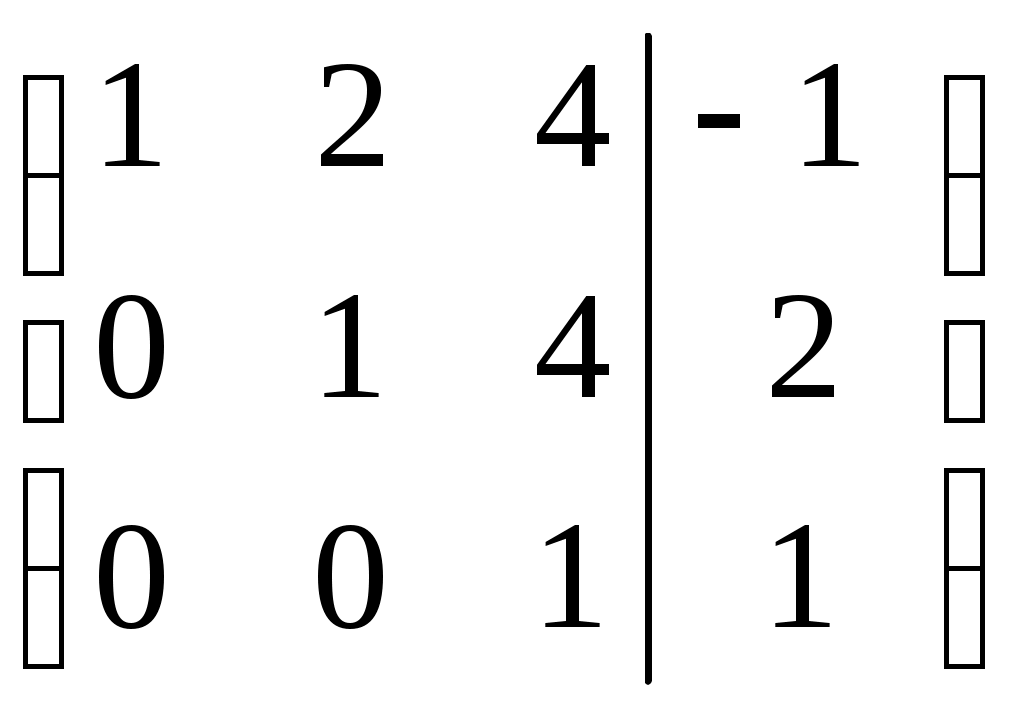 . .Расширенная матрица приведена к треугольному виду. Соответствующая ей система имеет вид: 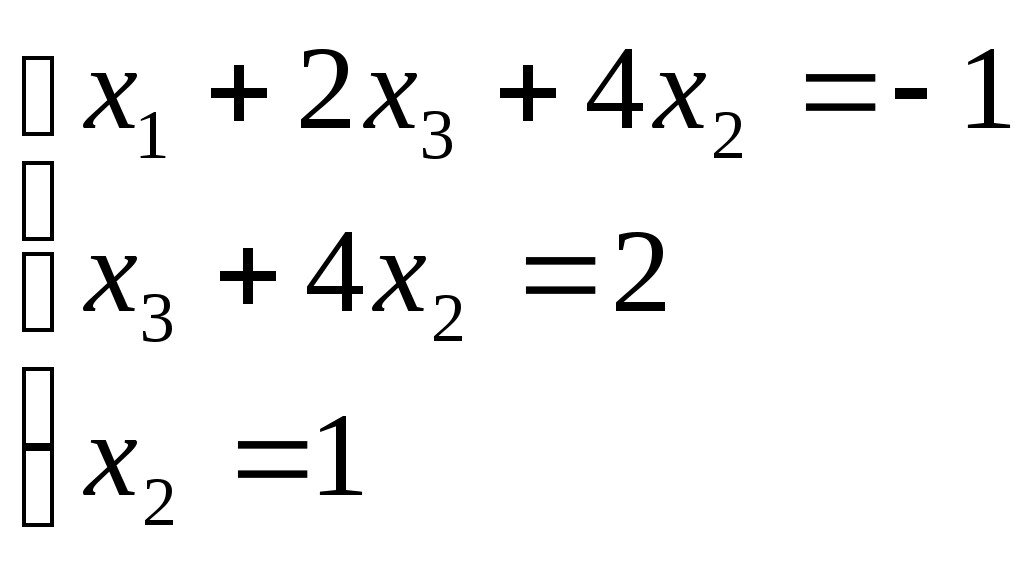 Из последнего уравнения Таким образом, 10. Решение систем п линейных уравнений с п переменными с помощью обратной матрицы (вывод формулы Х=А –1В). Для получения решения системы 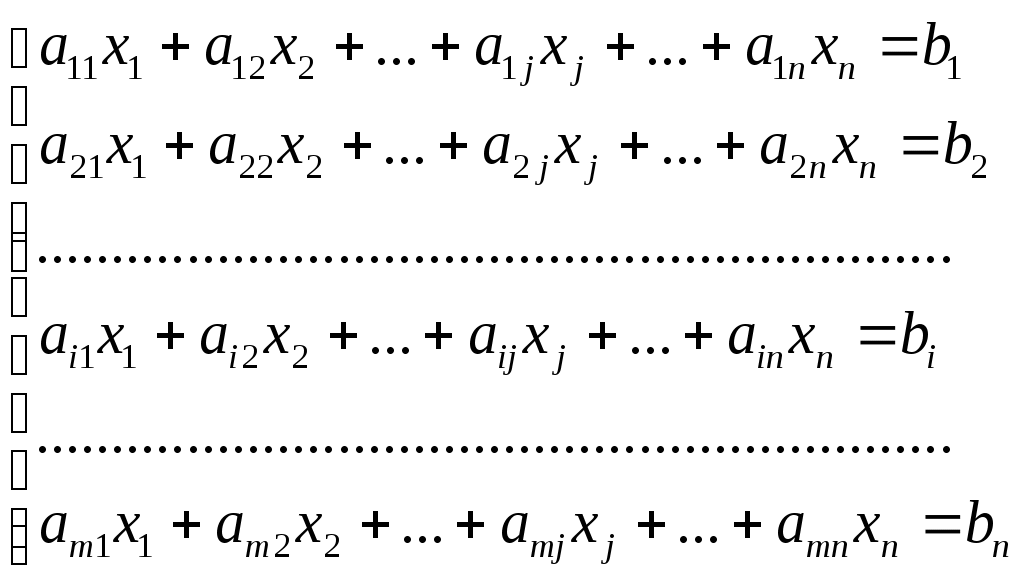 при при Метод обратной матрицы. Запишем систему в матричной форме: 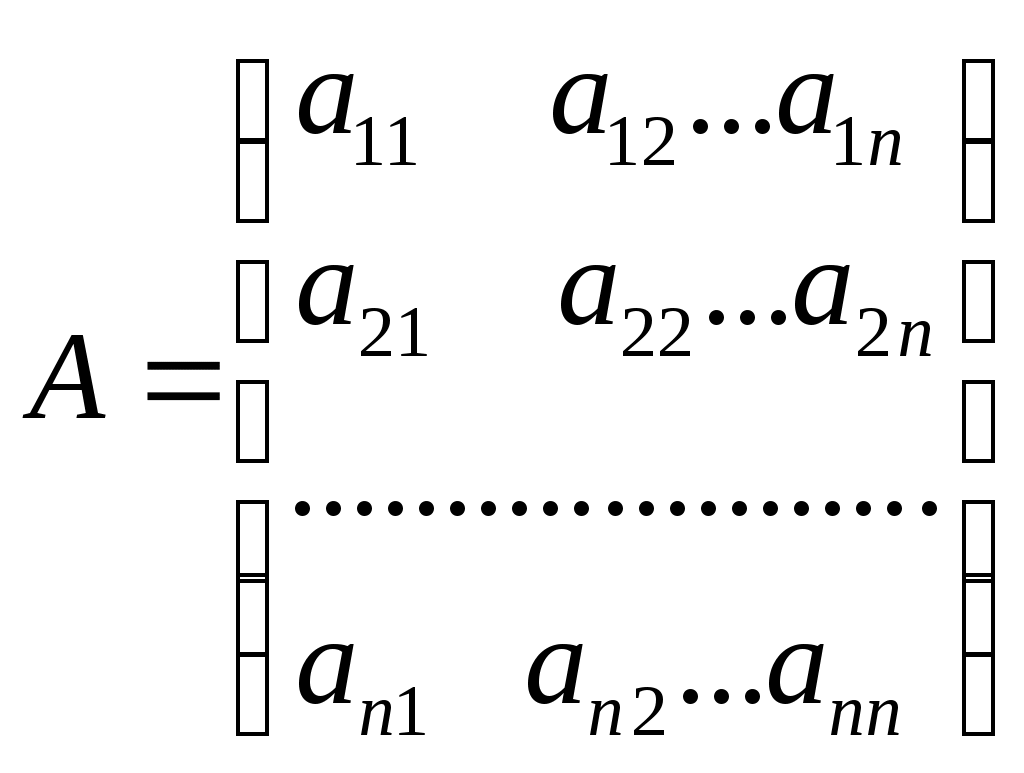 - матрица коэффициентов при переменных, - матрица коэффициентов при переменных,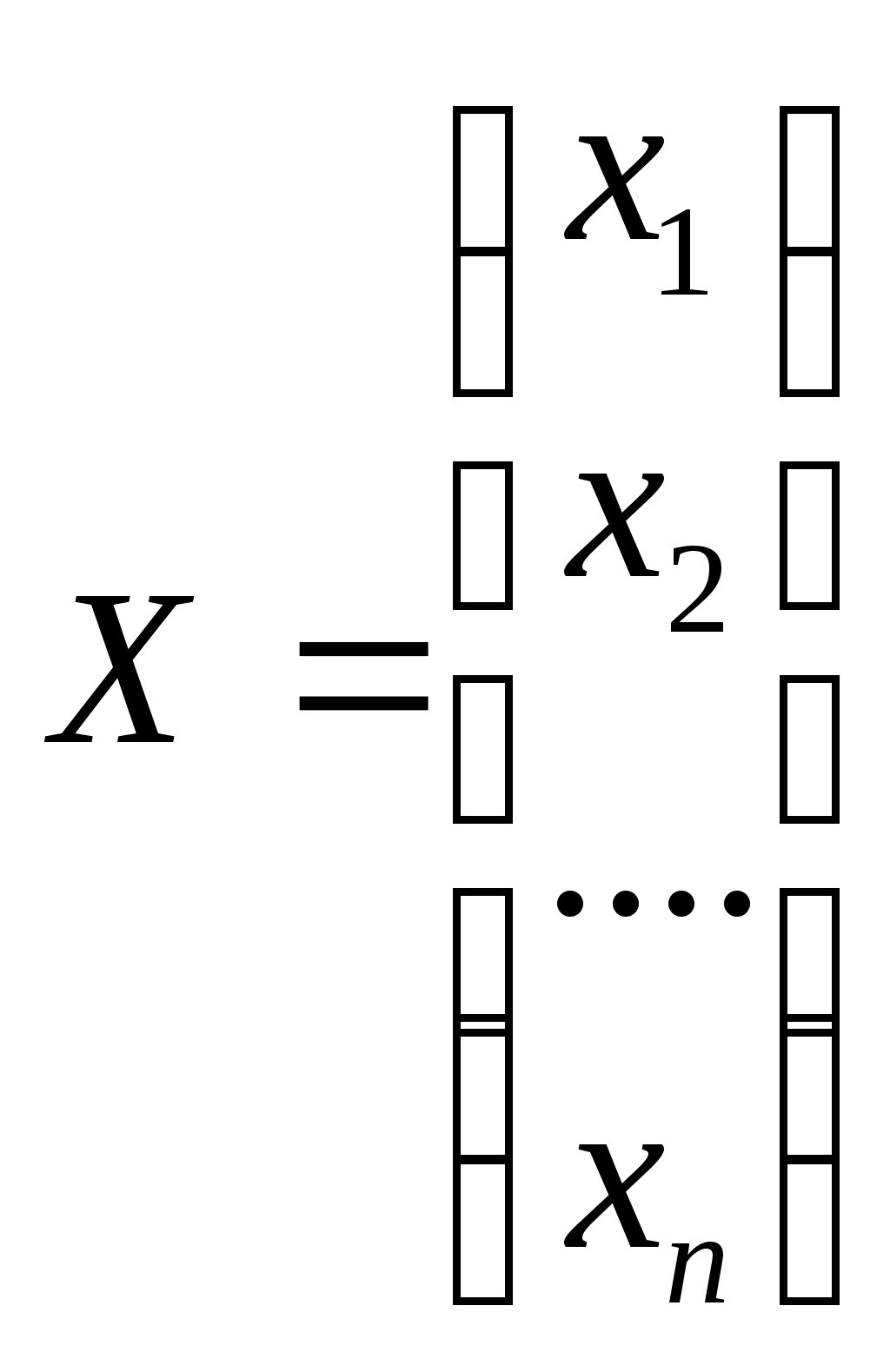 - матрица-столбец переменных; - матрица-столбец переменных; 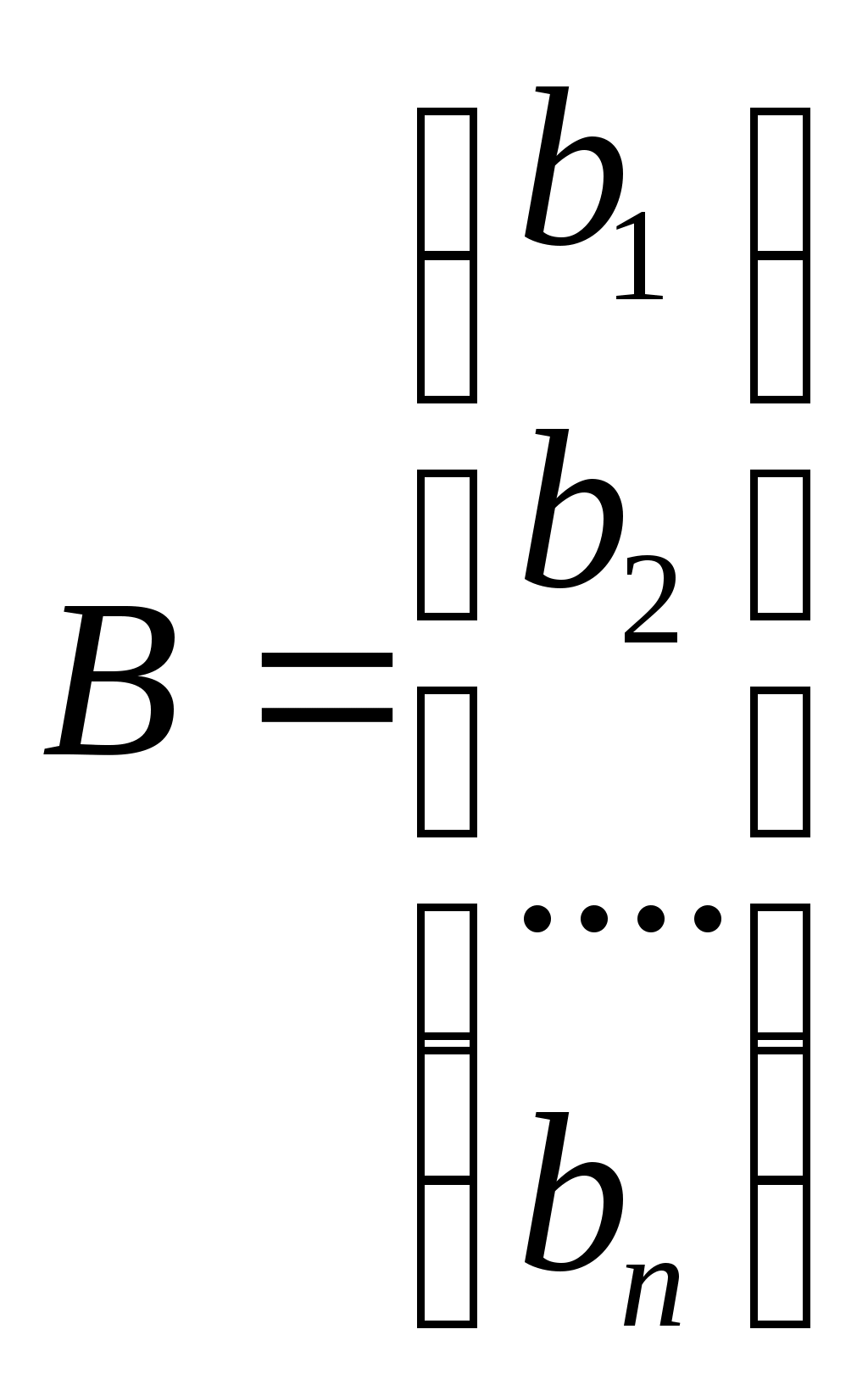 - матрица столбец свободных членов. - матрица столбец свободных членов.Умножим слева обе части равенства на матрицу Таким образом, решение системы в матричном виде Пример. Решить систему уравнений методом обратной матрицы. 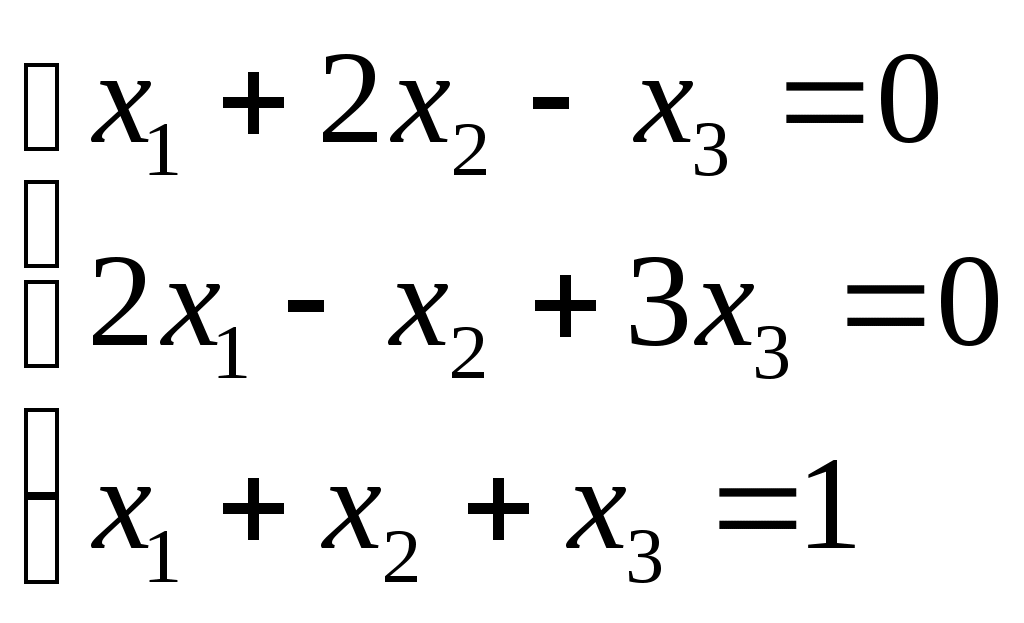 Р е ш е н и е: Обозначим 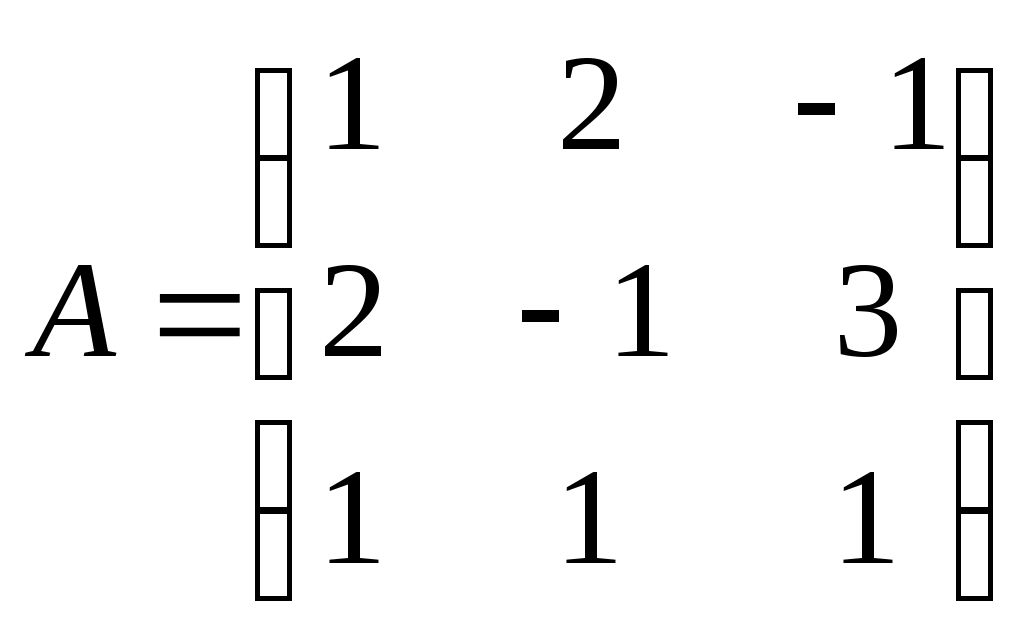 ; ; 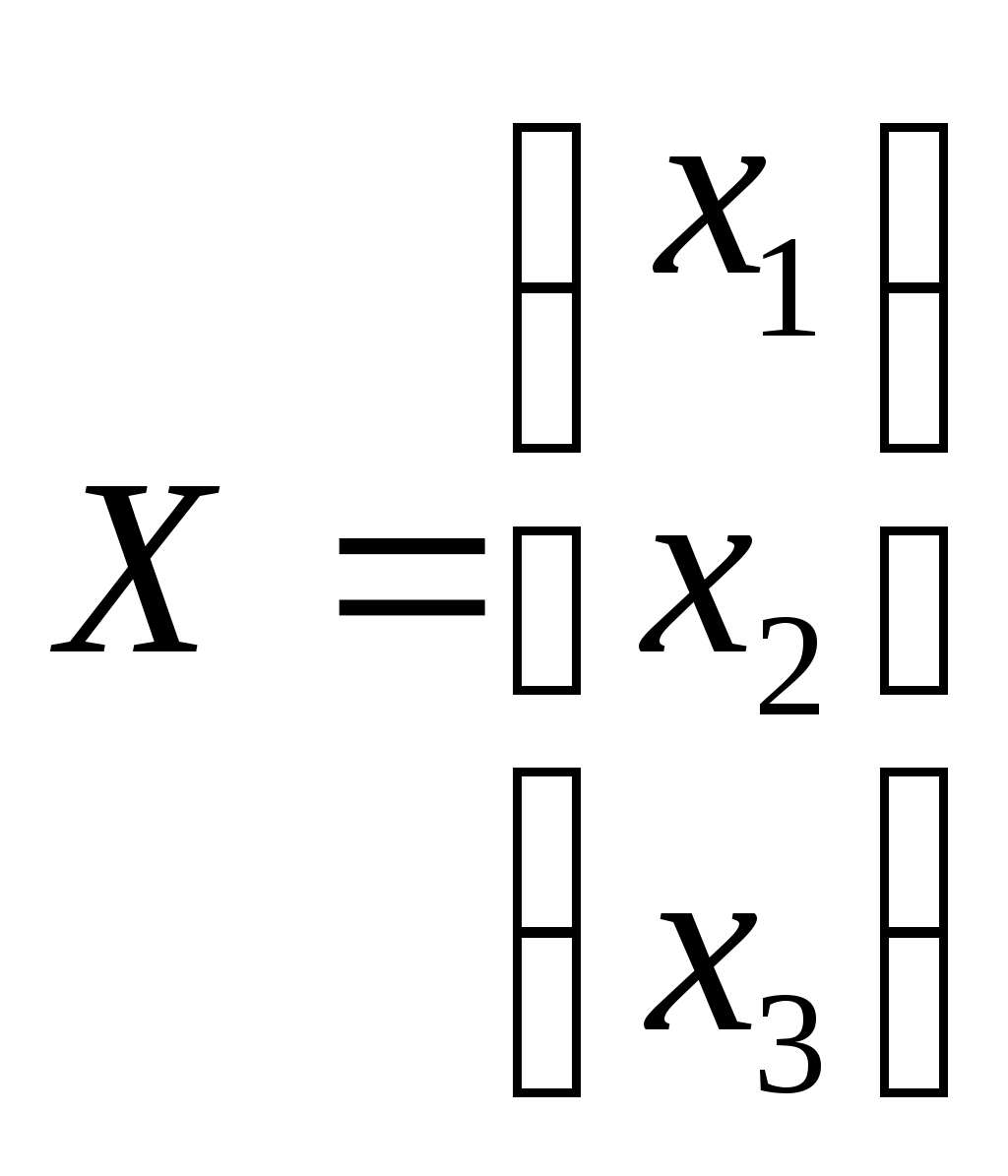 ; ; 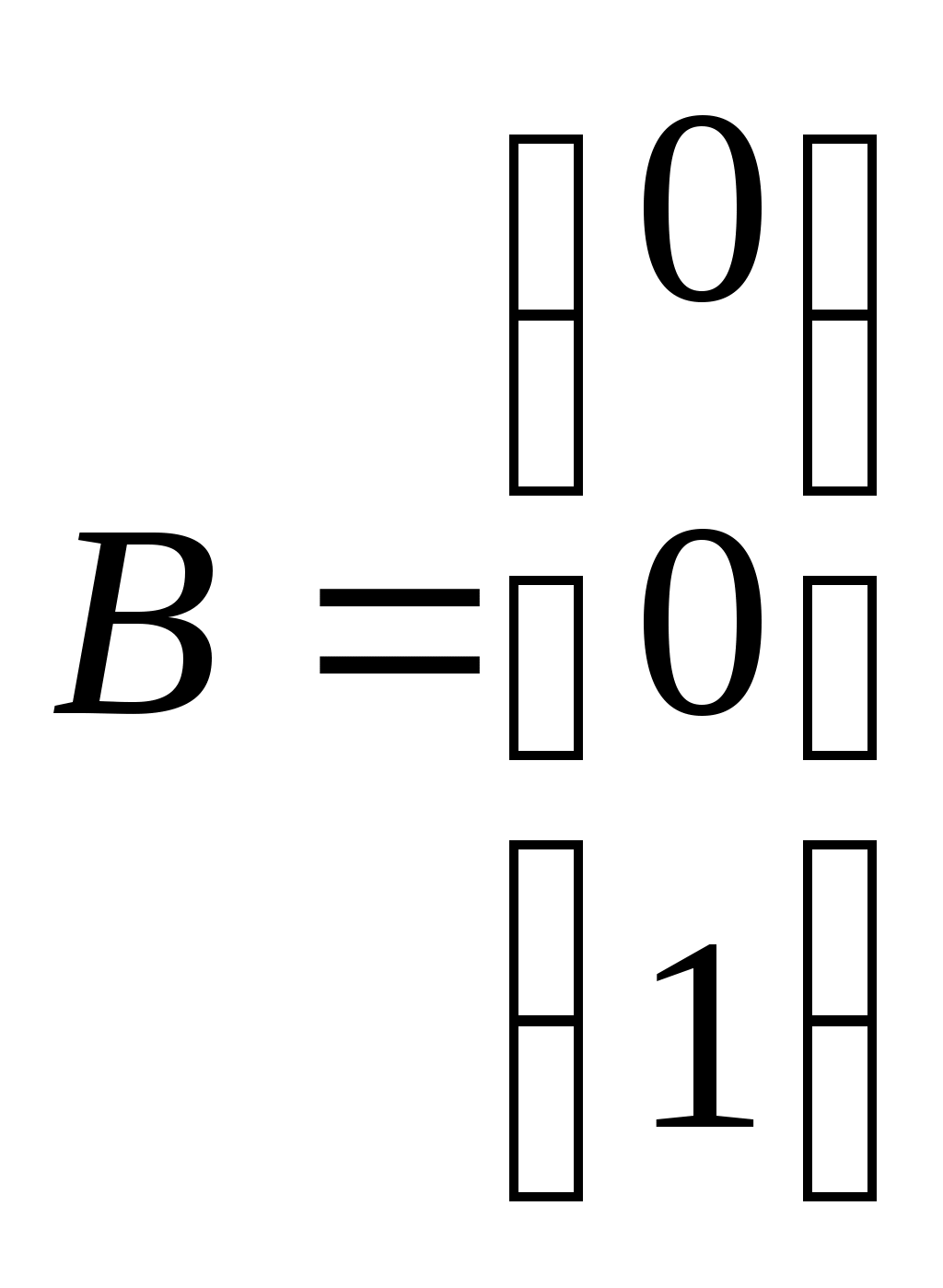 . .Тогда в матричной форме система имеет вид: 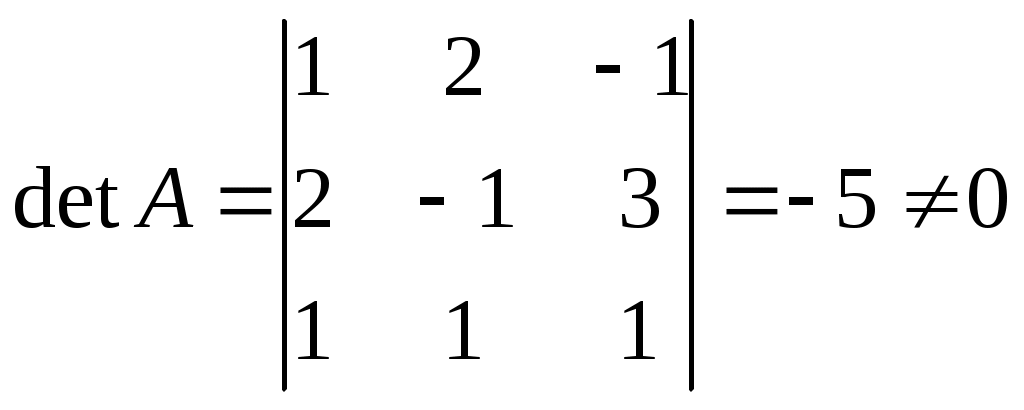 , т.е. обратная матрица , т.е. обратная матрица 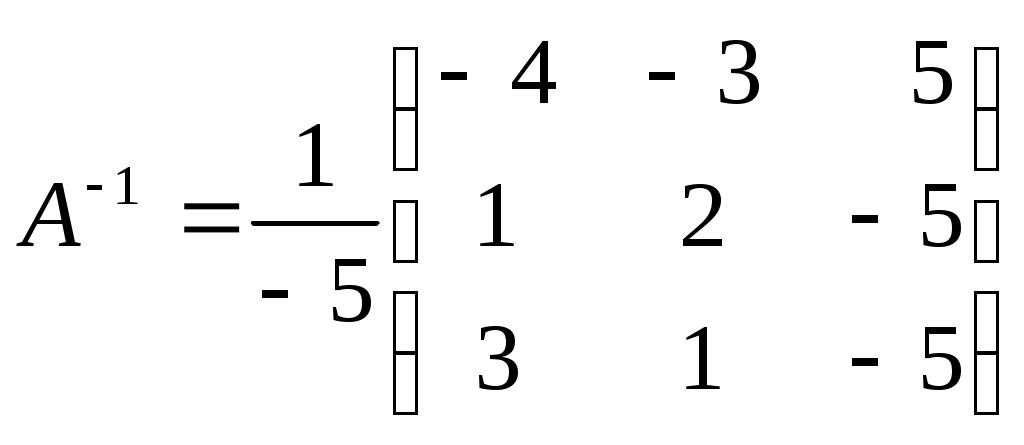 . . Определим 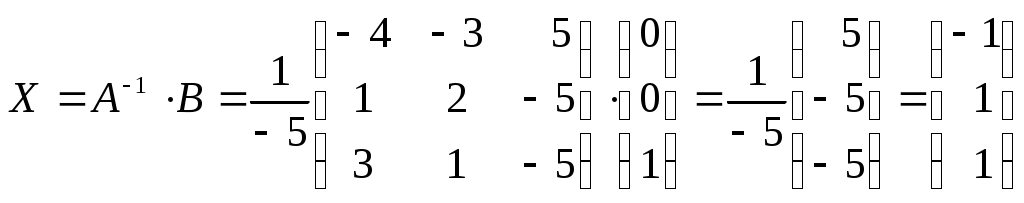 , ,Существенным недостатком решения систем 11. Теорема и формулы Крамера решения системы п линейных уравнений с п переменными (без вывода). Теорема Крамера. Пусть - определитель матрицы системы, а - определитель матрицы, получаемой из матрицы заменой -го столбца столбцом свободных членов. Тогда, если , то система имеет единственное решение, определяемое по формулам: В соответствии с обратной матрицей , где - матрица, присоединенная к матрице . Т.к. элементы матрицы есть алгебраические дополнения элементов матрицы , транспонированной к , то запишем равенство . Учитывая, что , получим после умножения матриц: , откуда следует, что для любого . На основании свойства 9 определителей , где - определитель матрицы, полученной из матрицы заменой -го столбца столбцом свободных членов. Следовательно Решение системы Рассмотрим систему Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы: Для совместных систем линейных уравнений верны следующие теоремы: Теорема 1. Если ранг матрицы совместной системы равен числу переменных, т.е. Теорема 2. Если ранг матрицы совместной системы меньше числа переменных, т.е. Определение. Базисным минором матрицы называется любой ненулевой минор, порядок которого равен рангу матрицы. Определение. Те Решить систему уравнений в случае Пример. Решить систему методом Гаусса: 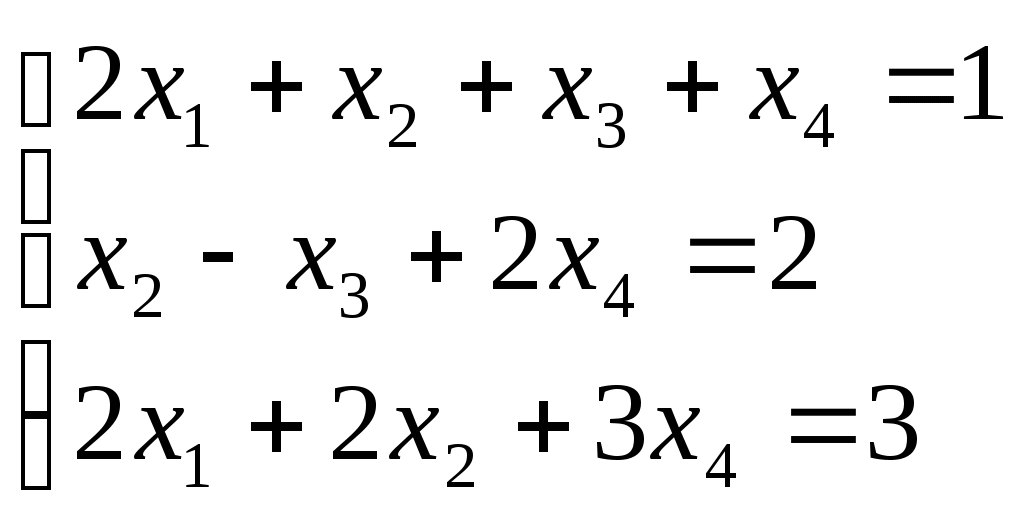 Р е ш е н и е. Выпишем и преобразуем расширенную матрицу системы. Сначала прибавим к элементам третьей строки элементы первой строки, умноженные на –1. А затем элементы второй строки умножим на –1 и прибавим к элементам третьей строки: 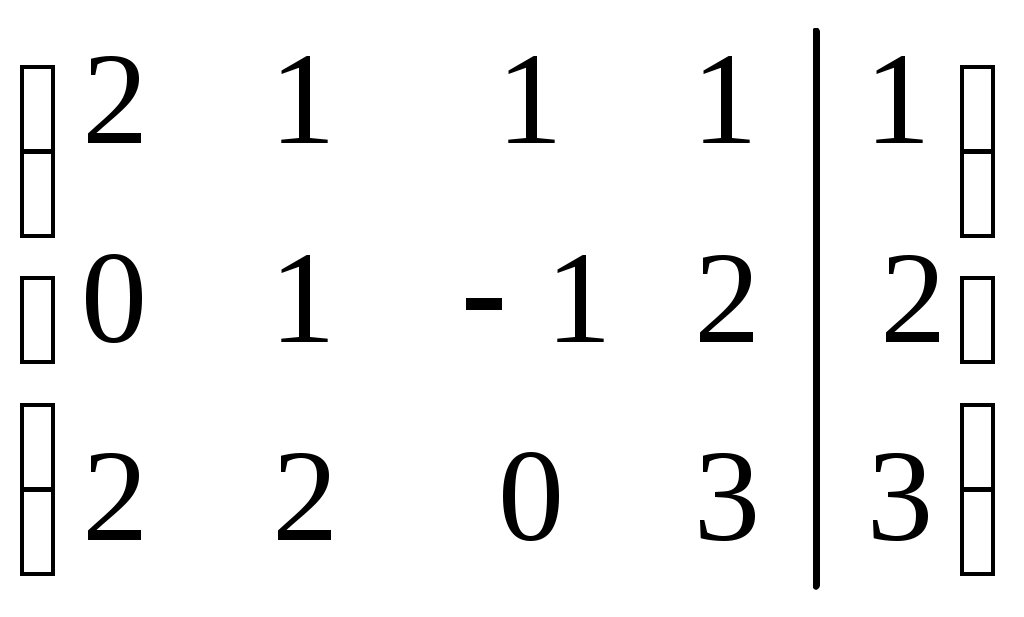 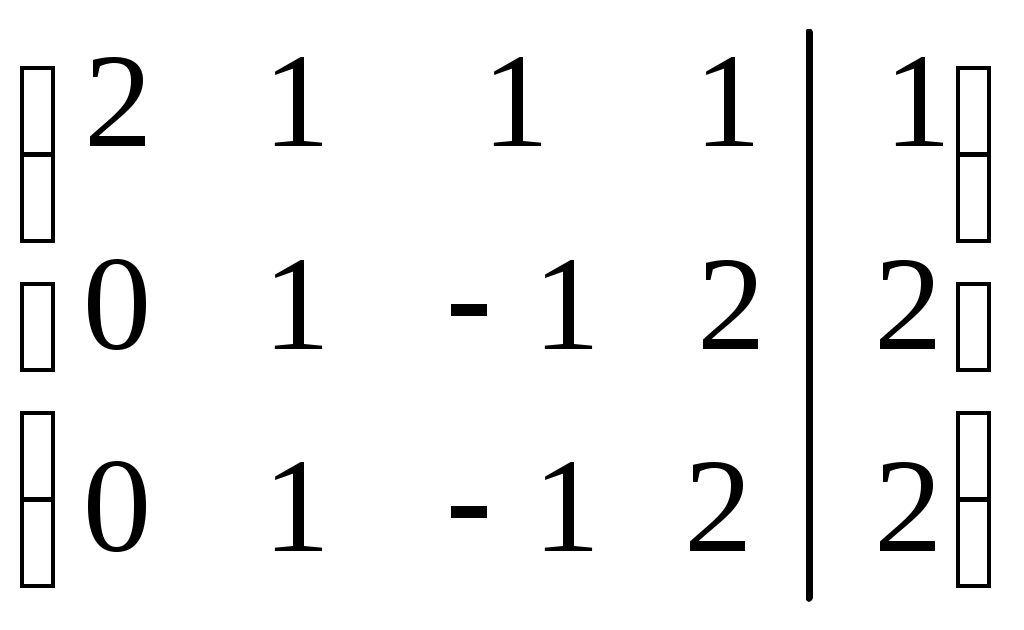 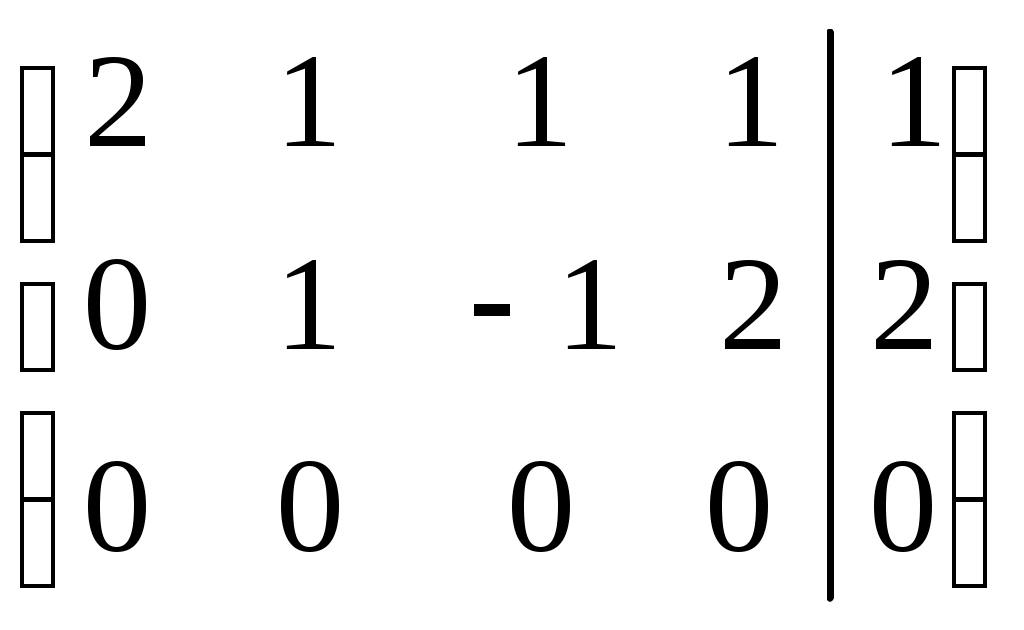 . .Расширенная матрица приведена к ступенчатому виду. Выразим базисные переменные через свободные. Из второй строки полученной матрицы выразим переменную Из первой строки выразим Общее решение системы уравнений: 12. Понятие функции, способы задания функций. Область определения. Четные и нечетные, ограниченные, монотонные функции. Примеры. Понятие функции одной переменной Постоянной величиной называется величина, сохраняющая одно и то же значение. Например, отношение длины окружности к ее диаметру есть постоянная величина, равная числу . Если величина сохраняет постоянное значение лишь в условиях данного процесса, она называется параметром. Переменной называется величина, которая может принимать различные числовые значения. Например, при равномерном движении: Определение. Если каждому элементу множества ставится в соответствие вполне определенный элемент множества , то тогда говорят, что на множестве задана функция . При этом называется независимой переменной (или аргументом), - зависимой переменной, а буква обозначает закон соответствия. Множество называется областью определения (или существования) функции, а множество - областью значений функции. Если множество специально не оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменной , т.е. множество таких значений , при которых функция вообще имеет смысл. Способы задания функций: а) Аналитический способ, если функция задана формулой вида . Этот способ наиболее часто встречается на практике. Например, функция 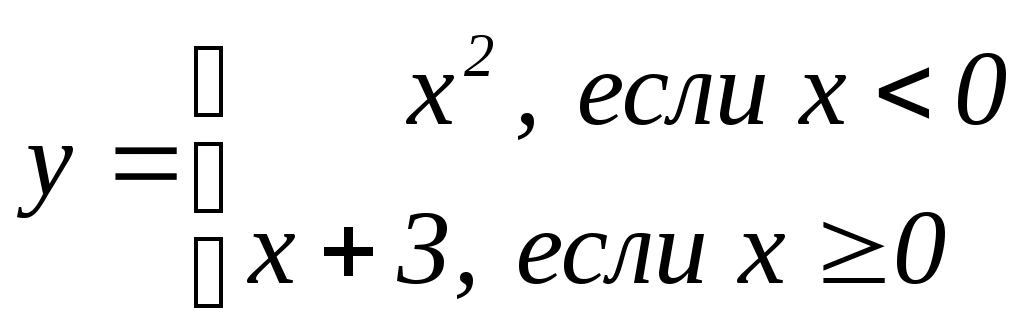 имеет два аналитических выражения: имеет два аналитических выражения: б) Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента и соответствующие значения функции , например, таблица логарифмов, гармонические функции и т.д. в) Графический способ состоит в изображении графика функции - множества точек г) Словесный способ, если функция описывается правилом ее составления, например, функция Дирихле: , если - иррационально. Основные свойства функций 1) Четность и нечетность. Функция называется четной, если для любых значений из области определения и нечетной, если . В противном случае функция называется функцией общего вида. Пример.
График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат. 2) Монотонность. Функция называется возрастающей (убывающей) на промежутке , если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции. Функции возрастающие и убывающие называются монотонными функциями. Пример.
3) Ограниченность. Функция называется ограниченной на промежутке , если существует такое положительное число - ограничена на всей числовой оси, т.к. для любого . 4) Периодичность. Функция Пример.
13. Понятие элементарной функции. Основные элементарные функции и их графики (постоянная, степенная, показательная, логарифмическая). Элементарная функция Из основных функции новые функции могут быть получены двумя способами при помощи: а) алгебраических действий; б) операции образования сложной функции. Определение. Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными. Пример. 1) 2) - неэлементарная функция. Основные элементарные функции Постоянная функция: y = b.
Степенная функция. а) Степенная функция с натуральным показателем (n – натуральное число: ). (непериодическая)
б) Степенная функция с целым отрицательным показателем (n – натуральное число: ). (непериодическая)
в) Степенная функция с положительным показателем меньше единицы (n – натуральное число больше единицы: ; ). (непериодическая).
Показательная функция
Логарифмическая функция
14. Уравнение линии на плоскости. Точка пересечения двух линий. Основные виды уравнений прямой на плоскости (одно из них вывести). Уравнение линии на плоскости Определение. Уравнением линии (кривой) на плоскости называется уравнение, которому удовлетворяют координаты и каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии. Е  сли точка передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты называются текущими координатами. сли точка передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты называются текущими координатами.Любую линию в принципе можно выразить соответствующим уравнением. Однако не всякое уравнение на определяет на плоскости некоторую линию. Например: определяет только одну точку (0;0); не определяет никакого множества точек, т.к. левая часть уравнения не может равняться нулю. Чтобы убедится, лежит ли точка на данной линии , надо проверить, удовлетворяют ли координаты этой точки уравнению . Уравнения линии могут быть самыми различными, однако надо отметить, что не каждое уравнение имеет геометрический образ в виде линии. |