Ответы на экзамен по Линейной алгебре. ответы на экзамен по Линейной Алгебре. 1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами умножение на число, сложение, умножение матриц

• Название: 1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами умножение на число, сложение, умножение матриц
• Анкор: Ответы на экзамен по Линейной алгебре
• Дата: 22.01.2023
• Размер: 2.37 Mb.
• Имя файла: ответы на экзамен по Линейной Алгебре.doc
• Тип: Решение; #898154
• страница: 4 из 10

Ранг матрицы. Линейная независимость строк матрицы

Для решения и исследования ряда математических и прикладных задач важное значение имеет понятие ранга матрицы.

В матрице размером вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы -го порядка, где . Определители таких подматриц называются минорами -го порядка матрицы .

Например, из матриц можно получить подматрицы 1, 2 и 3-го порядка.

Определение. Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы. Обозначение: или .

Из определения следует:

1) Ранг матрицы не превосходит меньшего из ее размеров, т.е. .

2) тогда и только тогда, когда все элементы матрицы равны нулю, т.е. .

3) Для квадратной матрицы n-го порядка тогда и только тогда, когда матрица - невырожденная.

Поскольку непосредственный перебор всех возможных миноров матрицы , начиная с наибольшего размера, затруднителен (трудоемок), то пользуются элементарными преобразованиями матрицы, сохраняющими ранг матрицы.

Элементарные преобразования матрицы:

1. 
   Отбрасывание нулевой строки (столбца).
   
2. 
   Умножение всех элементов строки (столбца) на число .
   
3. 
   Изменение порядка строк (столбцов) матрицы.
   
4. 
   Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
   
5. 
   Транспонирование матрицы.
   

Определение. Матрица , полученная из матрицы при помощи элементарных преобразований, называется эквивалентной и обозначается А В.

Теорема. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ее ранга не представляет труда.

Матрица 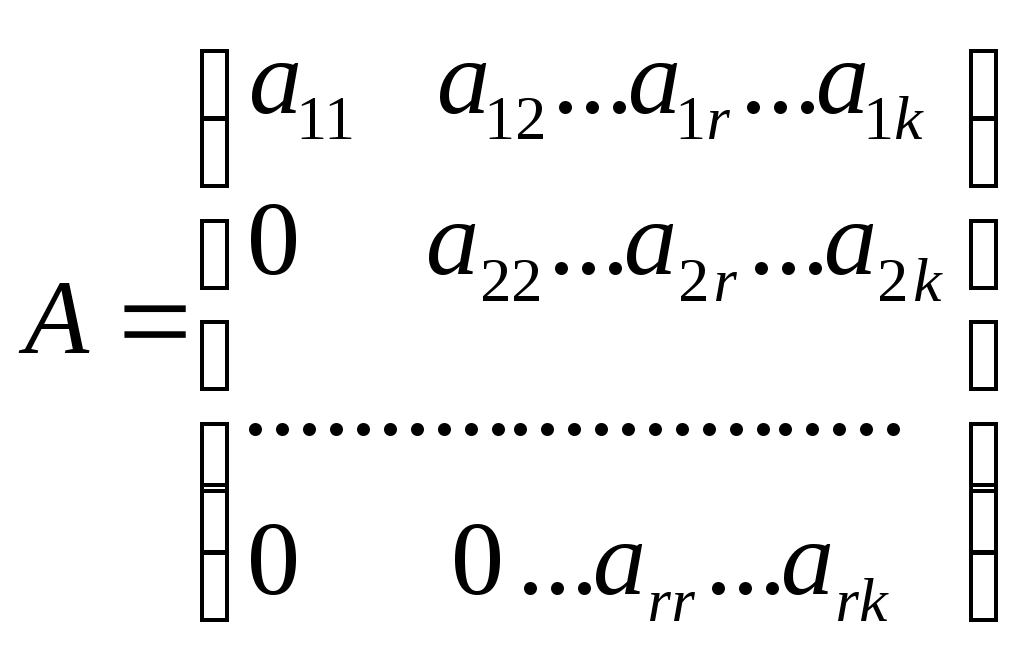называется ступенчатой если она имеет вид:

, где , , .

Очевидно, что ранг ступенчатой матрицы равен числу ненулевых строк 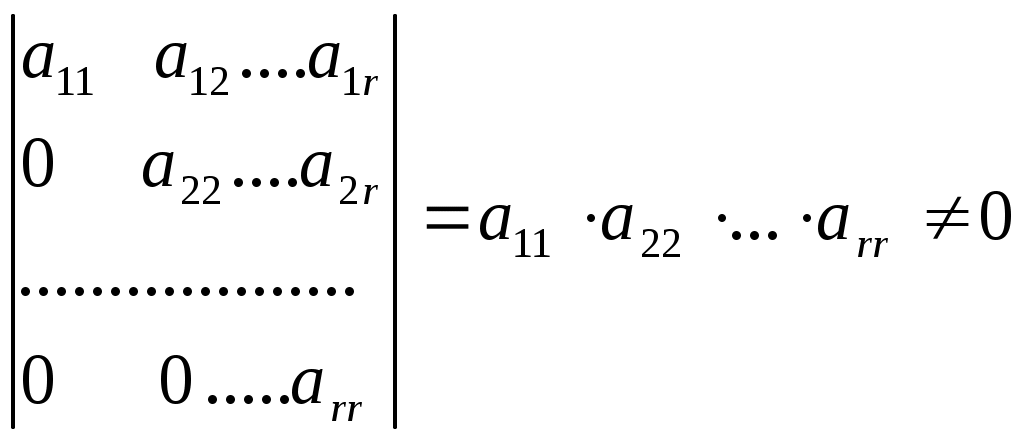, т.к. имеется минор -го порядка, не равный нулю:

.

Пример. Определить ранг матрицы с помощью элементарных преобразований.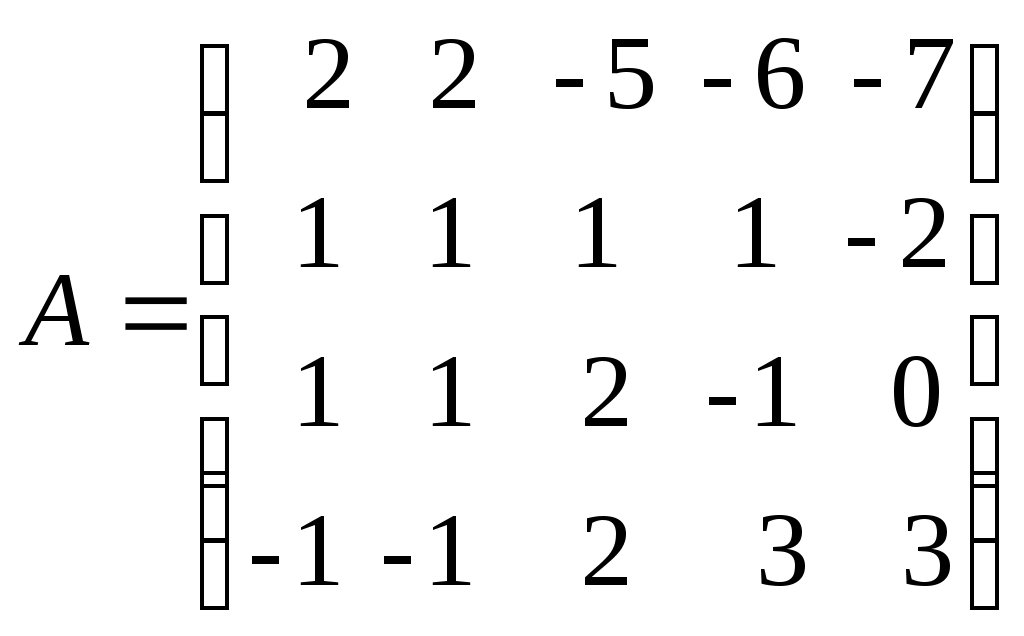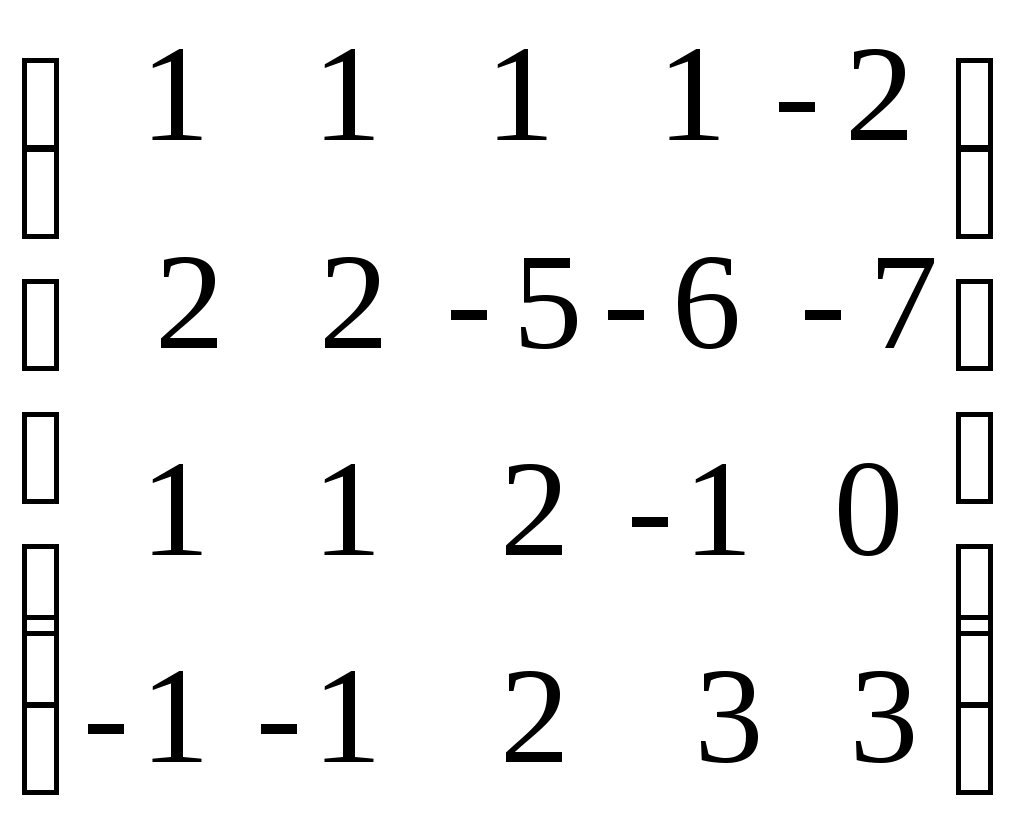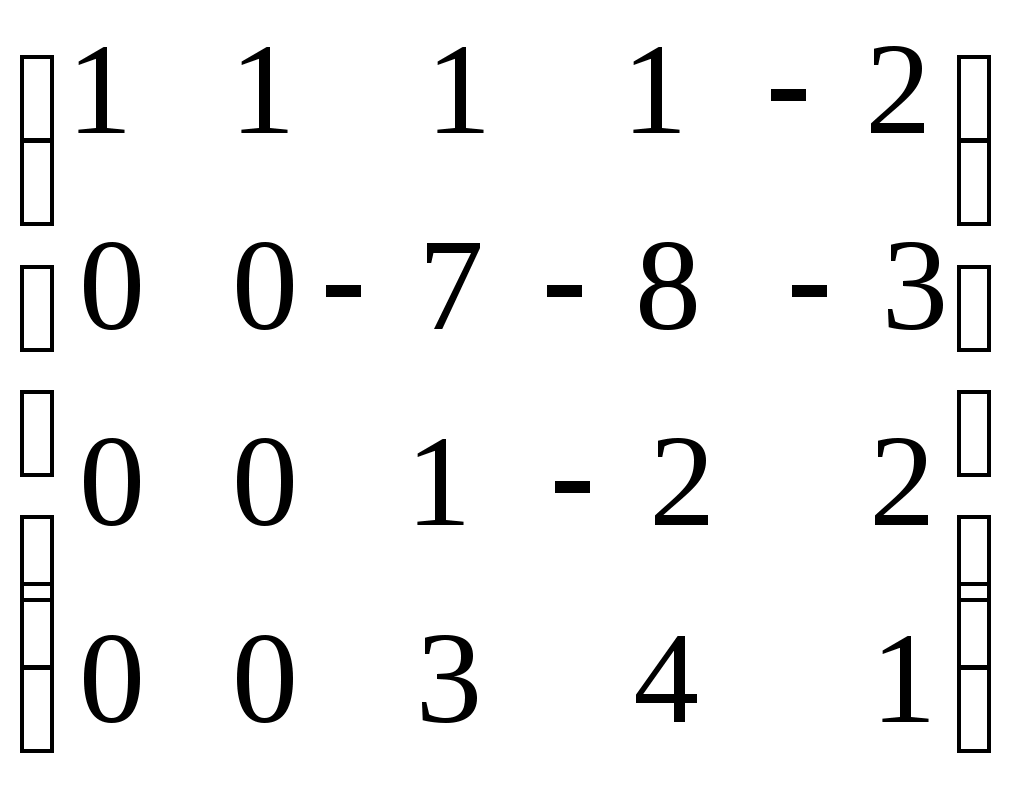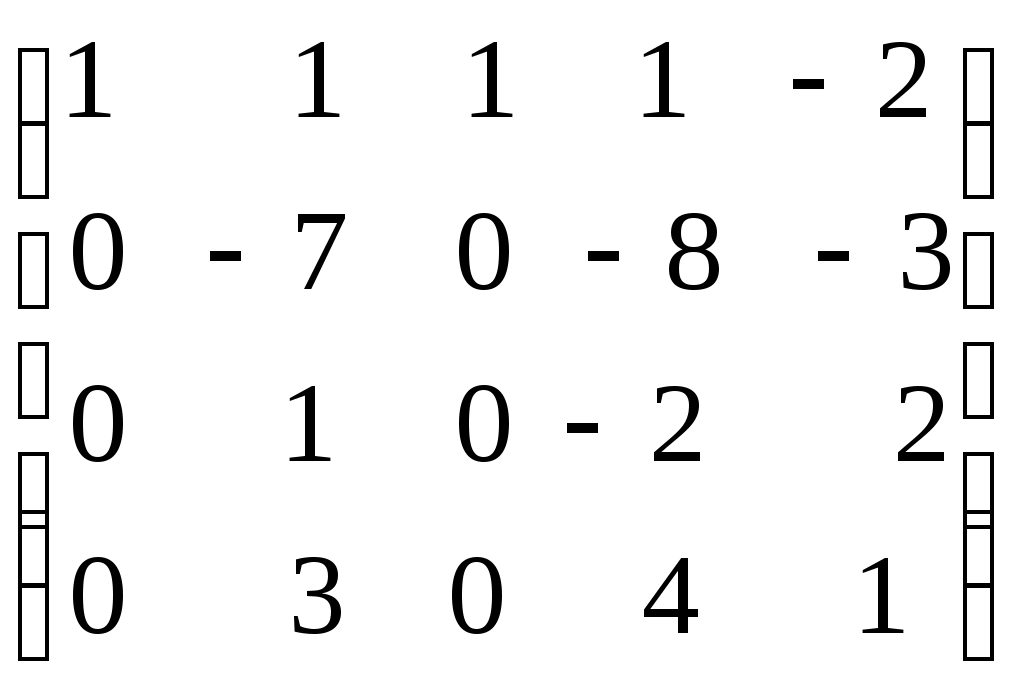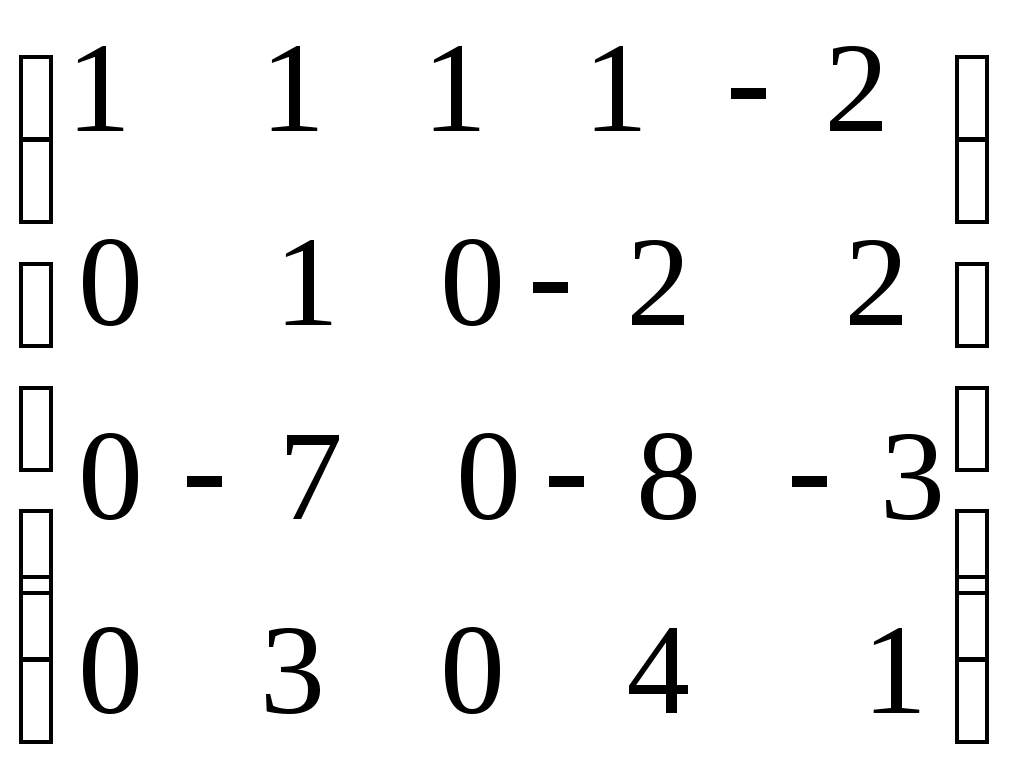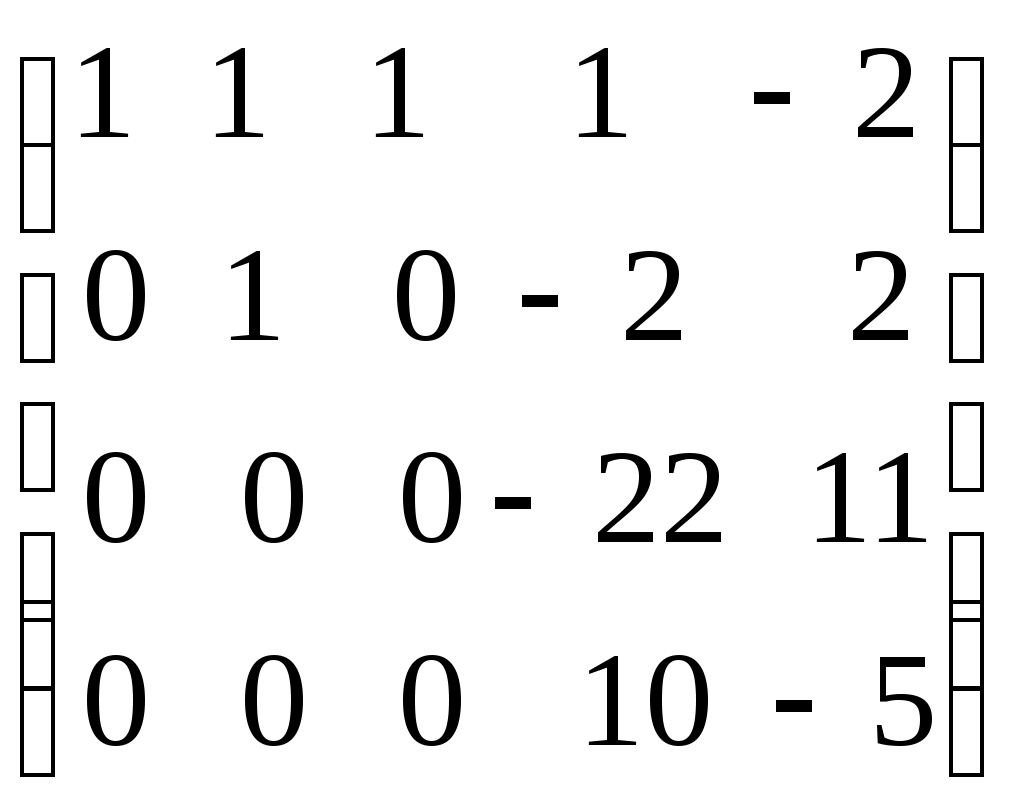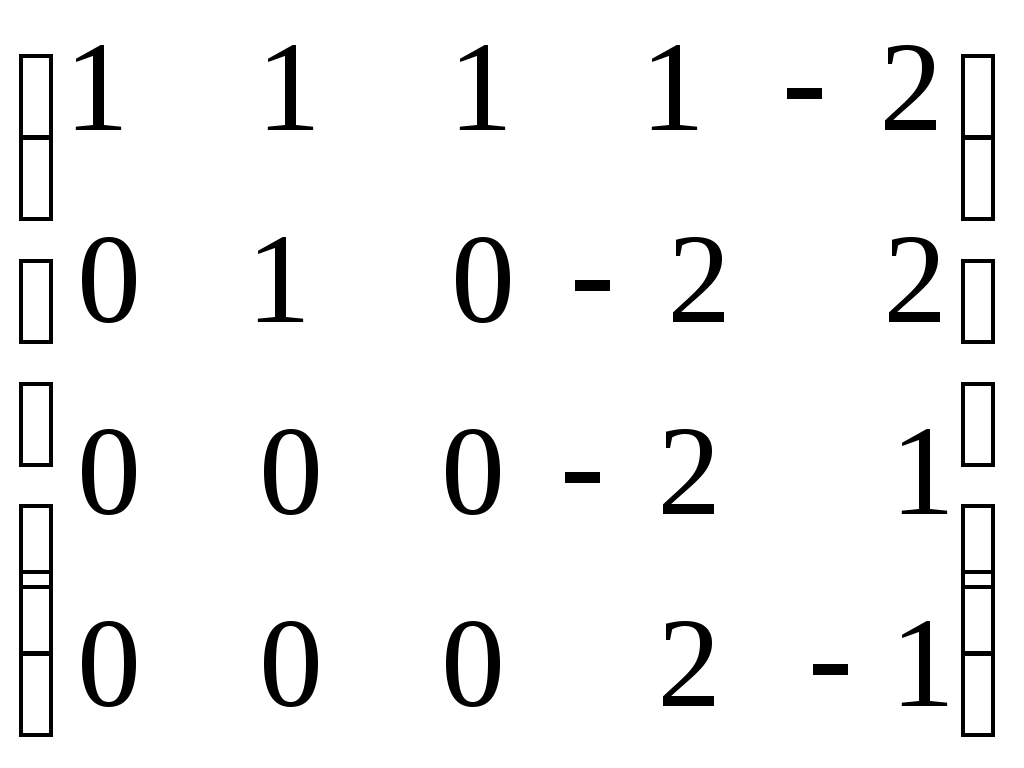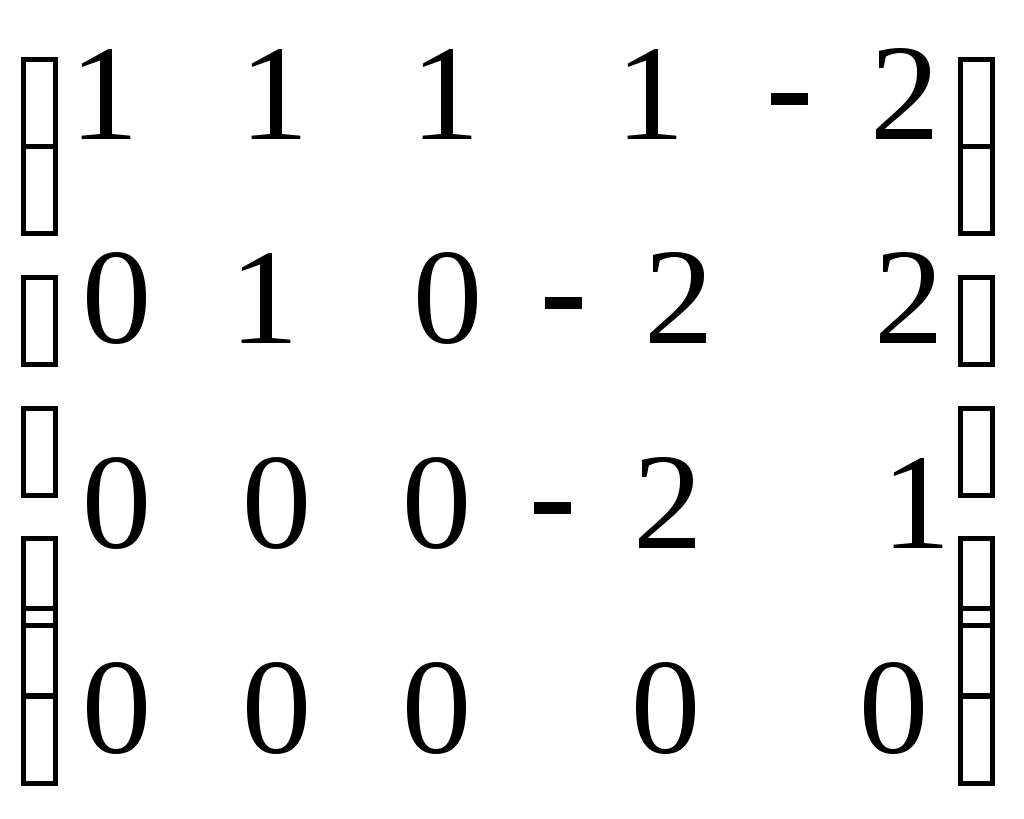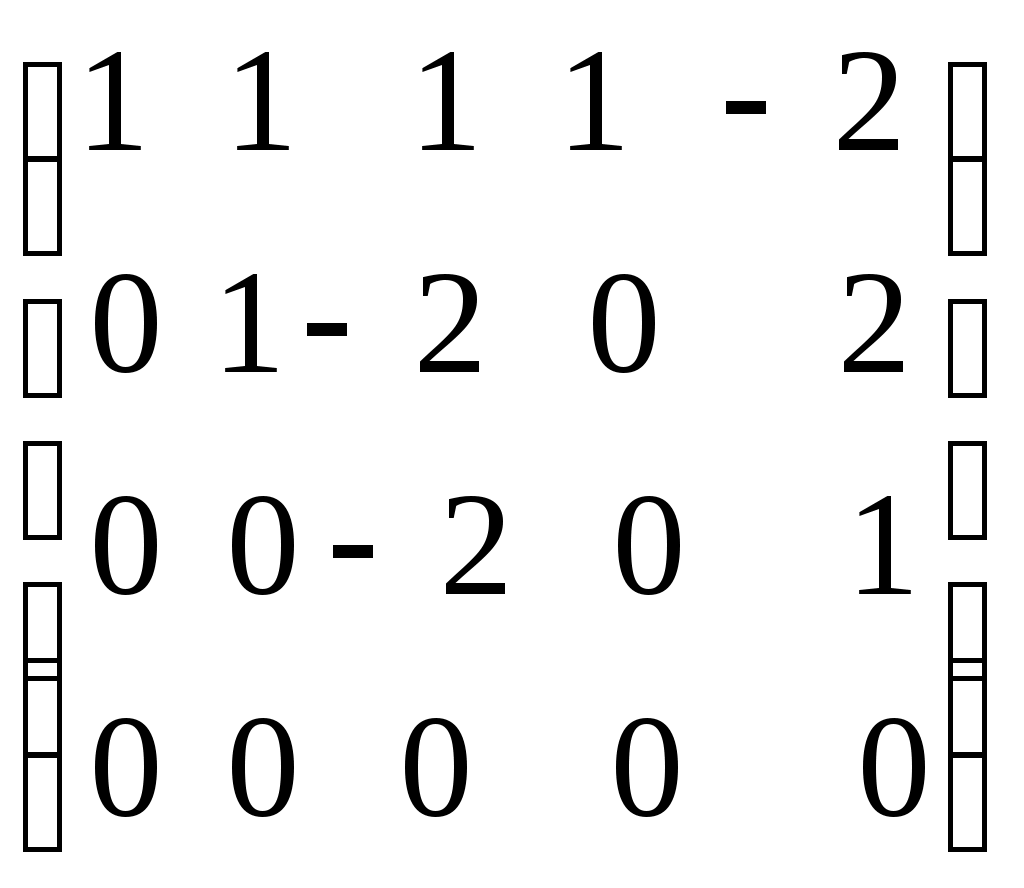

.

Ранг матрицы равен количеству ненулевых строк, т.е. .

5. Линейная независимость столбцов (строк) матрицы. Теорема о ранге матрицы.