|
|
Ответы на экзамен по Линейной алгебре. ответы на экзамен по Линейной Алгебре. 1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами умножение на число, сложение, умножение матриц
Определение. Число  называется пределом числовой последовательности называется пределом числовой последовательности 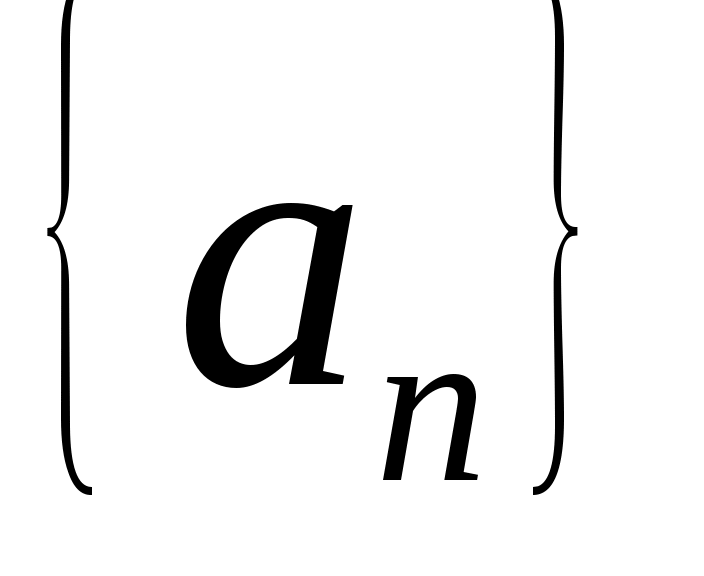 , если для любого, даже сколь угодно малого положительного числа , если для любого, даже сколь угодно малого положительного числа 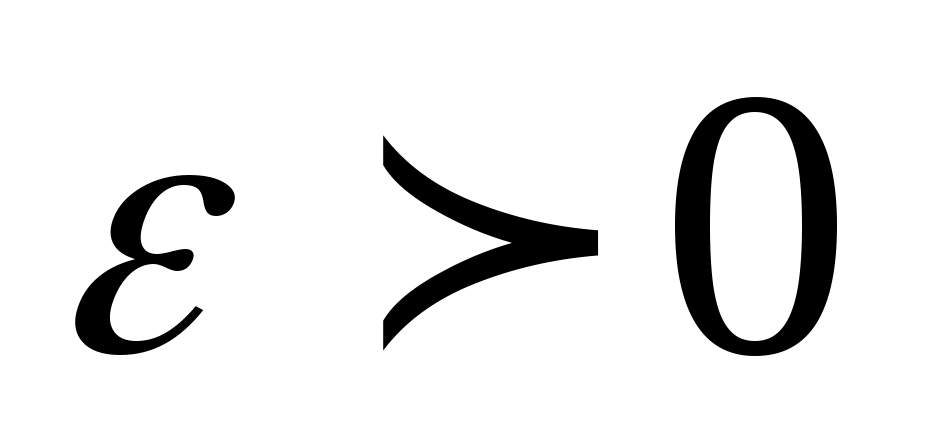 , найдется такой , найдется такой  (зависящий от (зависящий от 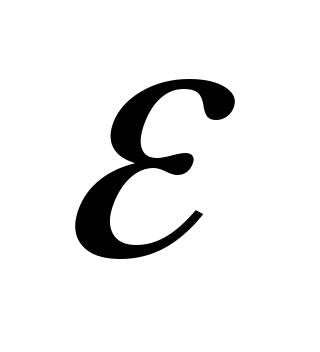 ), что для всех членов последовательности с номерами ), что для всех членов последовательности с номерами 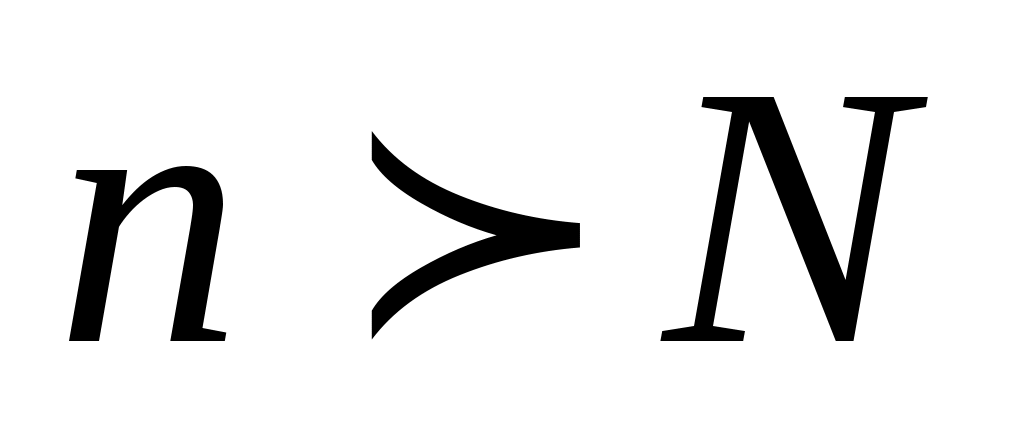 верно неравенство: верно неравенство:
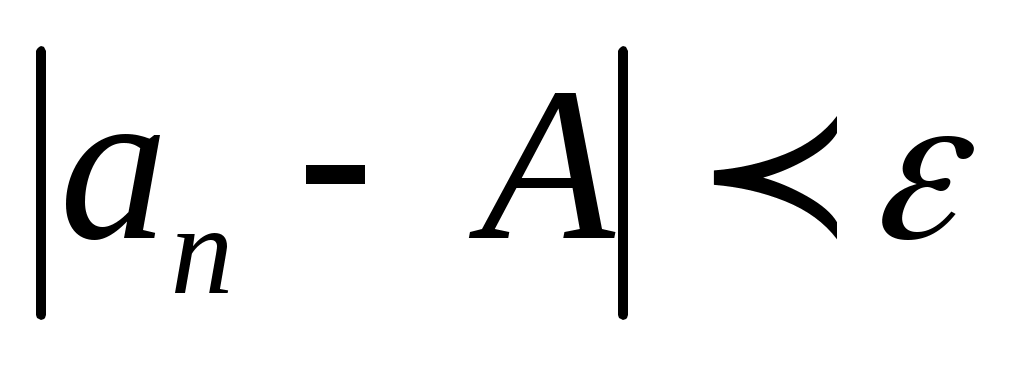 . .
Обозначают: 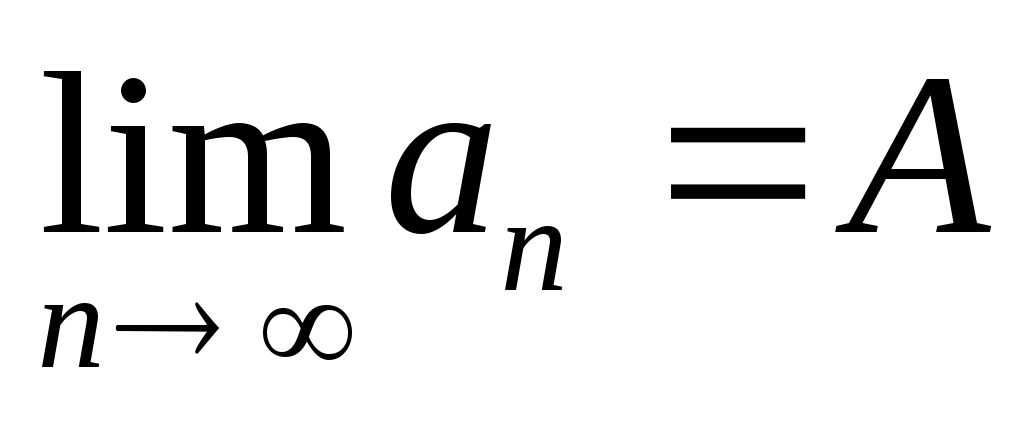 . Или . Или  при при  . .
Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.
Предел функции в бесконечности и в точке
Предел функции в бесконечности: С понятием предела числовой последовательности 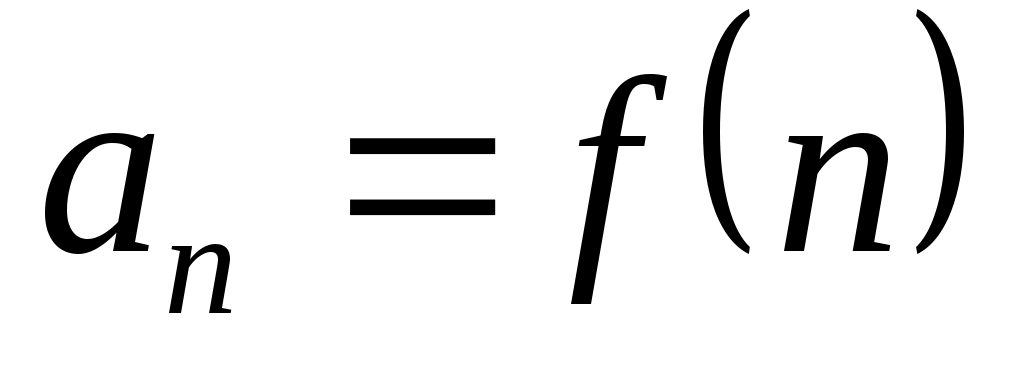 тесно связано понятие предела функции тесно связано понятие предела функции 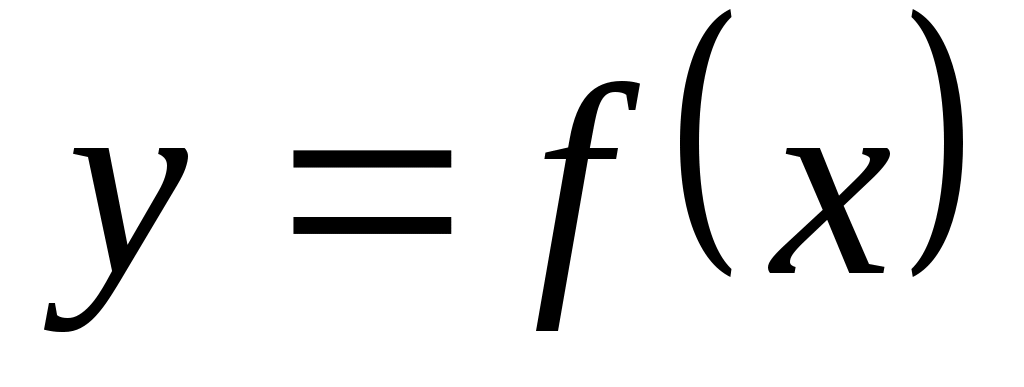 в бесконечности. Если в первом случае переменная в бесконечности. Если в первом случае переменная 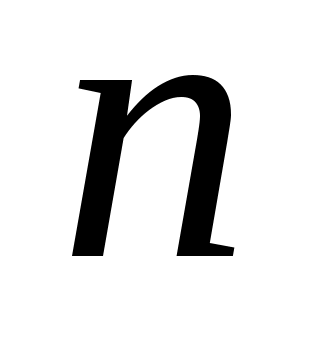 возрастая, принимает лишь целые значения, то во втором случае переменная возрастая, принимает лишь целые значения, то во втором случае переменная 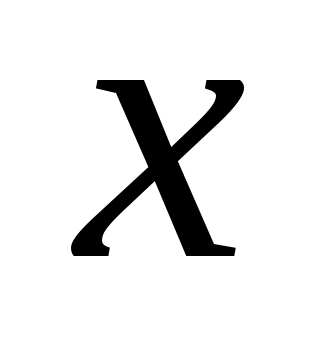 , изменяясь, принимает любые значения. , изменяясь, принимает любые значения.
Определение. Число  называется пределом функции называется пределом функции 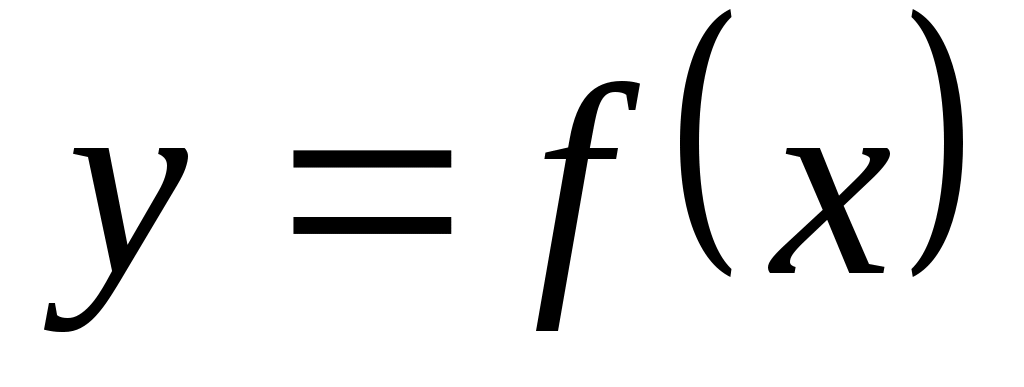 при при 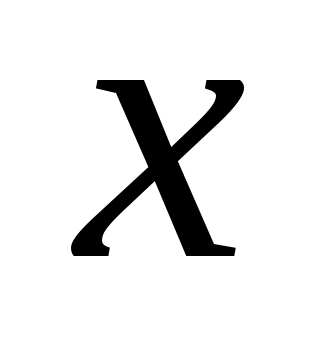 стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа 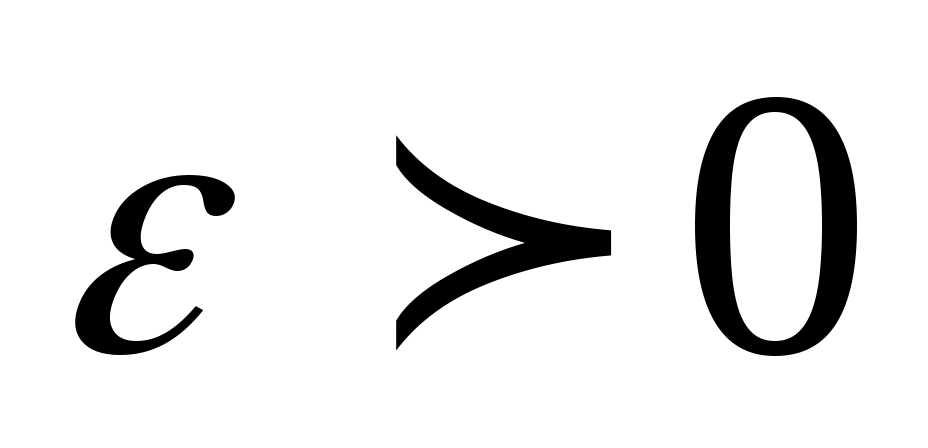 , найдется такое положительное число , найдется такое положительное число 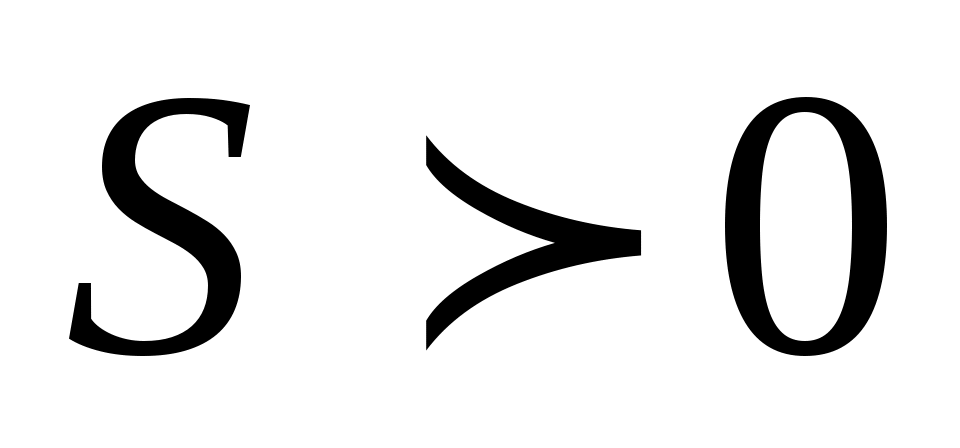 (зависящее от (зависящее от 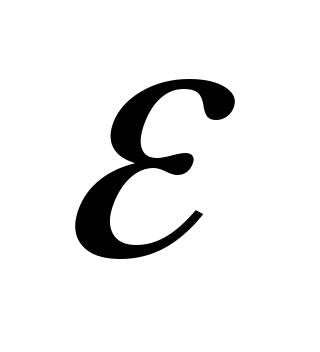 ), что для всех ), что для всех 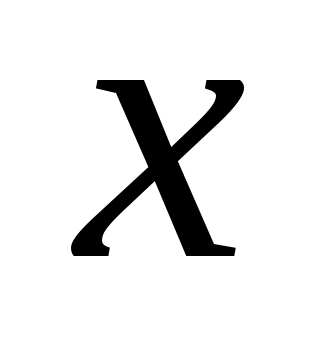 таких что таких что 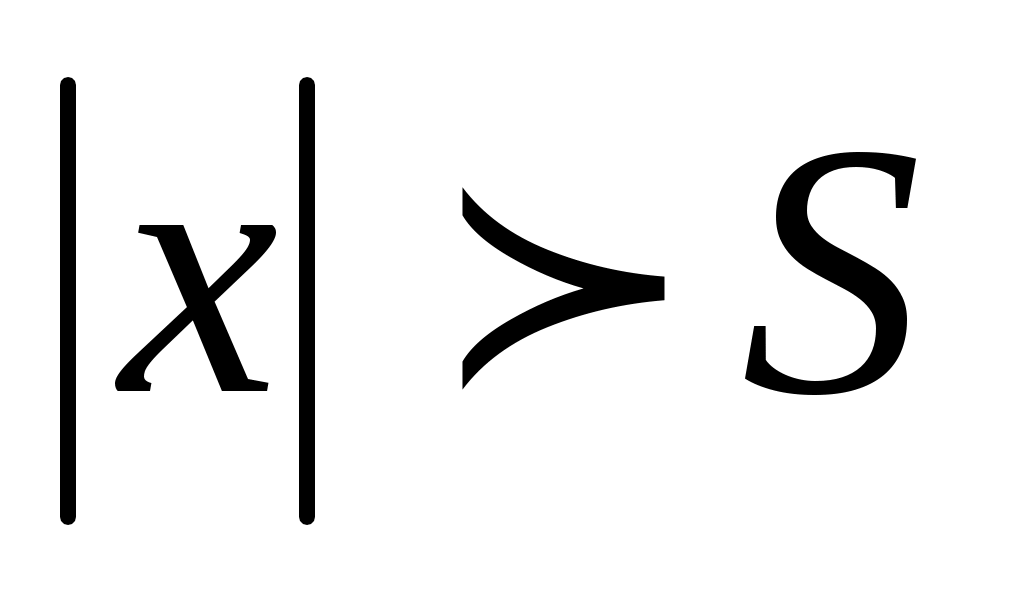 , верно неравенство: , верно неравенство:
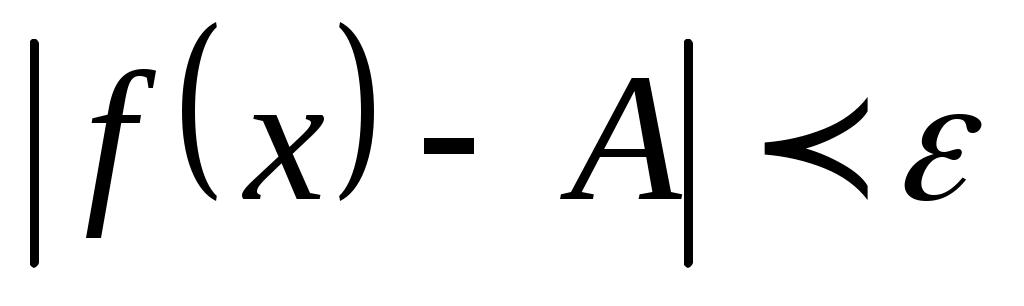 . .
Это предел функции обозначается: 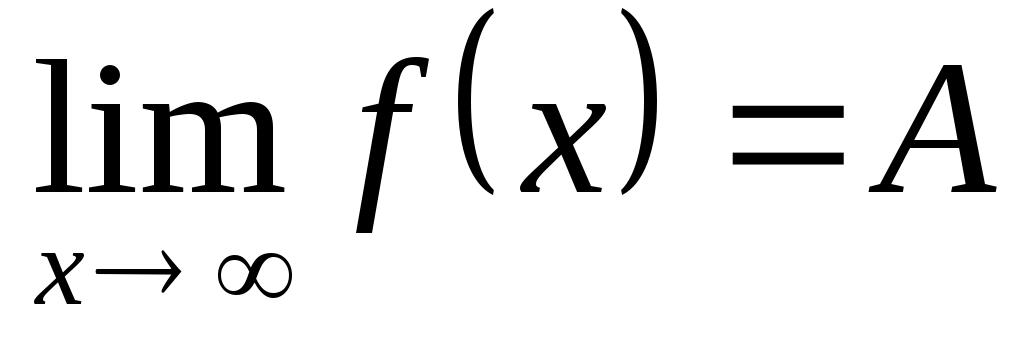 или или 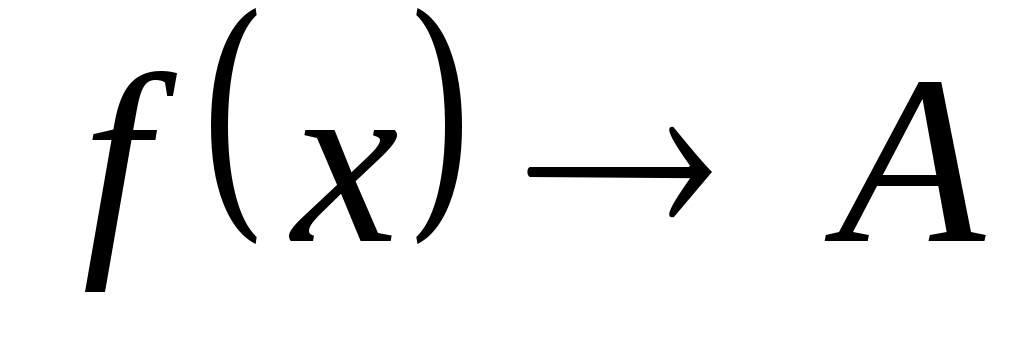 при при  . .
Можно сформулировать понятие предела при стремлении 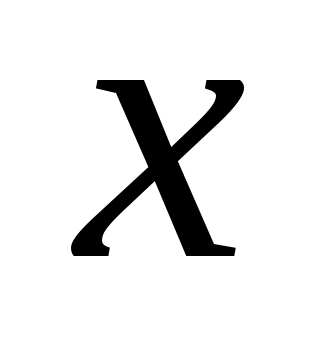 к бесконечности определенного знака, т.е. при к бесконечности определенного знака, т.е. при  и при и при 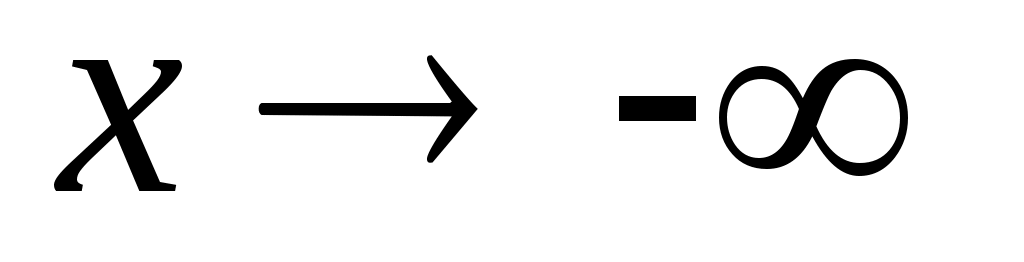 . В первом случае основное неравенство: . В первом случае основное неравенство: 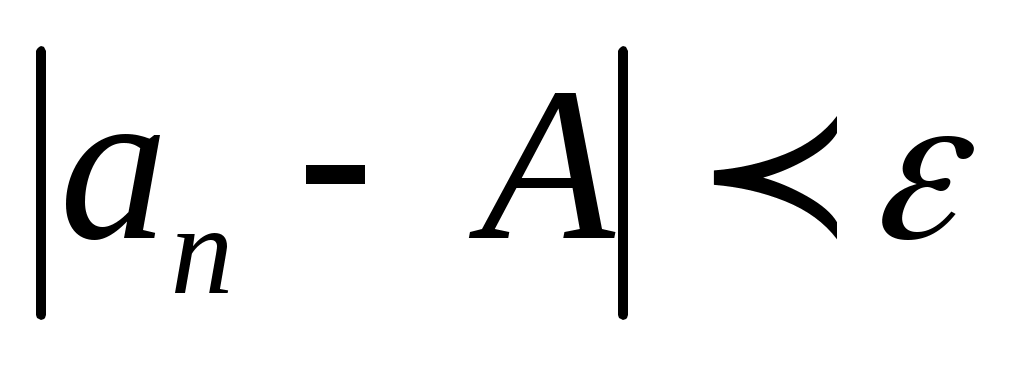 должно выполнятся для всех должно выполнятся для всех 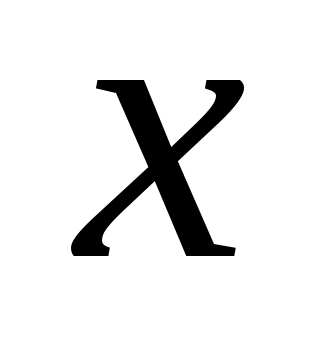 таких, что таких, что 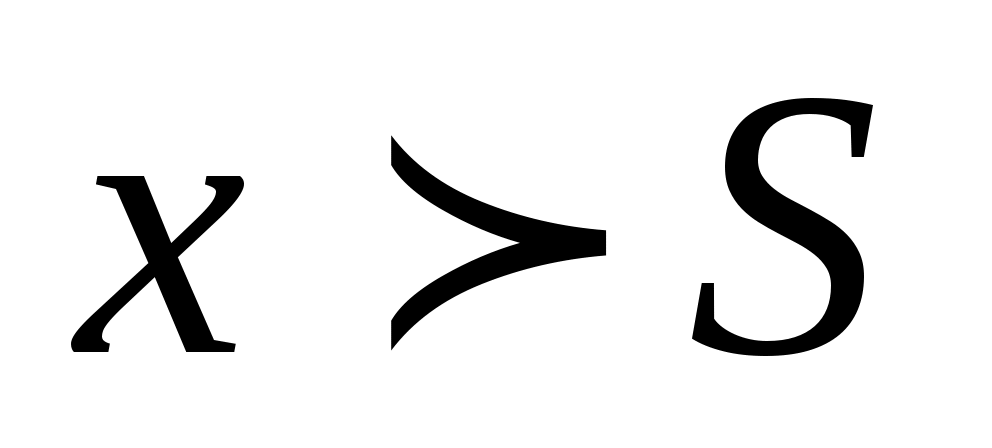 , а во втором – для всех , а во втором – для всех 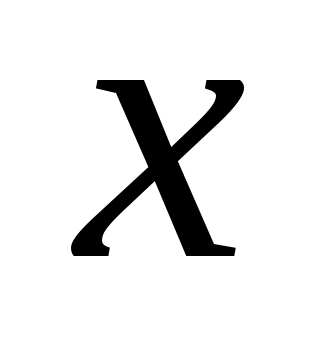 таких, что таких, что 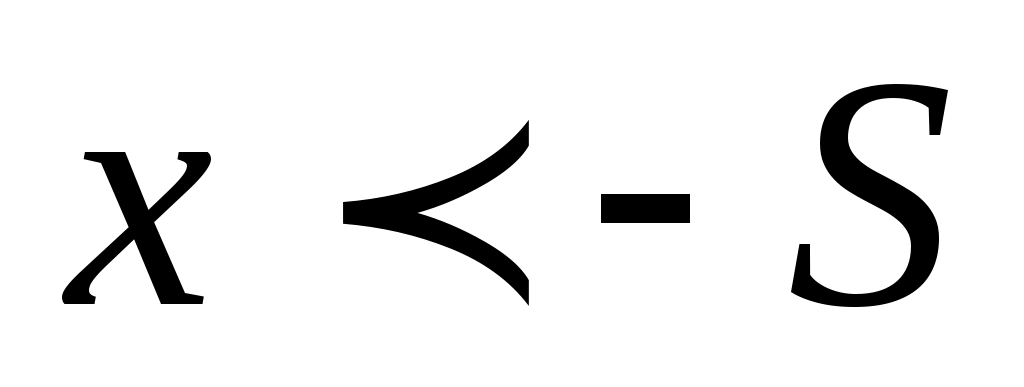 . .
Предел функции в точке: Пусть функция 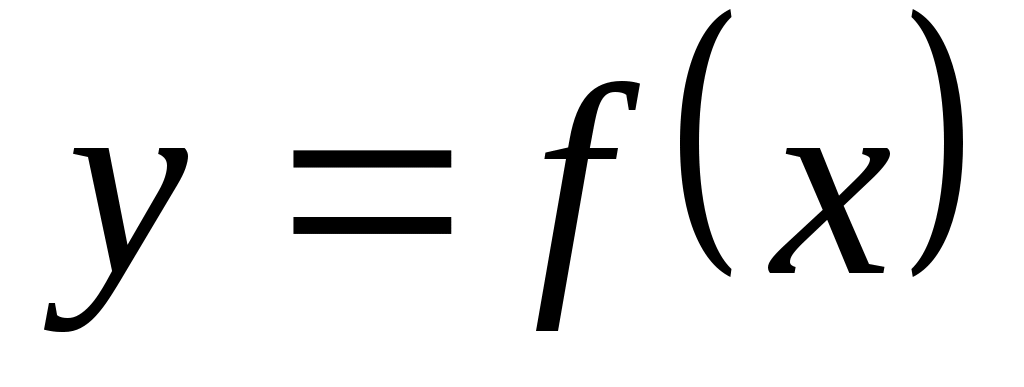 задана в некоторой окрестности точки задана в некоторой окрестности точки 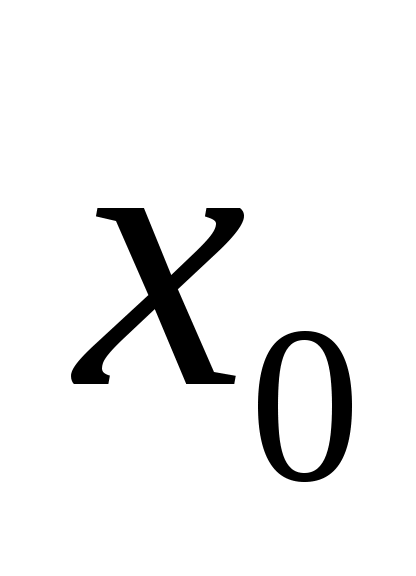 , кроме, быть может, самой точки , кроме, быть может, самой точки 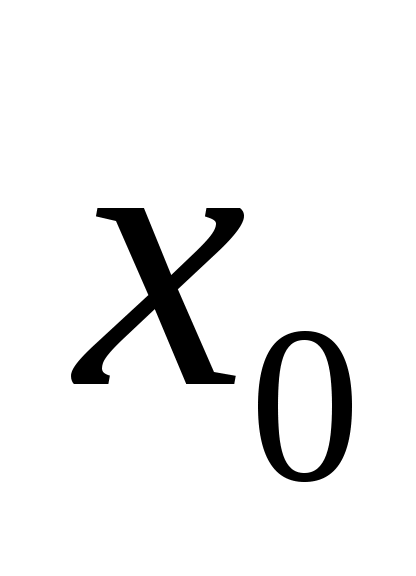 . .
Определение. Число  называется пределом функции называется пределом функции 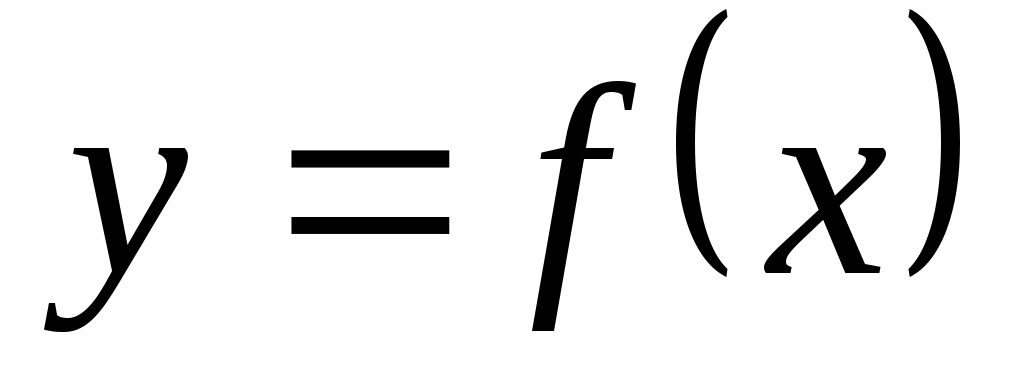 при при 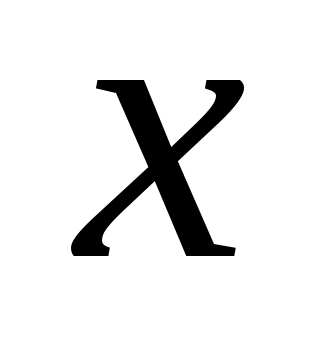 стремящемся к стремящемся к 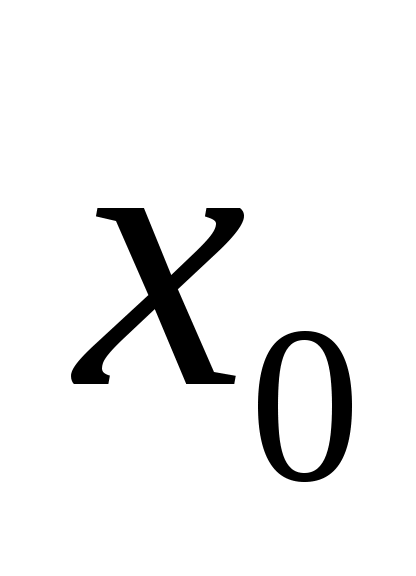 (или в точке (или в точке 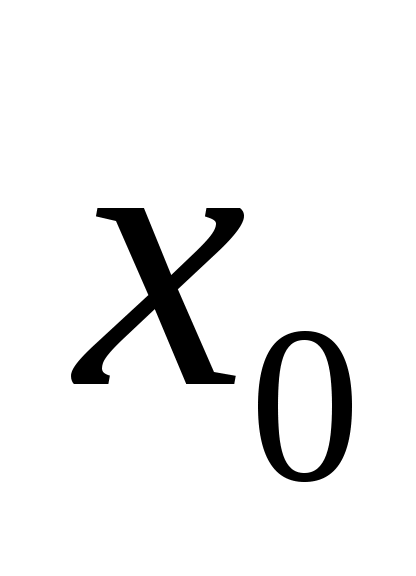 ), если для любого, даже сколько угодно малого положительного числа ), если для любого, даже сколько угодно малого положительного числа 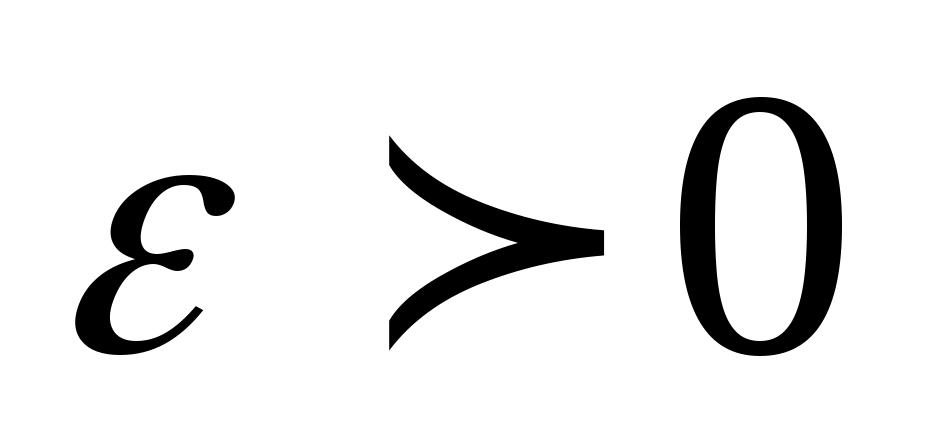 , найдется такое положительное число , найдется такое положительное число 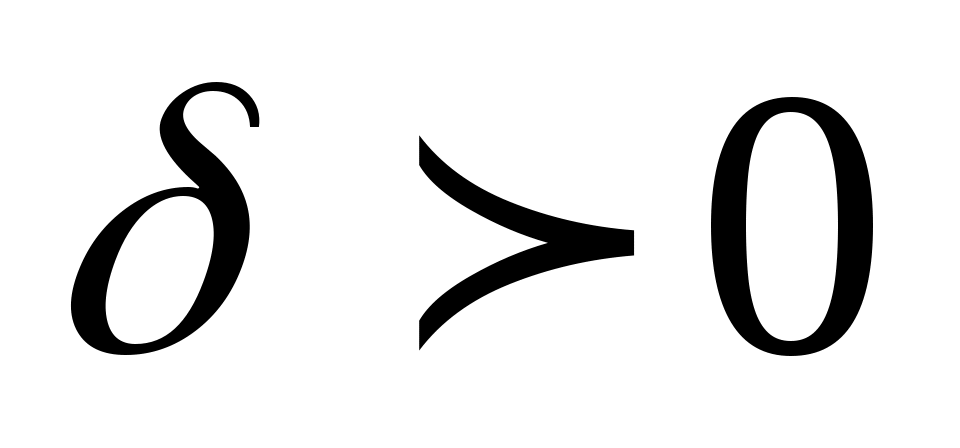 (зависящее от (зависящее от 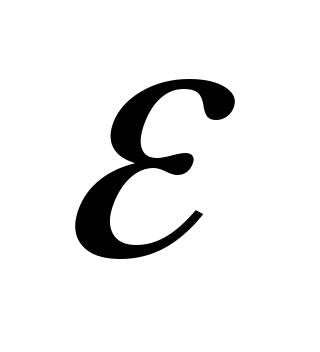 ), что для всех ), что для всех 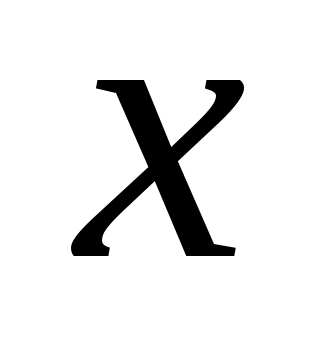 , не равных , не равных 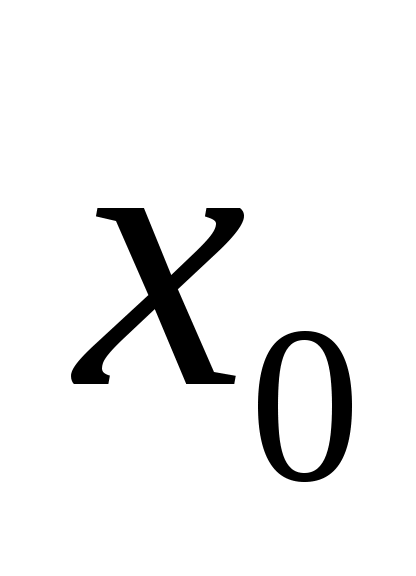 и удовлетворяющих условию и удовлетворяющих условию 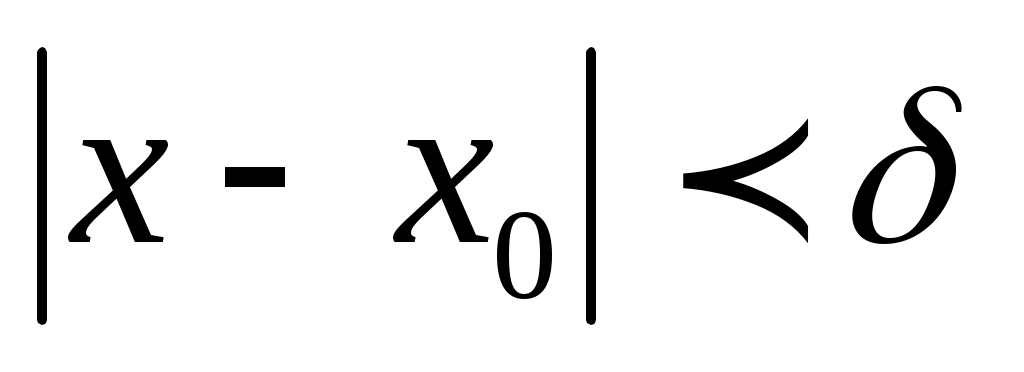 , выполняется неравенство , выполняется неравенство 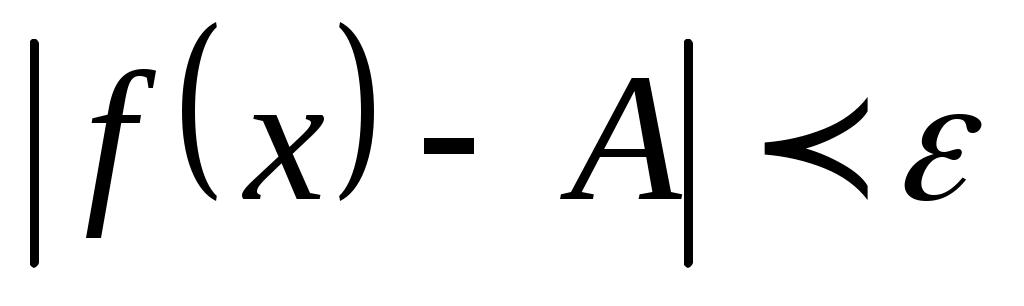 . .
Это предел функции обозначается: 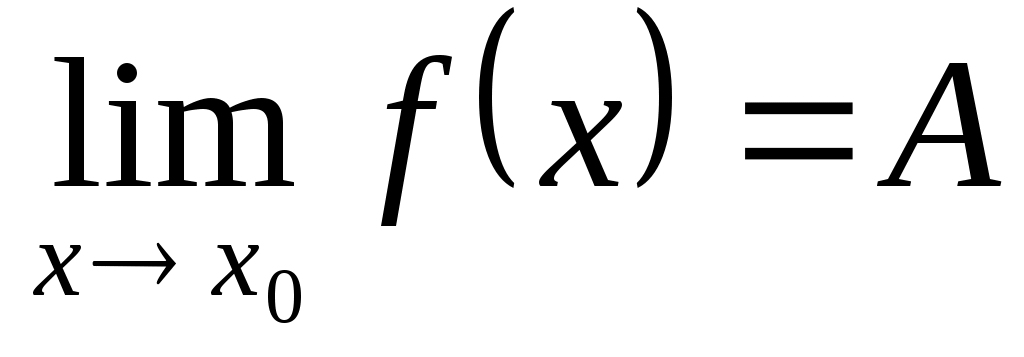 или или 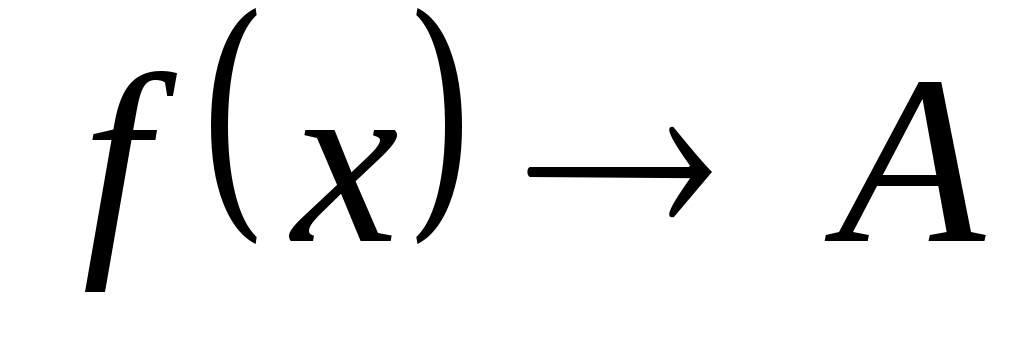 при при 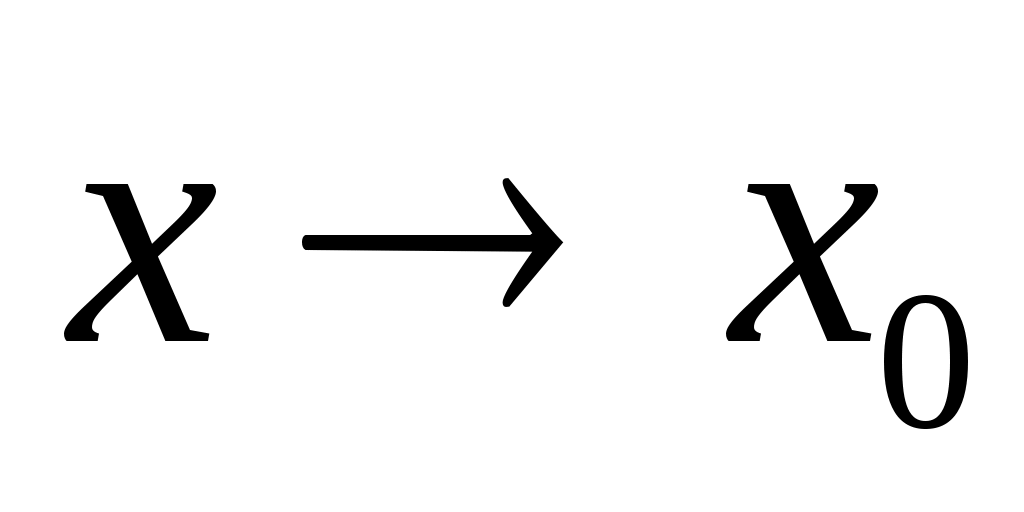 . .
Если при стремлении 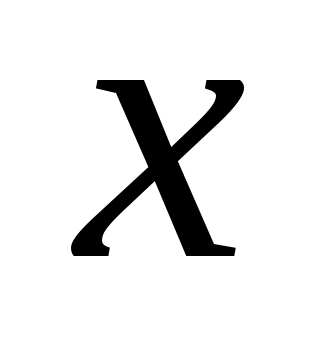 к к 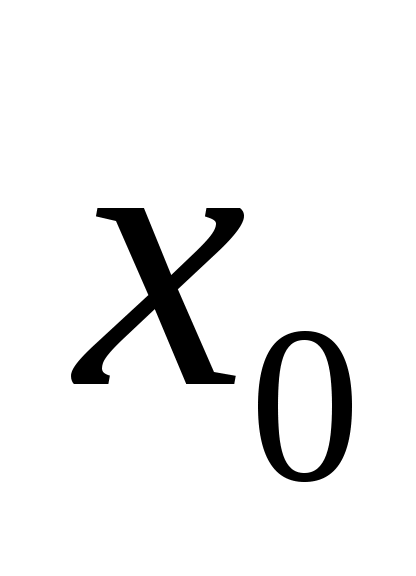 переменная переменная 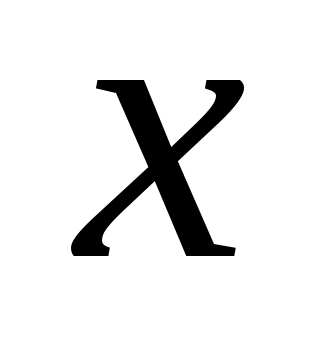 принимает лишь значения, меньшие принимает лишь значения, меньшие 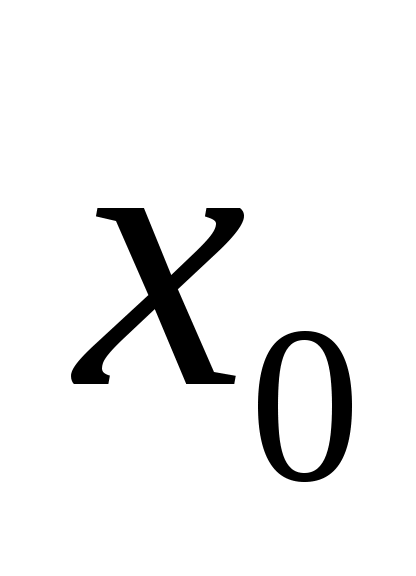 , или наоборот, лишь значения большие , или наоборот, лишь значения большие 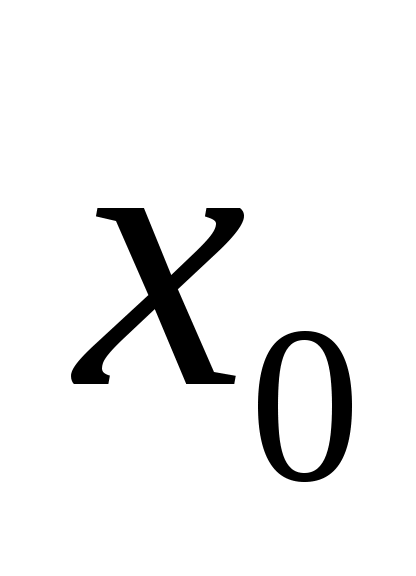 , и при этом функция , и при этом функция 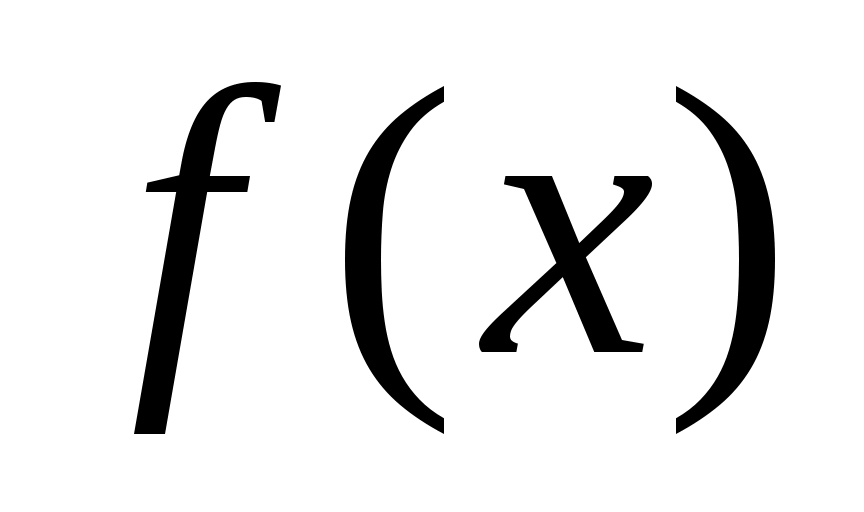 стремится к некоторому числу стремится к некоторому числу  , то говорят об односторонних пределах функции , то говорят об односторонних пределах функции 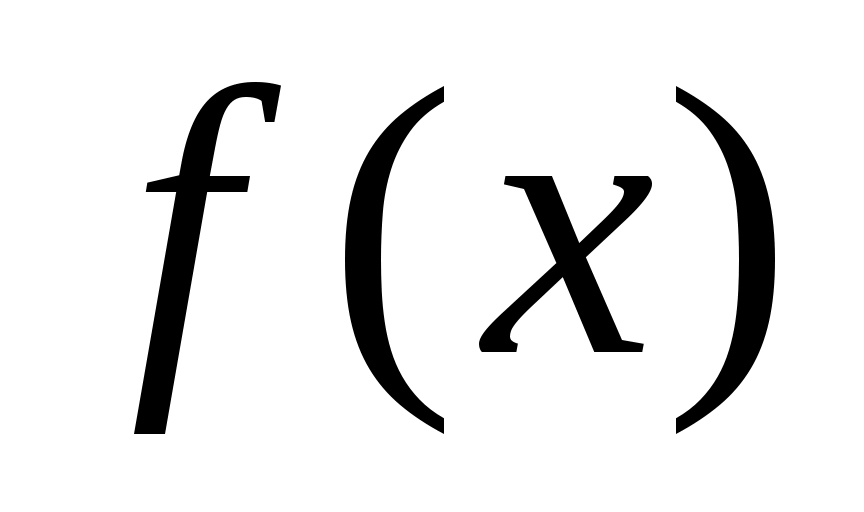 соответственно слева соответственно слева 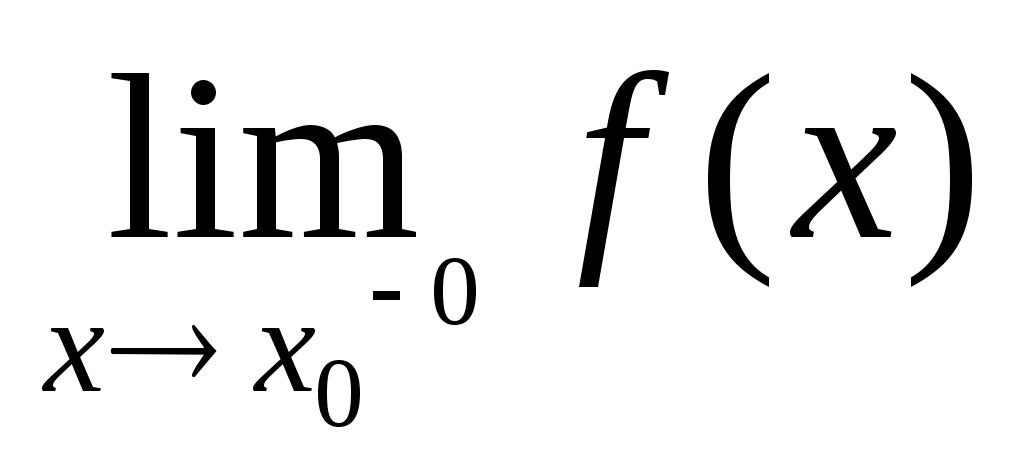 и справа и справа 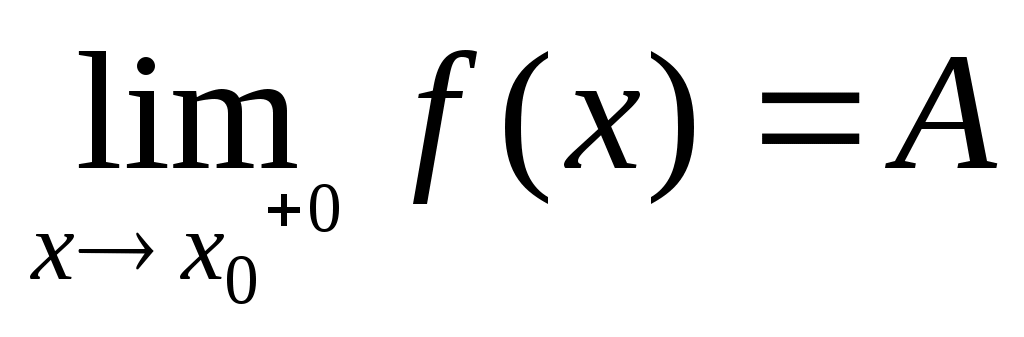 . .
Признаки существования предела
Теорема 1. Если числовая последовательность 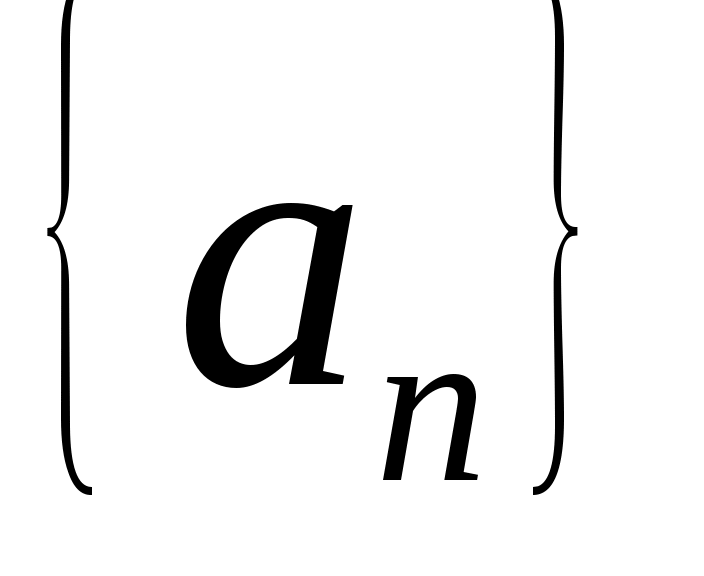 монотонна и ограничена, то она имеет предел. монотонна и ограничена, то она имеет предел.
Теорема 2. Если в некоторой окрестности точки 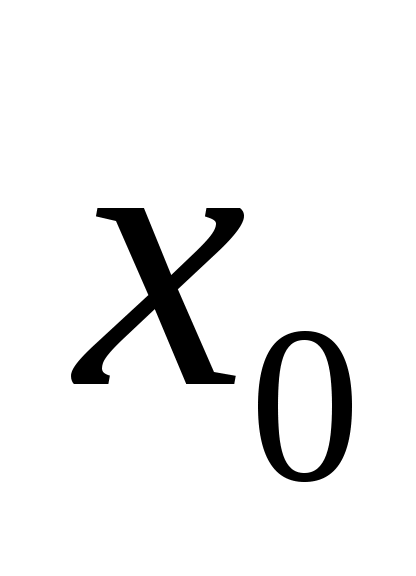 (или при достаточно больших значениях (или при достаточно больших значениях 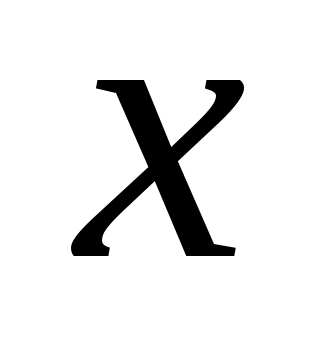 ) функция ) функция 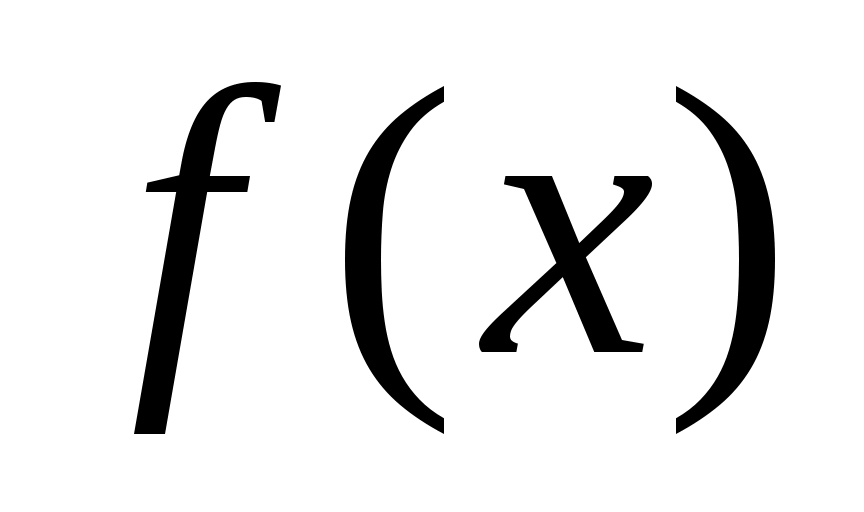 заключена между двумя функциями заключена между двумя функциями 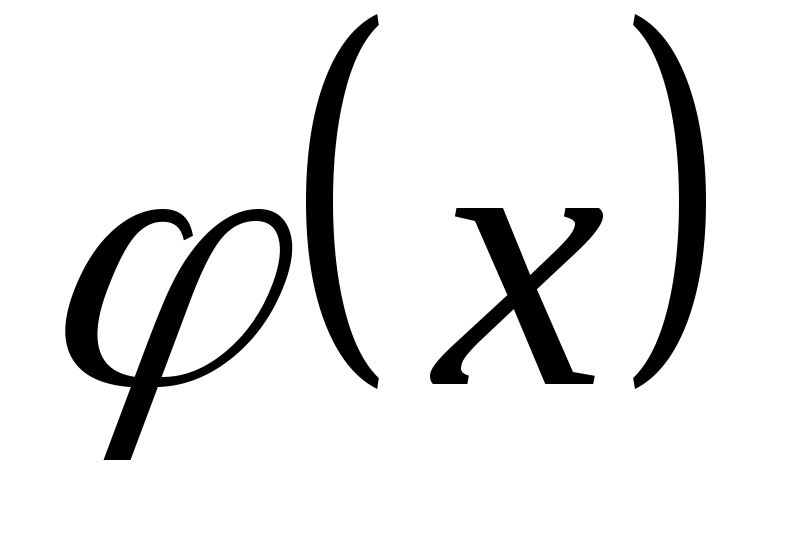 и и 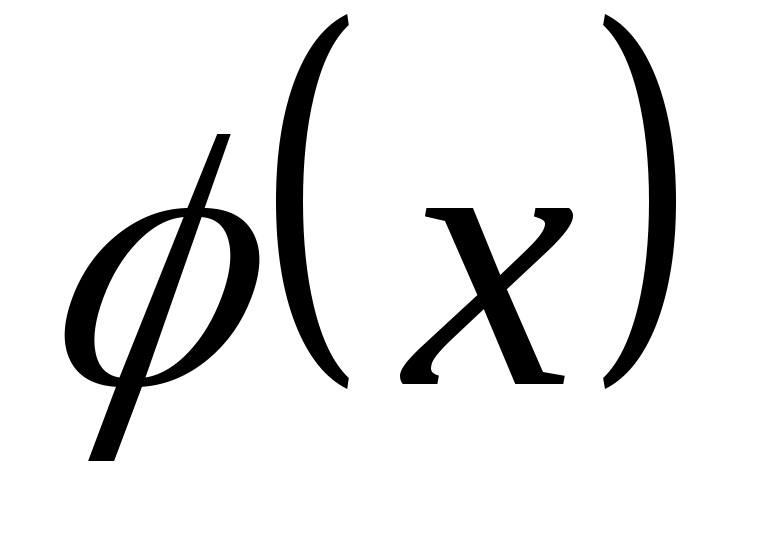 , имеющими одинаковый предел , имеющими одинаковый предел  при при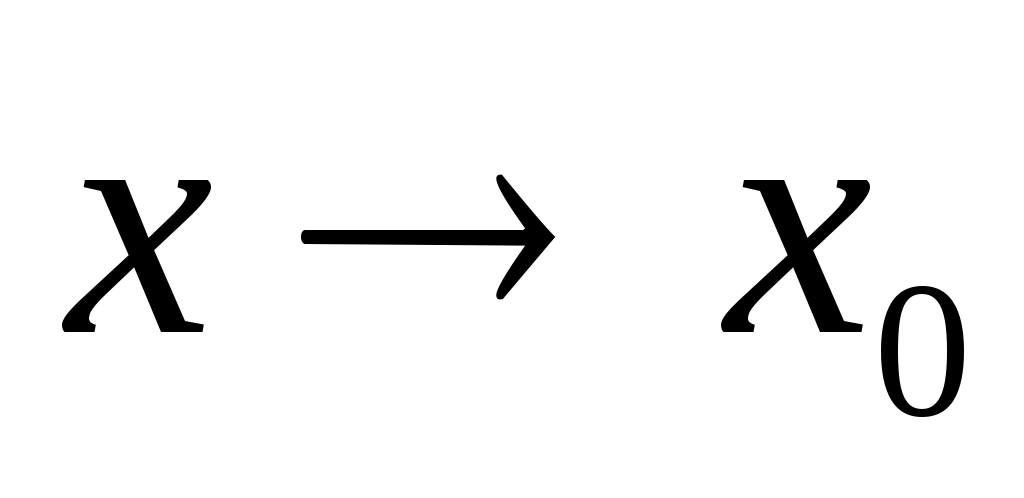 (или (или  ), то функция ), то функция 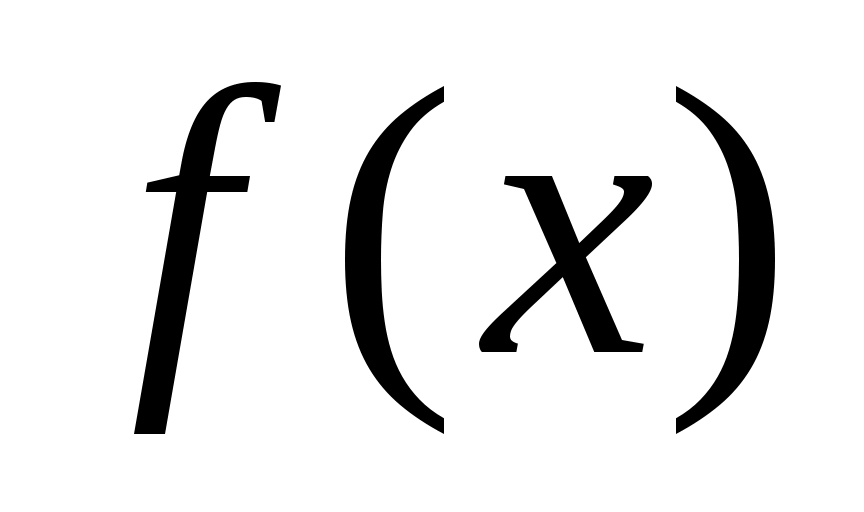 имеет тот же предел имеет тот же предел  . .
Пусть при 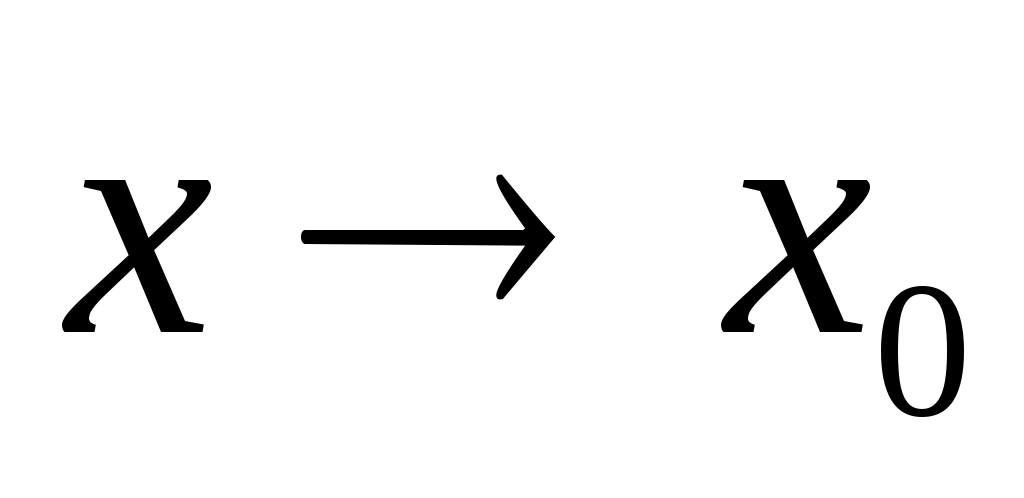 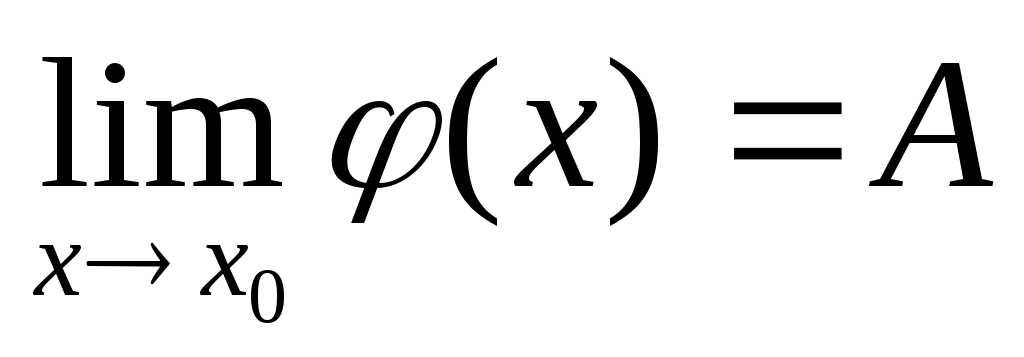 , , 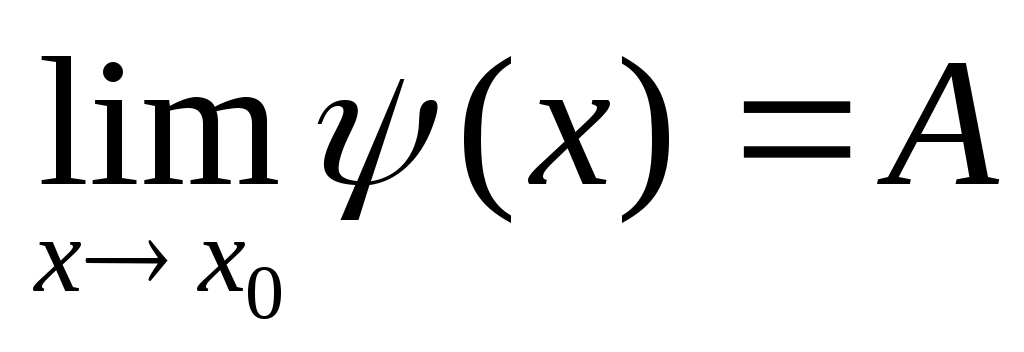 . .
Это означает, что для любого 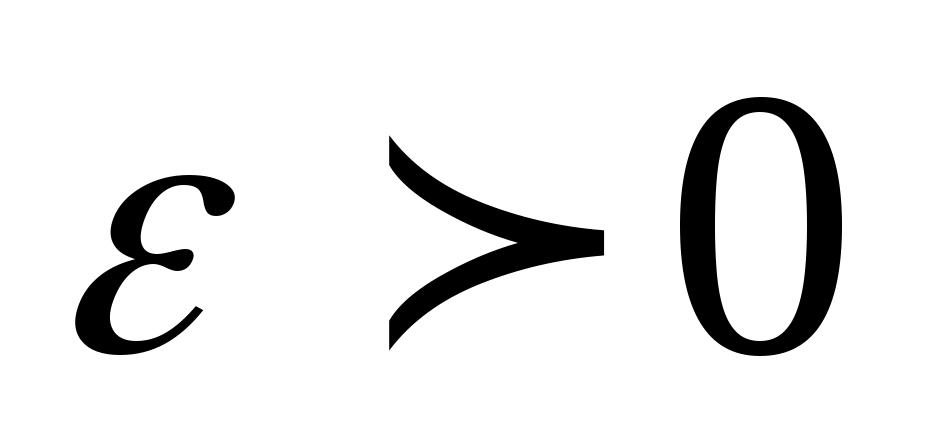 найдется такое число найдется такое число 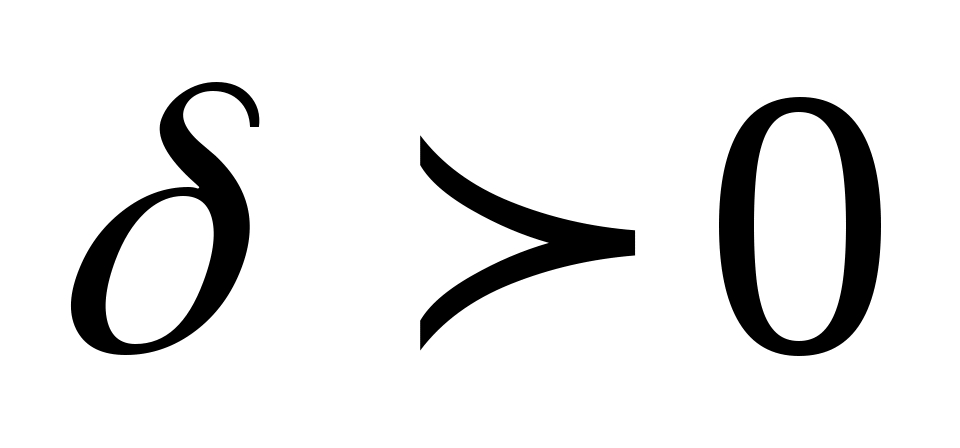 , что для всех , что для всех 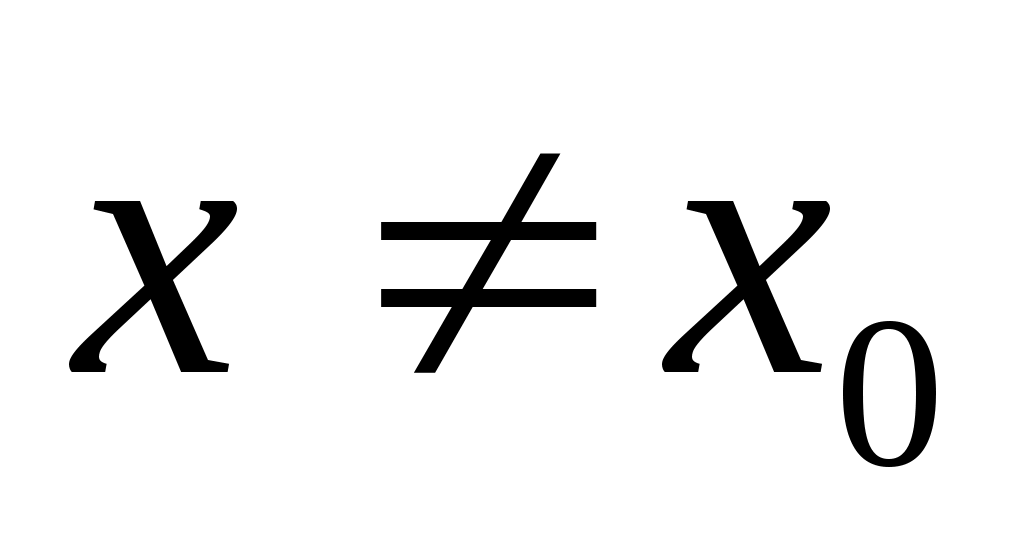 и удовлетворяющих условию и удовлетворяющих условию 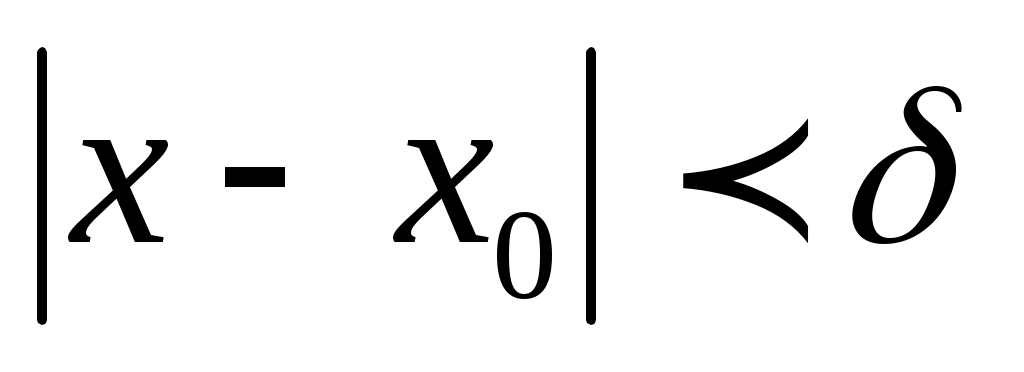 будут верны одновременно неравенства: будут верны одновременно неравенства:
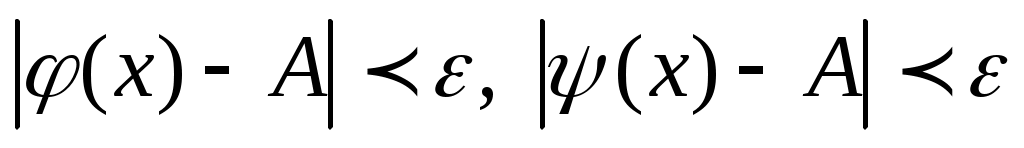 (1.1) (1.1)
или
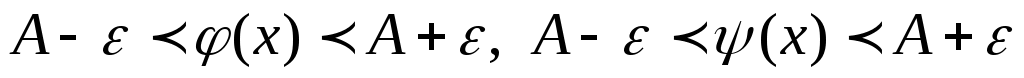
Т.к. по условию функция 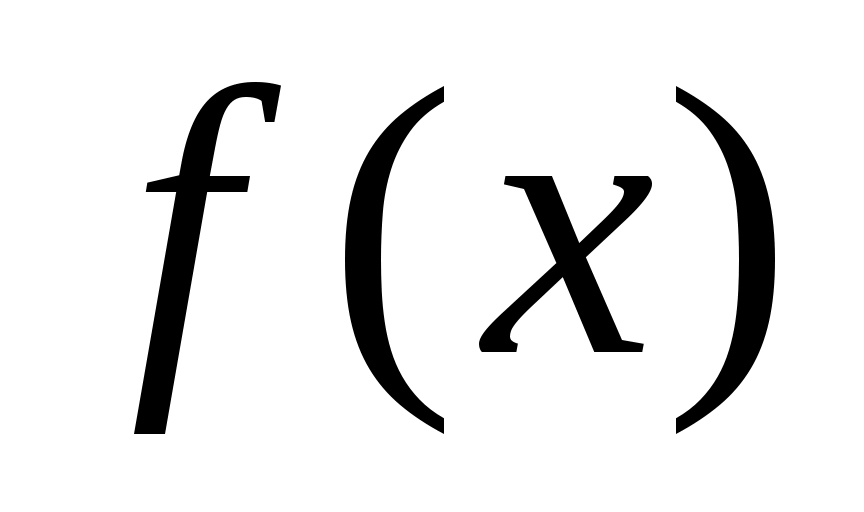 заключена между двумя функциями, т.е.: заключена между двумя функциями, т.е.:
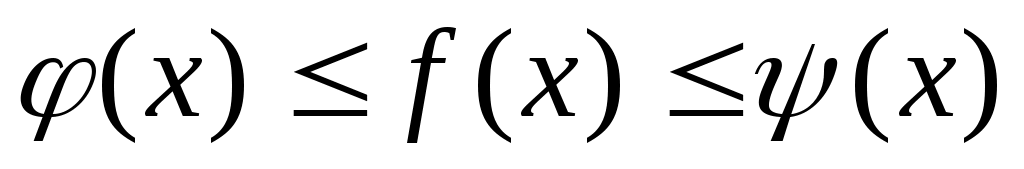 , то из неравенств (1.1) следует, что , то из неравенств (1.1) следует, что 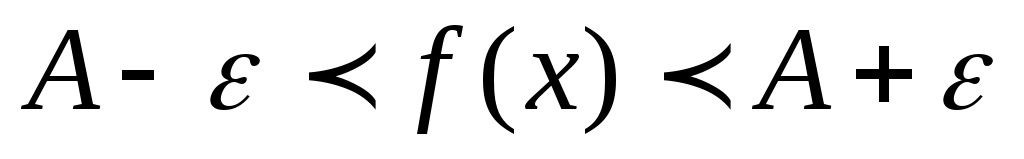 , т.е.: , т.е.:
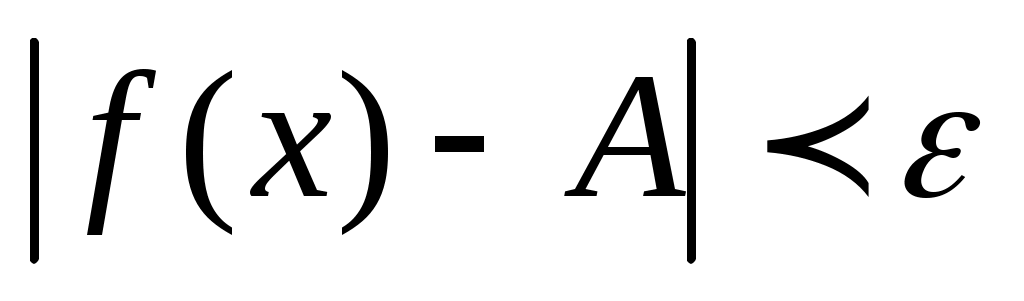 . .
А это и означает, что 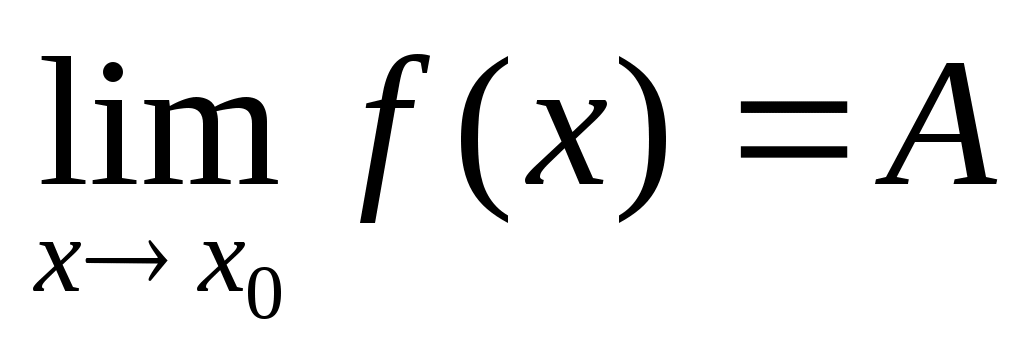
17. Определение предела функции в точке. Основные теоремы о пределах (одну из них доказать).
Предел функции в точке
Определение. Число  называется пределом функции называется пределом функции 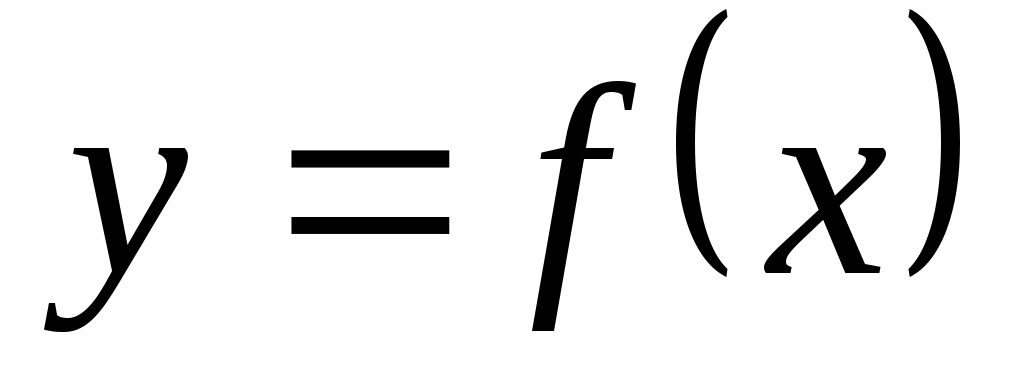 при при 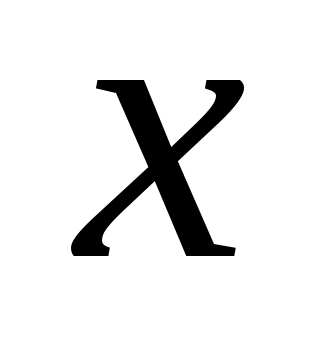 стремящемся к стремящемся к 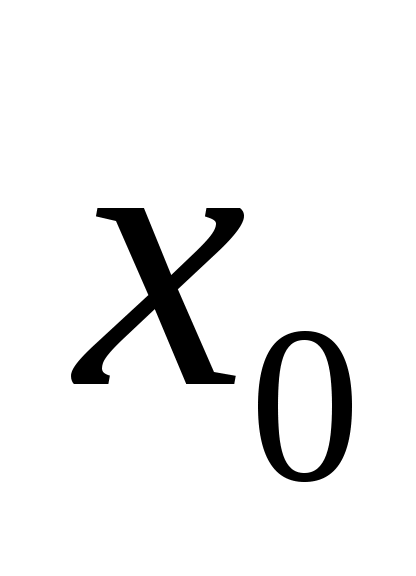 (или в точке (или в точке 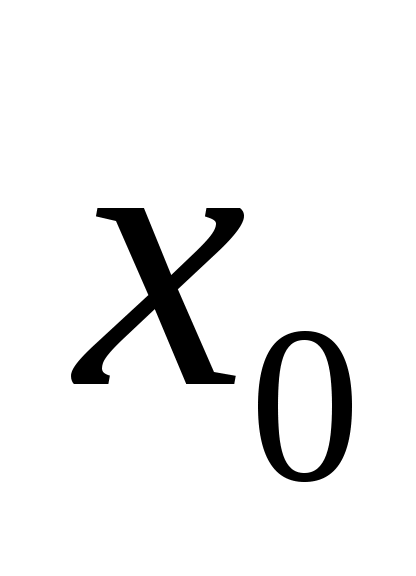 ), если для любого, даже сколько угодно малого положительного числа ), если для любого, даже сколько угодно малого положительного числа 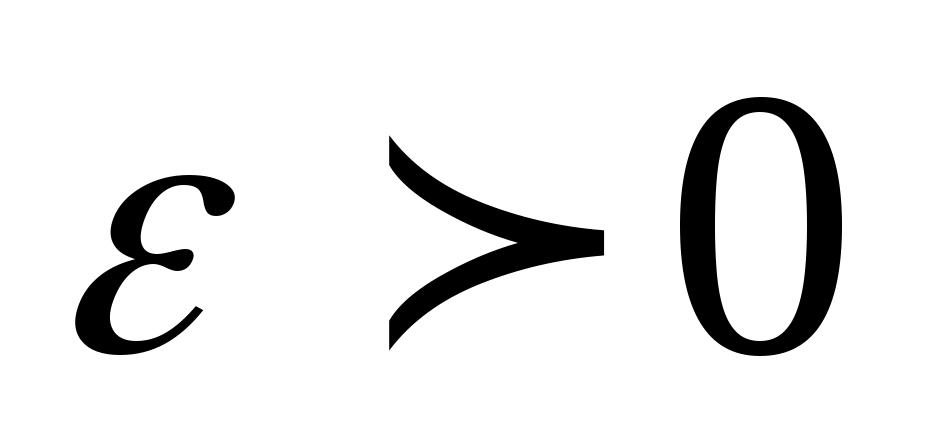 , найдется такое положительное число , найдется такое положительное число 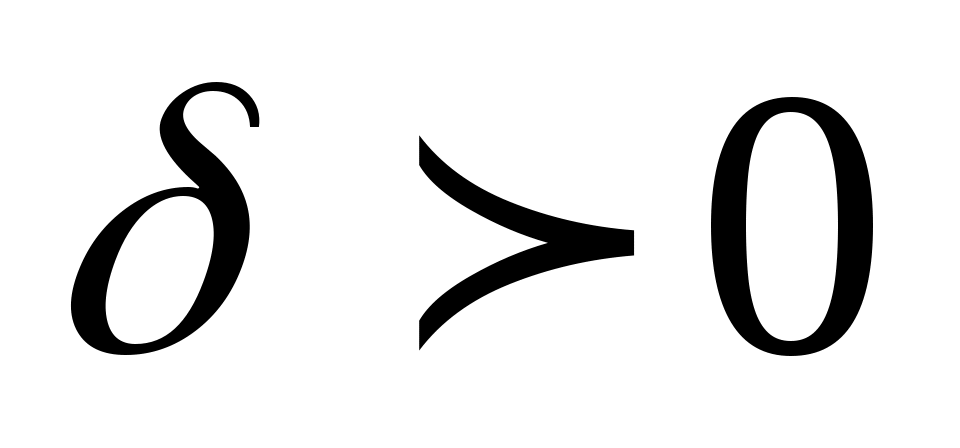 (зависящее от (зависящее от 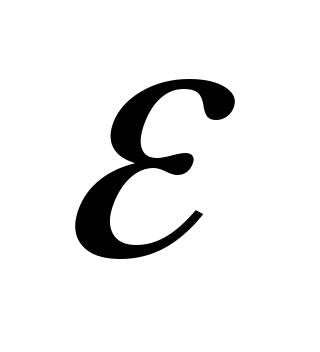 ), что для всех ), что для всех 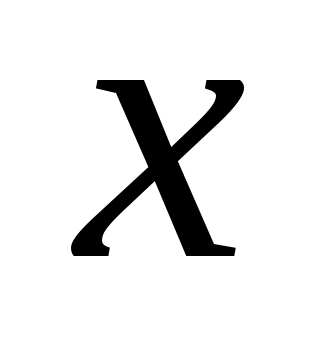 , не равных , не равных 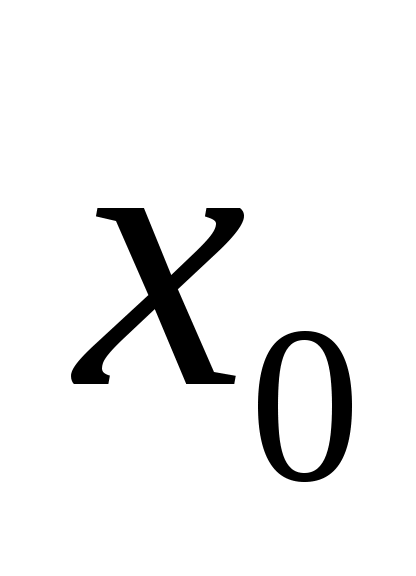 и удовлетворяющих условию и удовлетворяющих условию 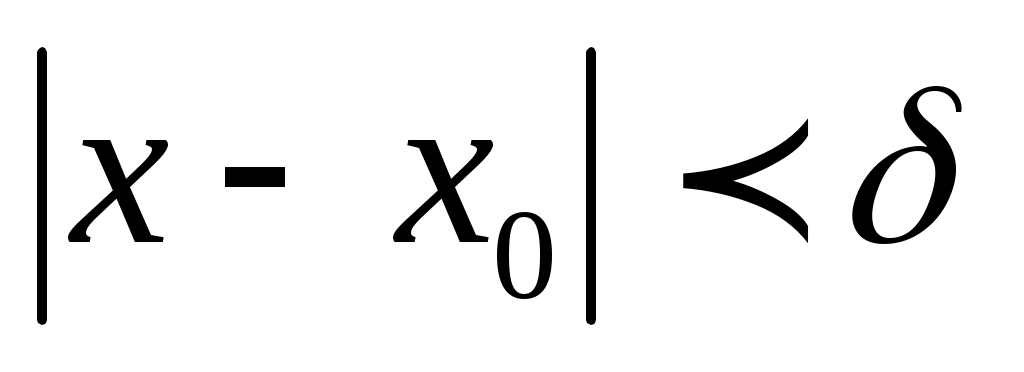 , выполняется неравенство , выполняется неравенство 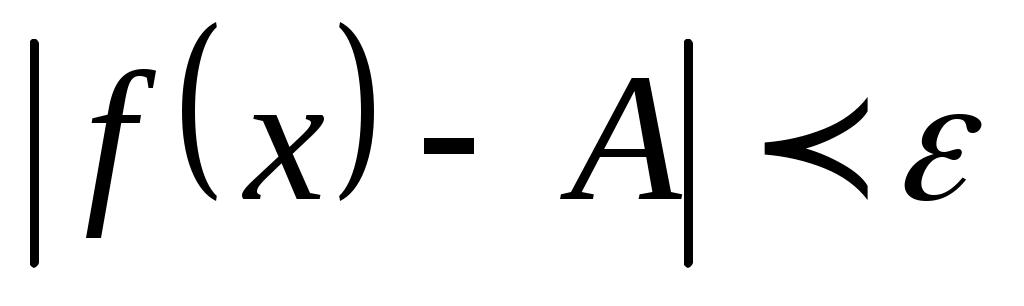 . .
Это предел функции обозначается: 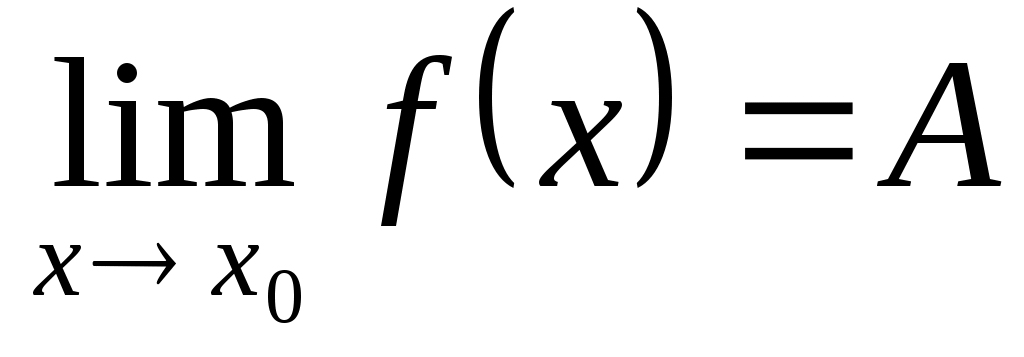 или или 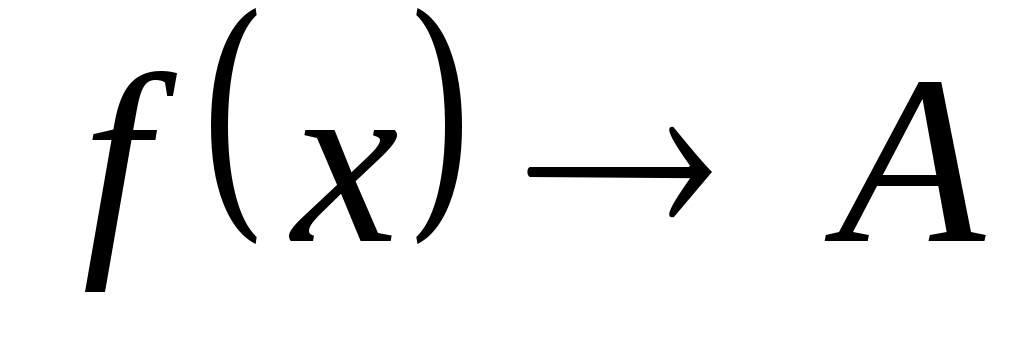 при при 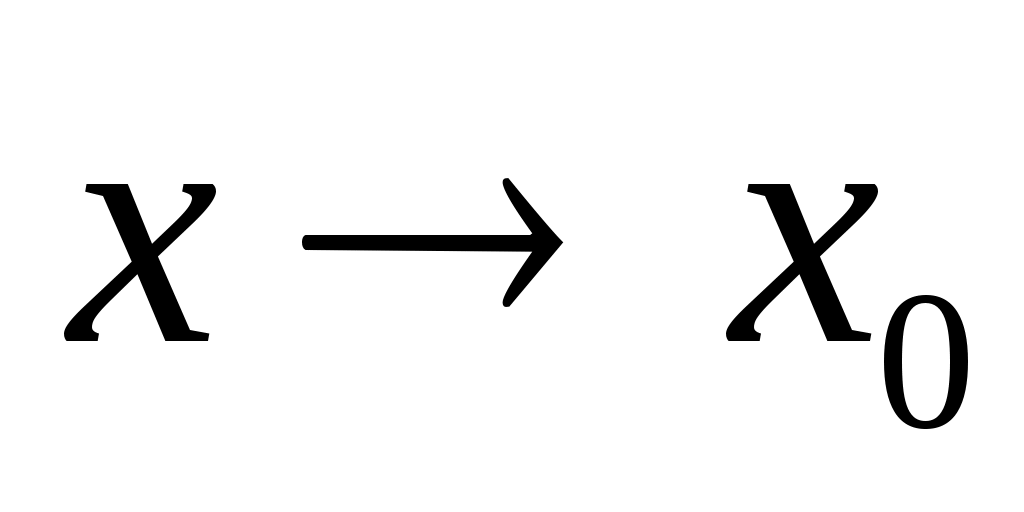 . .
Основные теоремы о пределах. Признаки существования предела
Пусть 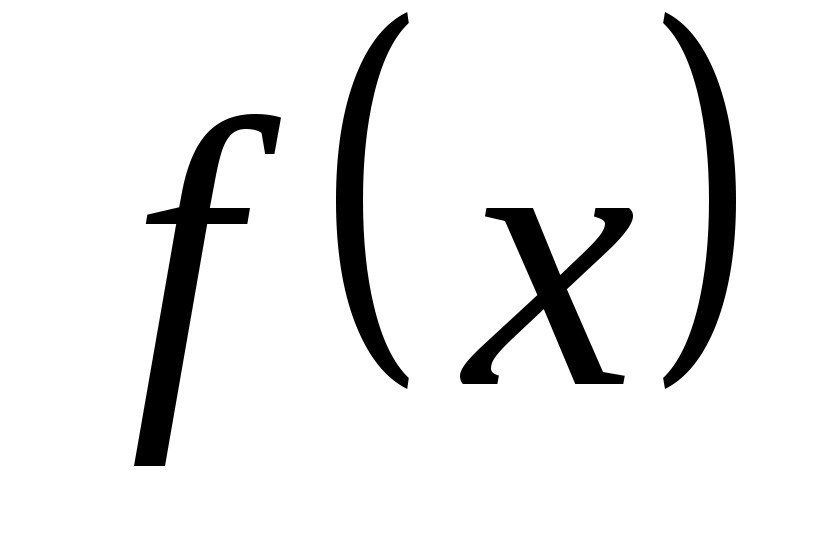 и и 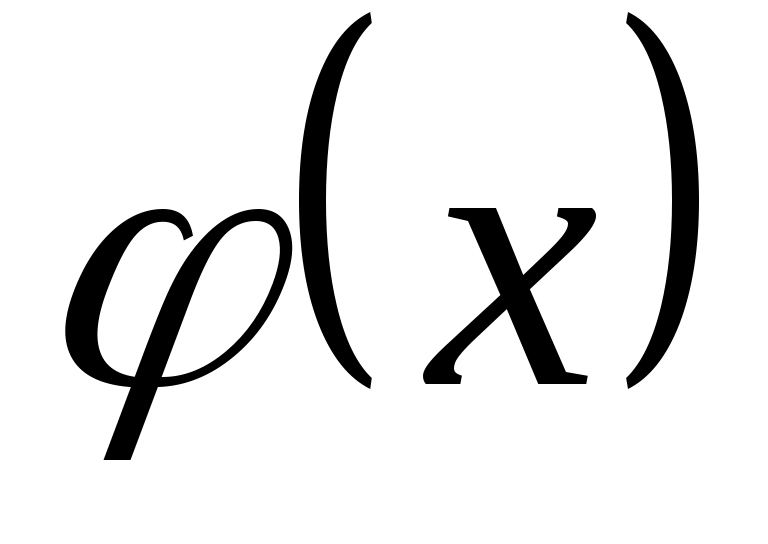 - функции, для которых существуют пределы при - функции, для которых существуют пределы при 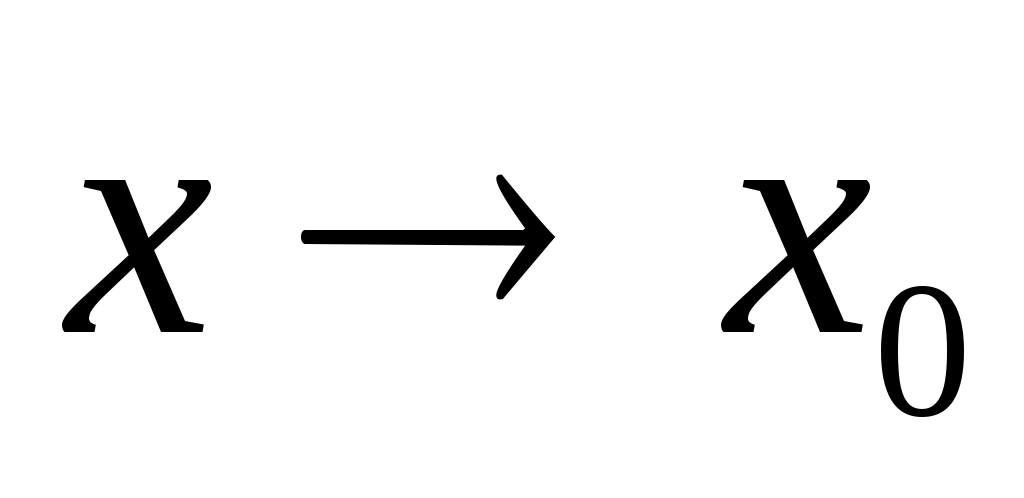 ( ( ): ): 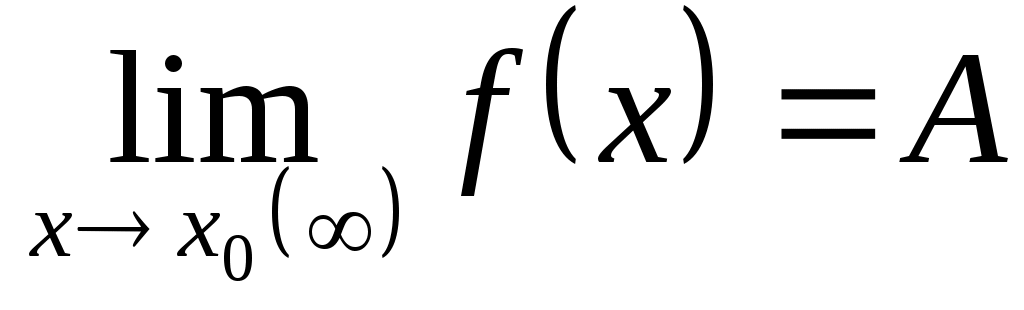 , , 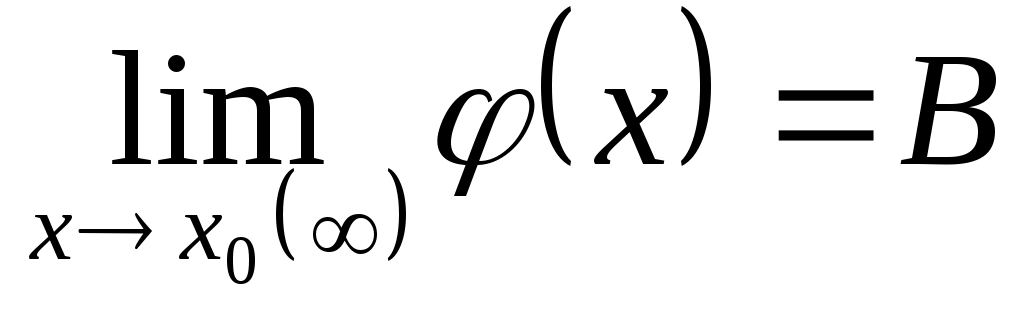 . .
Сформулируем основные теоремы о пределах:
Функция не может иметь более одного предела.
Предположим противное, т.е. что функция 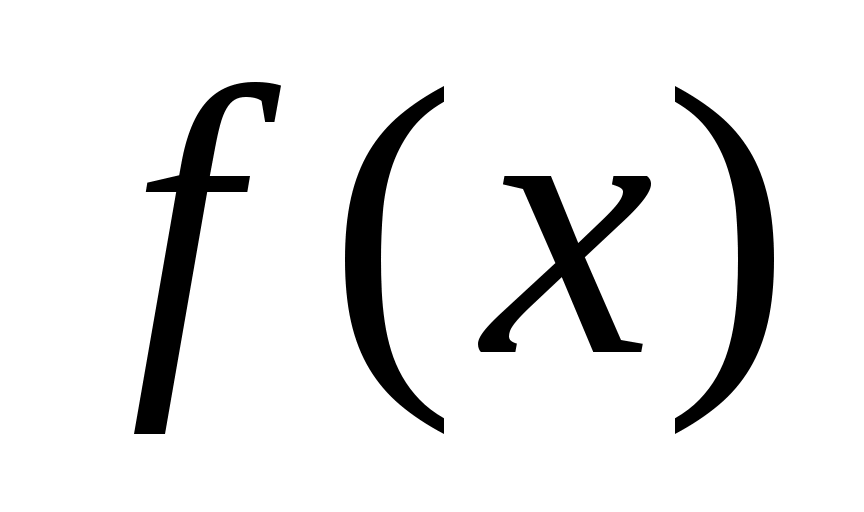 имеет 2 предела А и D, имеет 2 предела А и D, 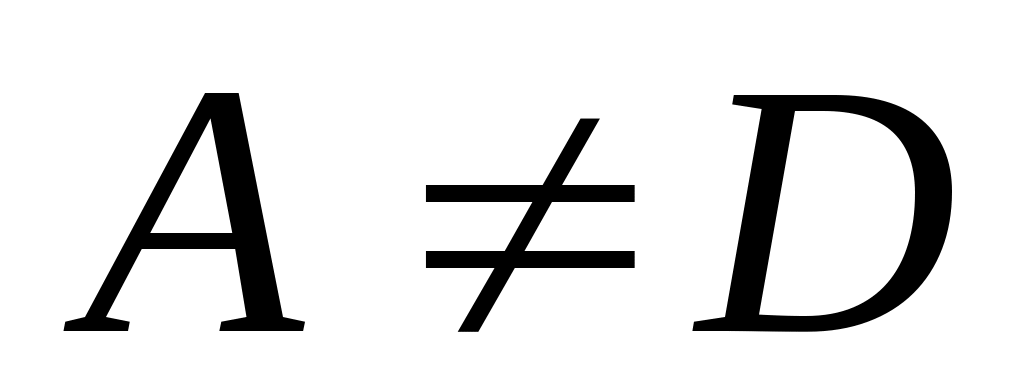 . Тогда на основании теоремы о связи бесконечно малых величин с пределами функции: . Тогда на основании теоремы о связи бесконечно малых величин с пределами функции: 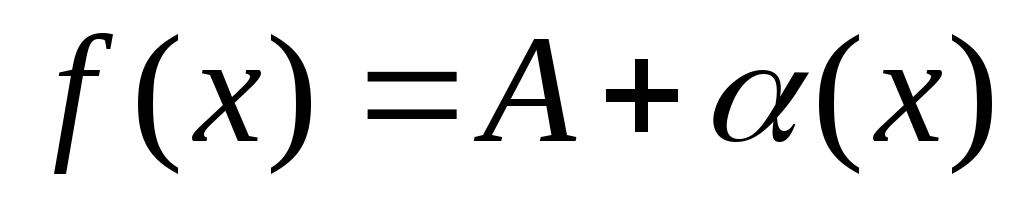 , , 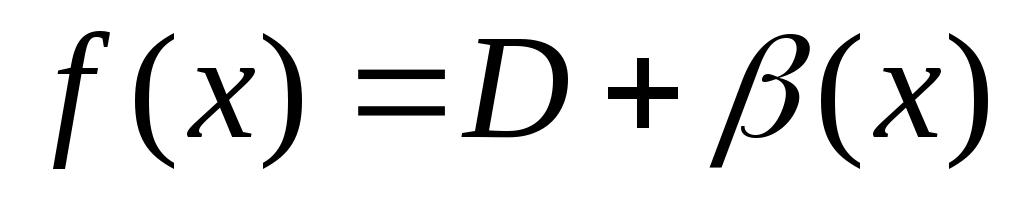 , где , где 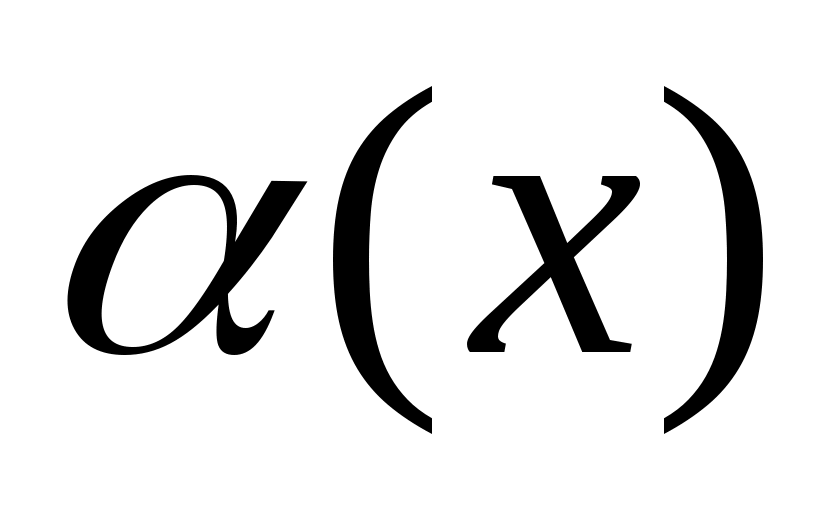 и и 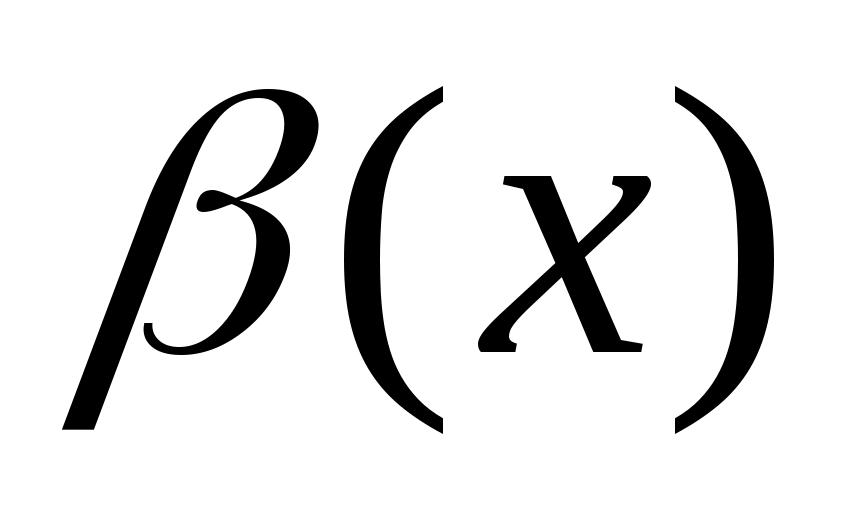 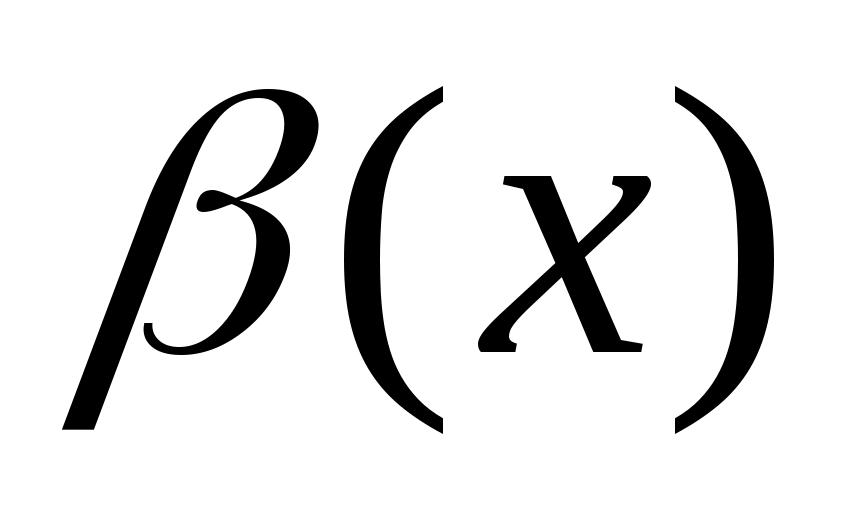 - бесконечно малые величины при - бесконечно малые величины при 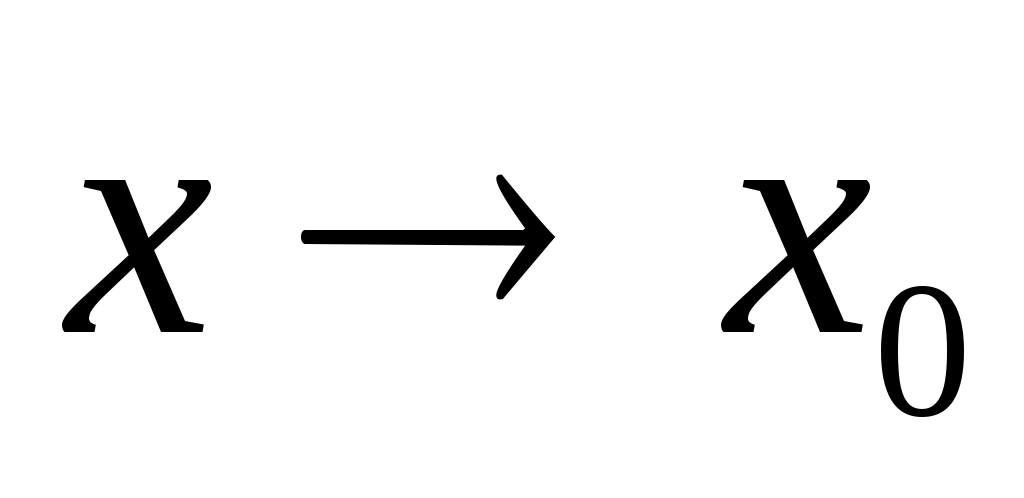 ( ( ). Вычитая почленно эти равенства, получим: ). Вычитая почленно эти равенства, получим: 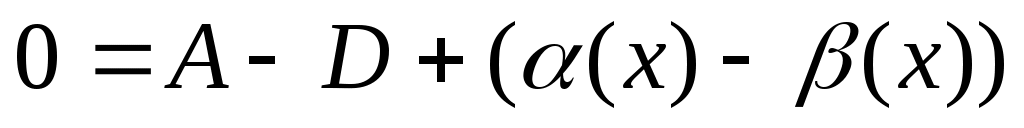 , откуда , откуда 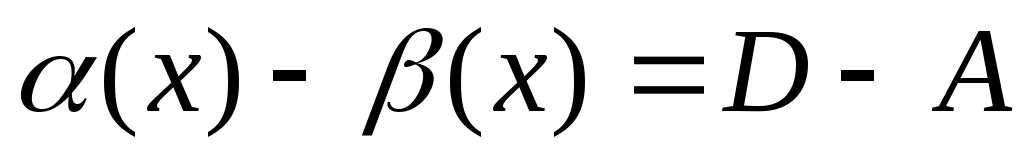 . Это равенство невозможно, т.к. на основании свойства 1 бесконечно малых . Это равенство невозможно, т.к. на основании свойства 1 бесконечно малых 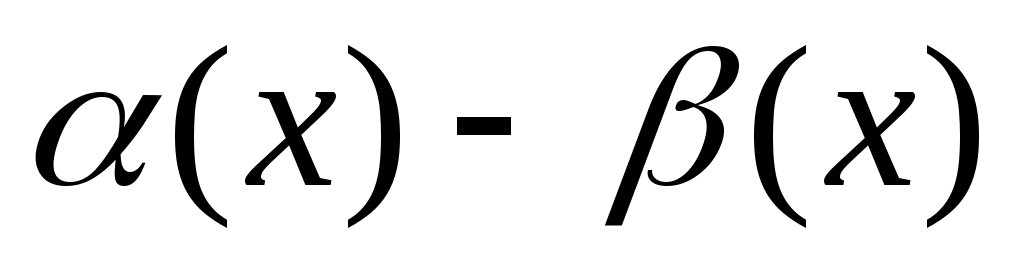 это величина бесконечно малая. Следовательно, предположение о существовании второго предела неверно. это величина бесконечно малая. Следовательно, предположение о существовании второго предела неверно.
Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е.
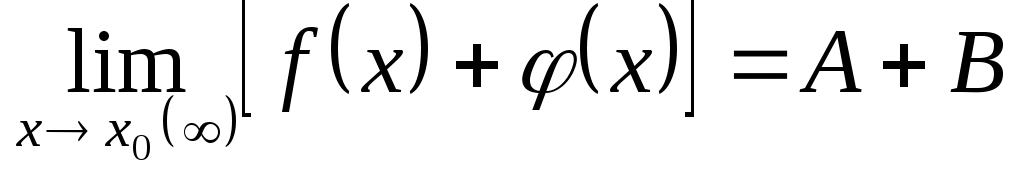 . .
Предел произведения конечного числа функций равен произведению пределов этих функций, т.е.
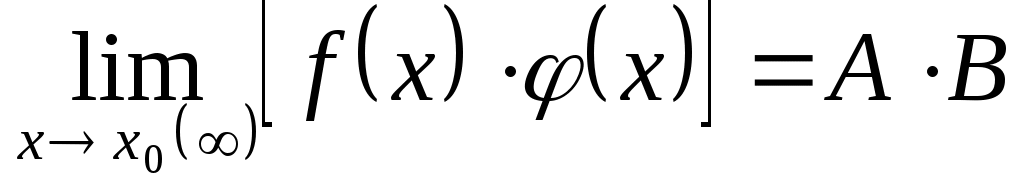 . .
По условию 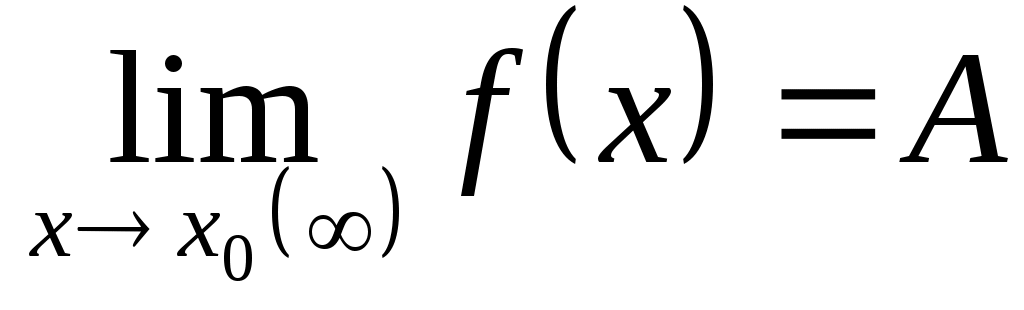 и и 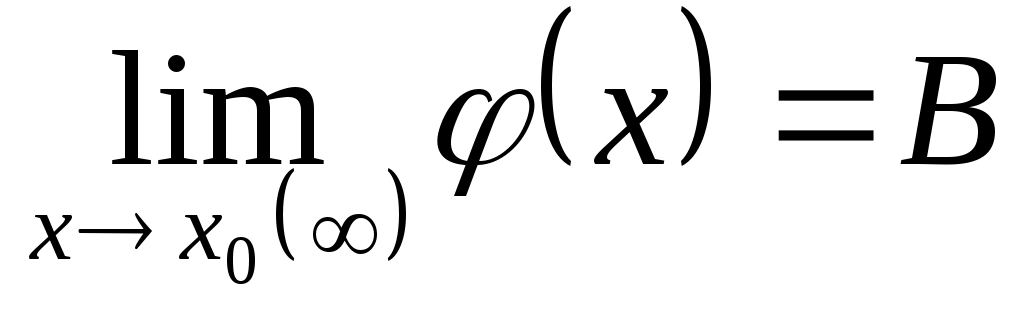 , следовательно, на основании теоремы о связи бесконечно малых величин с пределами функции: , следовательно, на основании теоремы о связи бесконечно малых величин с пределами функции: 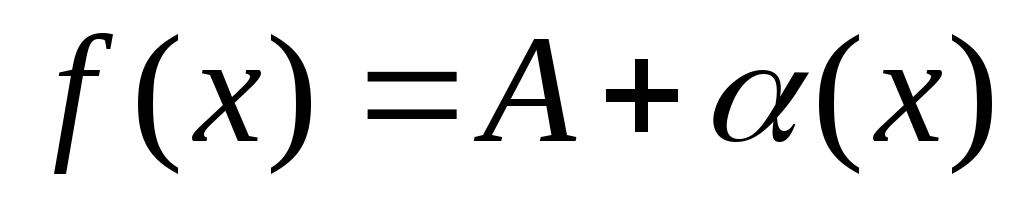 , , 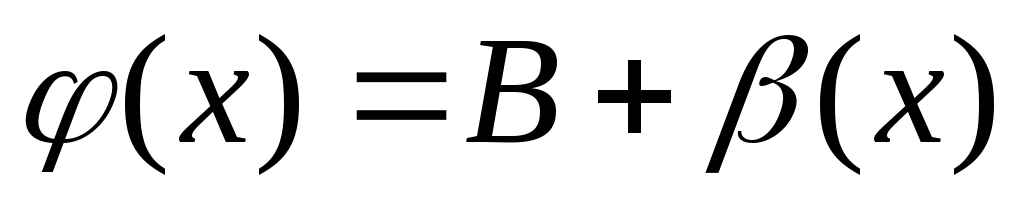 , где , где 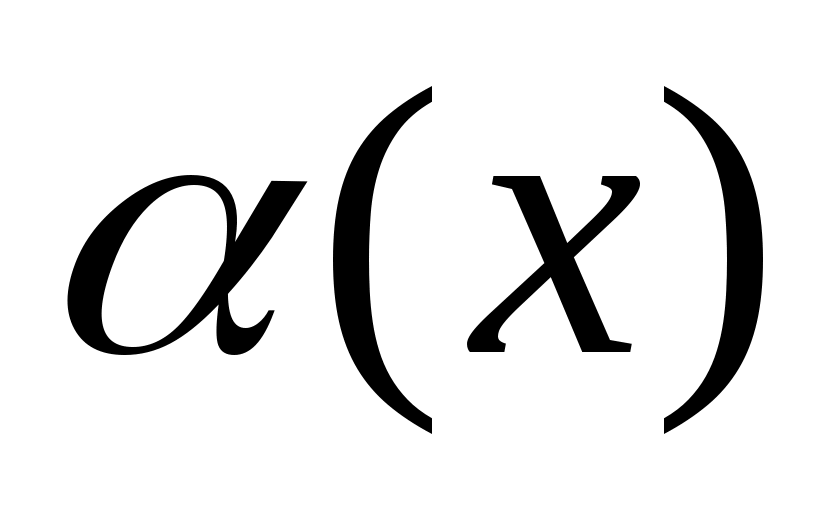 и и 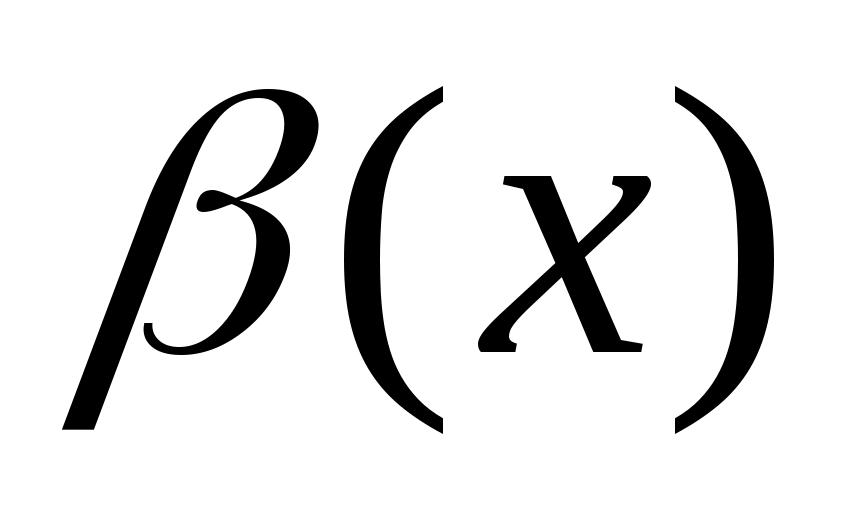 - бесконечно малые величины при - бесконечно малые величины при 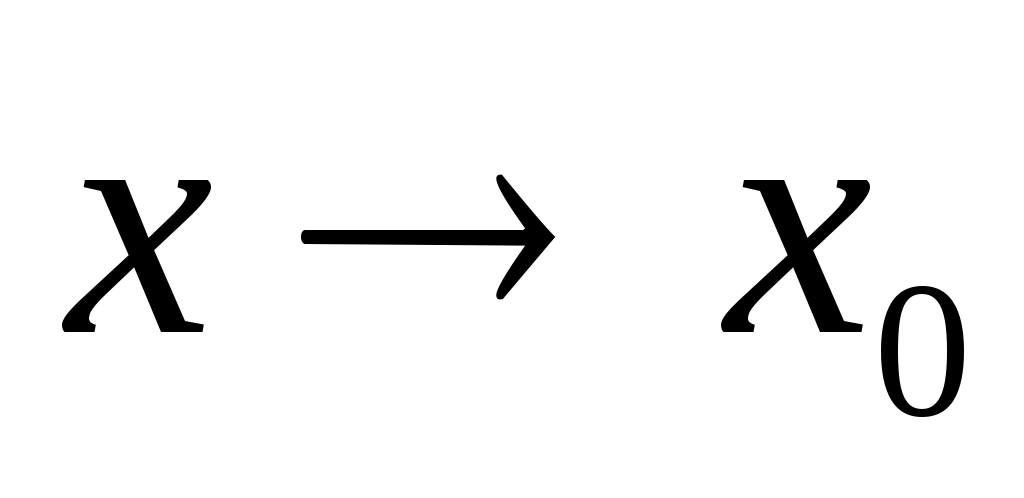 ( ( ). Перемножая почленно оба равенства, получим: ). Перемножая почленно оба равенства, получим:
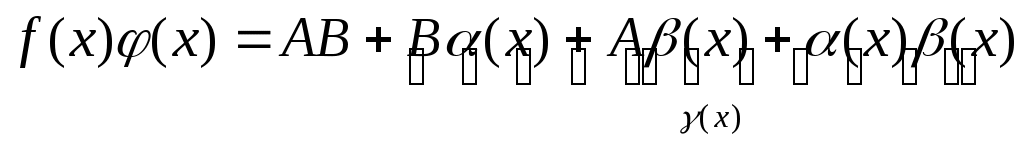 . .
На основании свойств бесконечно малых последние три слагаемые представляют величину, бесконечно малую 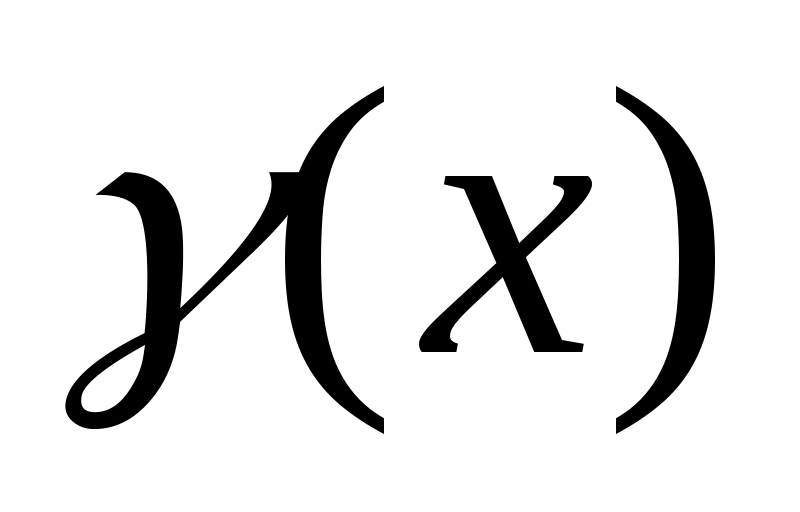 при при 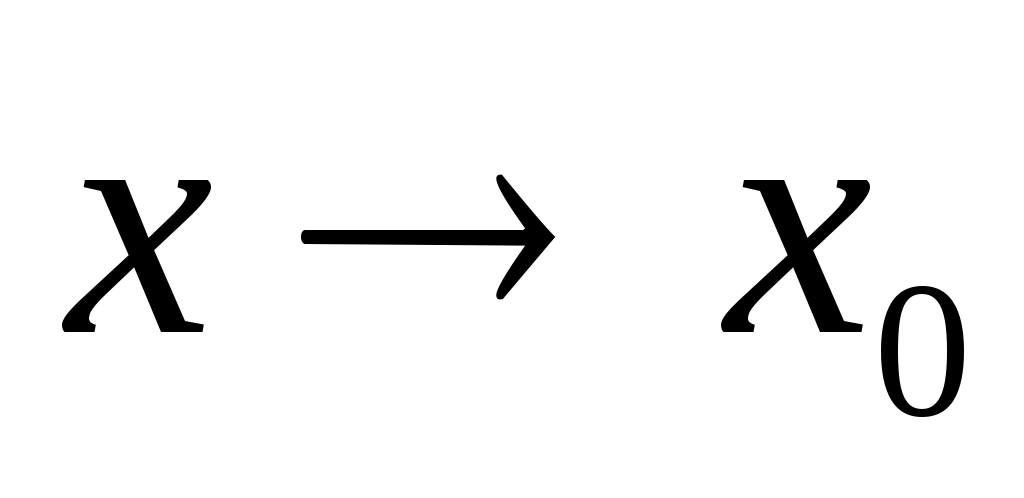 ( ( ). ).
Итак, функция 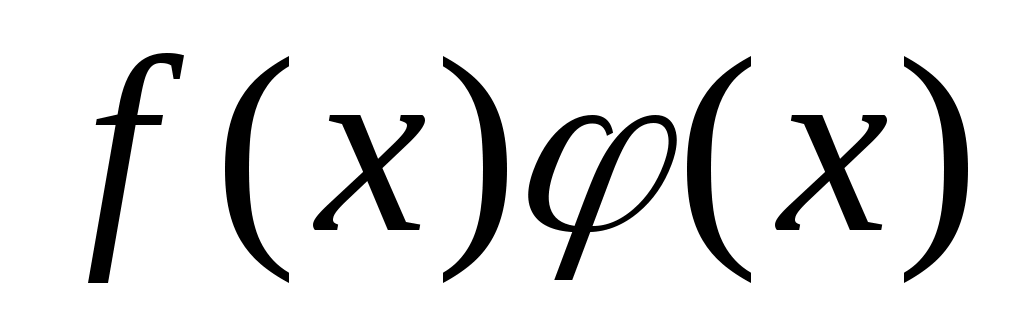 представляет сумму постоянного числа представляет сумму постоянного числа 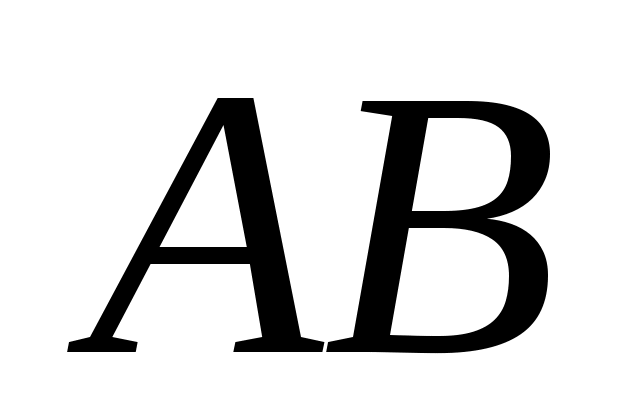 и бесконечного малой и бесконечного малой 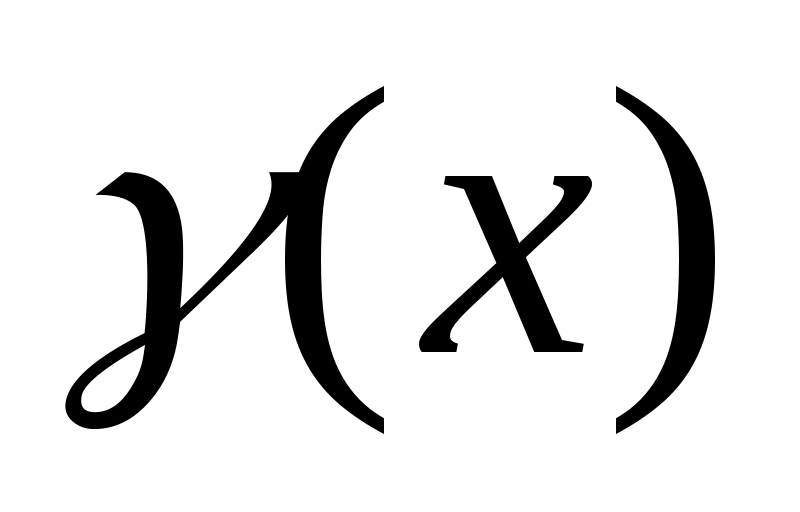 . На основании обратной теоремы о связи бесконечно малых с пределами функции это означает, что . На основании обратной теоремы о связи бесконечно малых с пределами функции это означает, что 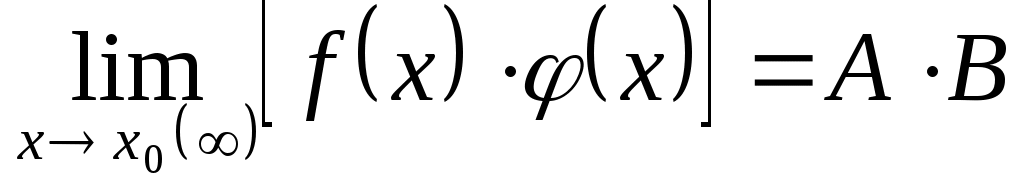 . .
В частности, постоянный множитель можно выносить за знак предела, т.е.
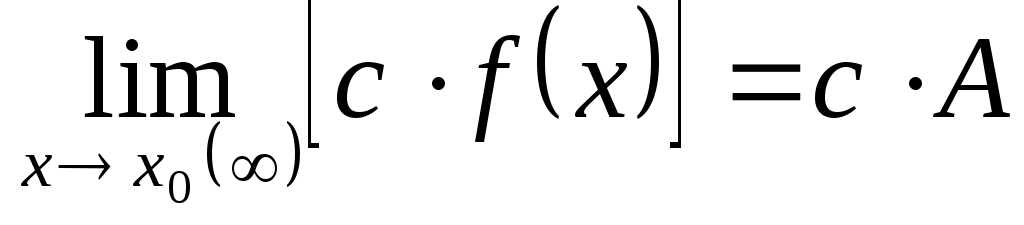 . .
|
|
|
 Скачать 2.37 Mb.
Скачать 2.37 Mb.