Ответы на экзамен по Линейной алгебре. ответы на экзамен по Линейной Алгебре. 1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами умножение на число, сложение, умножение матриц
 Скачать 2.37 Mb.
|
|
Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.е.  ,  .Если  ,  , то предел сложной функции .Если в некоторой окрестности точки  (или при достаточно больших  )  , то  .18. Бесконечно малые величины (определение). Свойства бесконечно малых (одно из них доказать). Бесконечно большие величины, их связь с бесконечно малыми. Бесконечно малые величины Определение. Функция  называется бесконечно малой величиной при  или при  , если ее предел равен нулю: .Связь бесконечно малых величин с пределами функций Теорема 1. Если функция  имеет при ( ) предел, равный  , то ее можно представить в виде суммы этого числа и бесконечно малой при ( ), т.е.  .Теорема 2. Если функцию можно представить как сумму числа и бесконечно малой при ( ), то число есть предел этой функции при ( ), т.е. .Свойства бесконечно малых величин Алгебраическая сумма конечного числа бесконечного малых величин есть величина бесконечно малая. По условию  и  - бесконечно малые величины при . Это означает, что для любого  найдутся такие числа  , что для всех  и удовлетворяющих условиям:  и  (1.1)выполняются соответствующие неравенства:  и  . (1.2)Если взять в качестве числа  минимальное из чисел  и  , т.е.  , то неравенству  будут удовлетворять решения обоих неравенств (1.1) , а, следовательно, одновременно будут верны неравенства (1.2). Складывая почленно неравенства (1.2), получим, что; .Используя свойство абсолютных величин, т.е.  , придем к более сильному неравенству: (1.3)Итак, для любого  существует такое  , что для всех  и удовлетворяющих условию верно неравенство (1.3). А это означает, что функция  есть величина бесконечно малая.Произведение бесконечно малой величины на ограниченную функцию (в т.ч. на постоянную, на другую бесконечно малую) есть величина бесконечно малая. Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая. Отношение двух бесконечно малых (неопределенность вида  ) в зависимости от характера изменения переменных в числителе и знаменателе может оказаться или числом, или бесконечно малой или бесконечностью.Бесконечно большие величины Определение. Функция  называется бесконечно большой при  , если ее предел равен бесконечности: .Свойства бесконечно больших величин Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая. Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая. Частное от деления бесконечно большой величины на функцию, имеющую предел, есть величина бесконечно большая. Об отношении или разности двух бесконечно больших функций никакого общего заключения сделать нельзя. В этих случаях говорят о неопределенностях вида  или  . В зависимости от характера изменения бесконечно больших величин их отношение или разность может оказаться или числом, или бесконечно малой, или бесконечно большой.Связь между бесконечно малыми и бесконечно большими величинами Теорема. Если функция есть бесконечно малая величина при ( ), то функция  является бесконечно большой при ( ). И, наоборот, если функция бесконечно большая при ( ), то функция есть величина бесконечно малая при ( ).19. Второй замечательный предел, число е. Понятие о натуральных логарифмах. Второй замечательный предел. Определение. Числом  (вторым замечательным пределом) называется предел числовой последовательности  : , где  Прямым вычислением можно убедиться, что  ,  (иррациональное число, число Эйлера).Если рассмотреть функцию  , то при функция имеет предел, равный числу  : .Или если  , то  .Непосредственное вычисление этого предела приводит к неопределенности  . Однако доказано, что он равен числу . Второй замечательный предел необходимо всегда использовать при раскрытии неопределенности вида .Число (число Эйлера, неперово число) играет важную роль в математическом анализе. График функции  Рассмотрим примеры вычисления пределов. Получил название экспоненты. Широко используются логарифмы по основанию , называ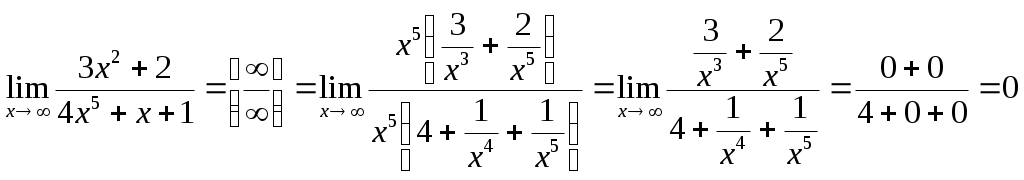емые натуральными. Натуральные логарифмы обозначаются символом  .Пример.  .Пример. 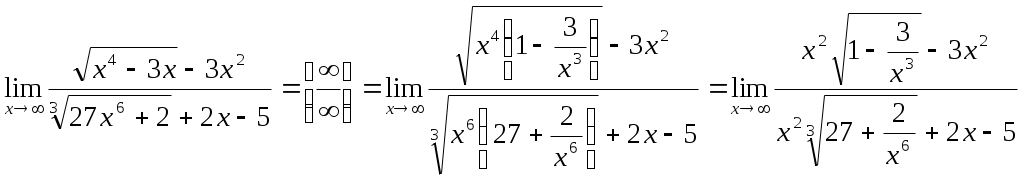 = 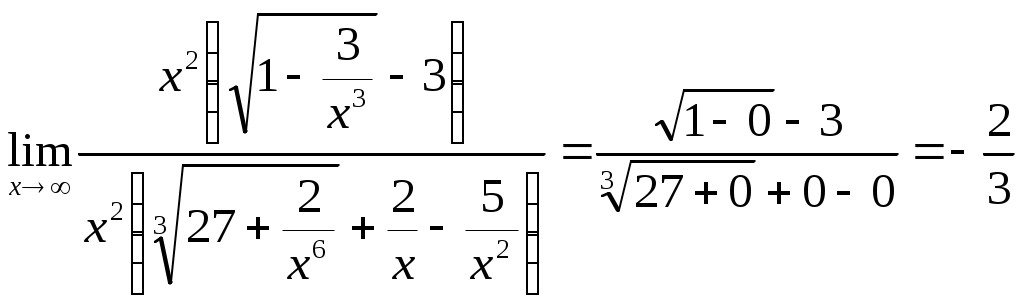.Пример.  .Пример.     .Пример.  .Пример.  .Пример. 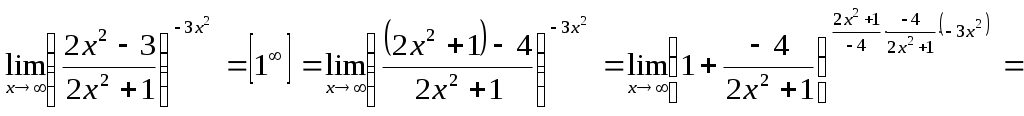 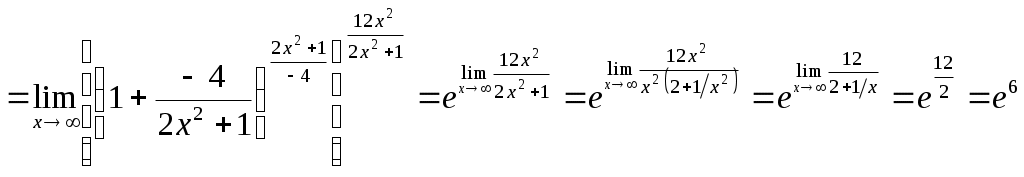 .20. Непрерывность функции в точке и на промежутке. Свойства функций, непрерывных на отрезке. Точки разрыва. Примеры. Непрерывность функции Определение 1. Функция называется непрерывной в точке  , если она удовлетворяет следующим условиям:1) определена в точке , т.е. существует  ;2) имеет конечные односторонние пределы функции при слева и справа;3) эти пределы равны значению функции в точке , т.е.  .Пример. Исследовать функции на непрерывность в точке  : а)  , б)  .Решение. а) . При  функция определена,  ,  ,  , т.е. все три условия непрерывности функции в точке выполнены. Следовательно, функция в точке непрерывна.б) . При функция не определена;  ;  . Т.о. в точке функция не является непрерывной, т.к. не выполнены первое и третье условия непрерывности функции в точке. |