Ответы на экзамен по Линейной алгебре. ответы на экзамен по Линейной Алгебре. 1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами умножение на число, сложение, умножение матриц

• Название: 1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами умножение на число, сложение, умножение матриц
• Анкор: Ответы на экзамен по Линейной алгебре
• Дата: 22.01.2023
• Размер: 2.37 Mb.
• Имя файла: ответы на экзамен по Линейной Алгебре.doc
• Тип: Решение; #898154
• страница: 10 из 10

Замечание: Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на некотором промежутке Х, то функция называется гладкой на этом промежутке. Если же производная функция допускает конечное число точек разрыва, то такая функция на данном промежутке называется кусочно гладкой.

23. Основные правила дифференцирования функций одной переменной (одно из этих правил доказать).

Производная функции м.б. найдена по схеме:

1. 
   Дадим аргументу приращение и найдем наращение значений функции .
   
2. 
   Находим приращение функции .
   
3. 
   Составляем отношение .
   
4. 
   Находим предел этого отношения при , т.е. (если этот предел существует).
   

Основные правила дифференцирования

1. 
   Производная постоянной равна нулю, т.е. .
   

□ Д о к а з а т е л ь с т в о.

При любых и имеем и . Отсюда при любом отношение и, следовательно, ■

2. 
   Производная аргумента равна единице, т.е. .
   

□ Д о к а з а т е л ь с т в о.

Рассмотрим функцию . При любых и имеем и . Отсюда при любом отношение и, следовательно, ■

3. 
   Производная алгебраической суммы конечного числа дифференцируемых функций равна алгебраической сумме производных этих функций, т.е.
   

.

4. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е.

.

□ Д о к а з а т е л ь с т в о.

Пусть и - дифференцируемые функции. Найдем производную функции по схеме:

1. 
   Дадим аргументу приращение . Тогда функции и получат наращенные значения и , а функция - значение .
   
2. 
   Найдем приращение функции: .
   
3. 
   Составим отношение , которое представим в виде: .
   
4. 
   Найдем предел этого отношения при , используя теоремы о пределах:
   

На основании определения производной получили, что:

или . ■

Следствие 1. Постоянный множитель можно выносить за знак производной:

.

Следствие 2.Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные, например:

.

5. Производная частного двух дифференцируемых функций может быть найдена по формуле

(при условии, что ).

□ Д о к а з а т е л ь с т в о.

1) Дадим аргументу х приращение . Тогда функции и получат наращенные значения и , а функция - значение .

2) Найдем приращение функции:

3) Составим отношение 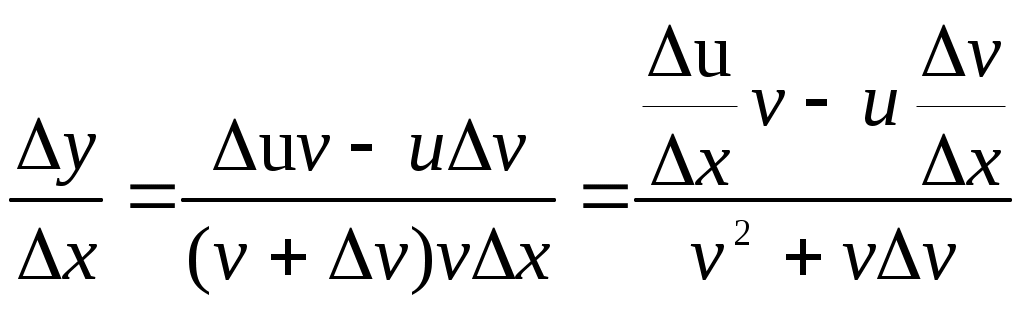, которое представим в виде:

4) Найдем предел этого отношения при , используя теоремы о пределах: ■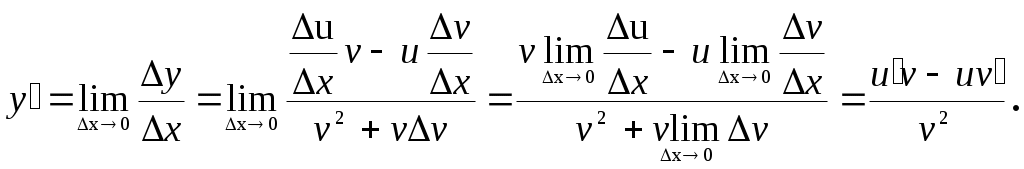

24. Формулы производных основных элементарных функций (одну из формул вывести). Производная сложной функции.

Производные основных элементарных функций (таблица производных)

1. 
   Производная логарифмической функции.
   

А) . Воспользуемся схемой нахождения производных:

1) Дадим аргументу приращение и найдем наращение значений функции .

2) Находим приращение функции .

3) Составляем отношение .

4) Находим предел этого отношения при , т.е. .

Обозначив , найдем и .

В силу непрерывности логарифмической функции, используя 3 свойство функций непрерывных в точке. (Если функция 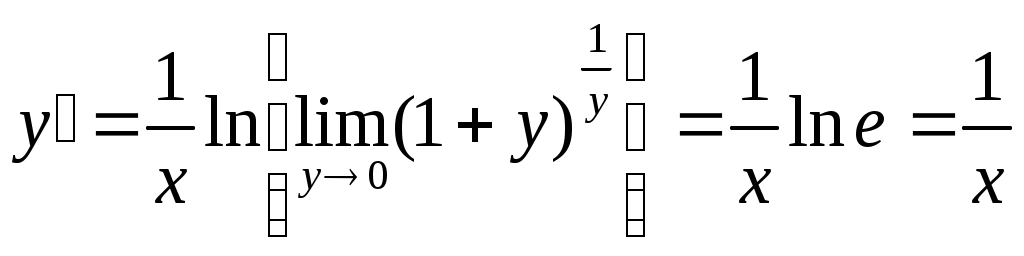непрерывна в точке , а функция непрерывна в точке , то сложная функция непрерывна в точке - ), меняем местами символы предела и логарифма, а затем используем определение числа ; получим:

.

Итак, и .

Б) . Найдем , т.е.

и .

2. 
   Производная показательной функции.
   

А) - прологарифмируем обе части равенства по основанию : . Дифференцируем или , откуда , т.е.

и .

Б) . . Итак,

и

3. 
   Производная степенной функции.
   

, для любого . Прологарифмируем обе части равенства . Дифференцируем: , откуда , т.е:

и

4. 
   Производная степенно-показательной функции.
   

. . Дифференцируем: .

5. 
   Производная тригонометрических функций.
   

и

и

и

и

Производная сложной функции

Пусть задана сложная функция .

Теорема. Если и - дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженной на производную промежуточного аргумента по независимой переменной , т.е.

.

□ Дадим независимой переменной х приращение Δх≠0. Тогда функция u= φ(x) и у=f(u) соответственно получат приращения Δu и Δy.

Предположим, что Δu≠0. Тогда в силу дифференцируемости функции у=f(u) можно записать где - f′(u) величина не зависящая от Δu.

На основании теоремы о связи бесконечно малых величин с пределами функций где - бесконечно малая величина при Δu → 0, откуда

Это равенство будет справедливо и при Δu = 0, если полагать, что α(∆u=0)=0 (т.е. доопределить таким образом функцию α(∆u) при ∆u=0).

Разделив обе части последнего равенства на Δх≠0, получим

Так как по условию функция у=φ(х) дифференцируема, то она непрерывна в точке х, следовательно, при Δх → 0 Δu → 0 и α(∆u) → 0 .

Поэтому, переходя к пределу при Δх → 0 в последнем соотношении, получаем ■

25. Теоремы Ролля и Лагранжа (без доказательства). Геометрическая интерпретация этих теорем.

Теорема Ролля. Пусть функция удовлетворяет следующим условиям:

1. 
   непрерывна на отрезке ;
   
2. 
   дифференцируема на интервале ;
   
3. 
   на концах отрезка принимает разные значения, т.е. .
   

Т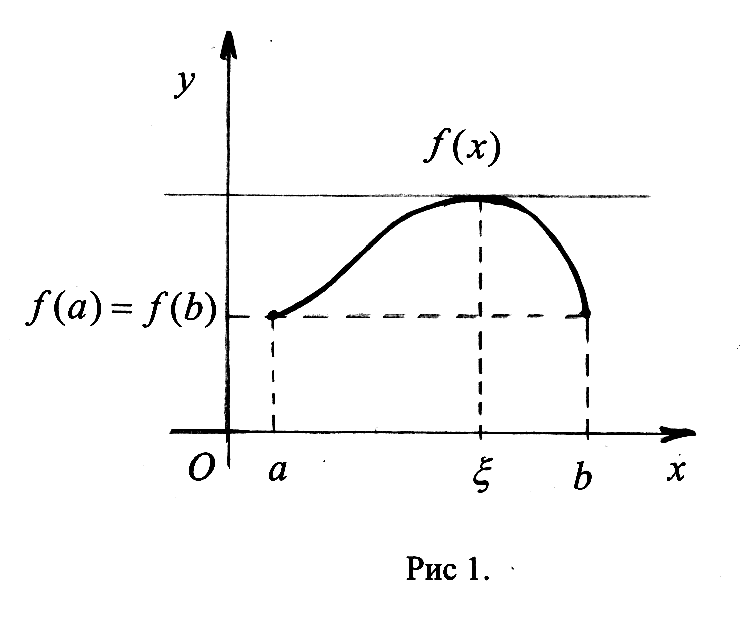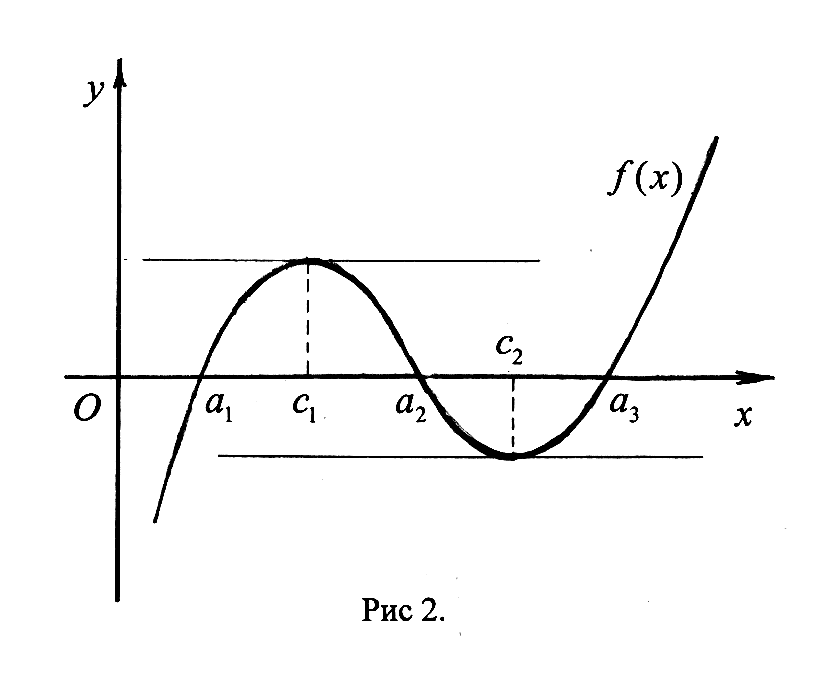



огда внутри отрезка существует по крайней мере одна точка , в которой производная функции равна нулю: .

Геометрический смысл теоремы Ролля. При выполнении условий теоремы внутри отрезка найдется точка , в которой касательная, проведенная к графику функции , параллельна оси (см. рис. 1). Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки.

Замечание. Пусть . Тогда и – нули функции , и между ними найдется такая точка , что . Таким образом, из теоремы Ролля следует, что между нулями дифференцируемой функции находится хотя бы один нуль производной (см. рис. 2).

Теорема Роля является частным случаем теоремы Лагранджа.

Теорема Лагранжа. Пусть функция удовлетворяет следующим условиям:

1. 
   непрерывна на отрезке ;
   
2. 
   дифференцируема на интервале .
   

Тогда внутри отрезка существует по крайней мере одна точка , в которой выполняется равенство: .

Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке.

Н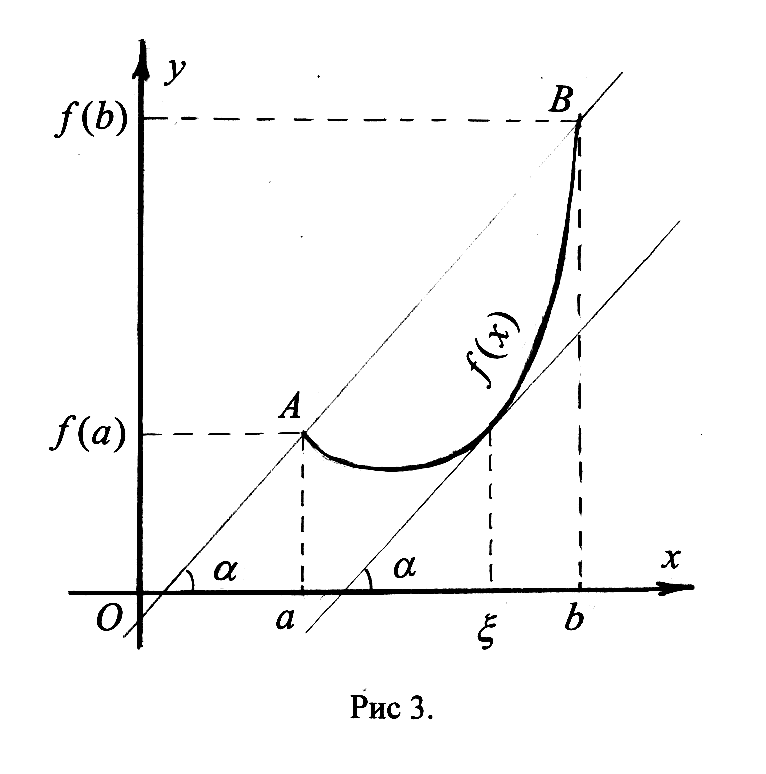

а рис (см. рис. 3) хорда AB – отрезок, соединяющий точки и . Величина равна тангенсу угла наклона прямой AB.

Геометрический смысл теоремы Лагранжа заключается в том, что при выполнении условий теоремы внутри отрезка найдется точка , в которой касательная, проведенная к графику функции , параллельна хорде AB. Таких точек может быть и несколько, но одна существует точно.

Следствие. При выполнении условий теоремы Лагранжа .

Эту формулу называют формулой конечных приращений.