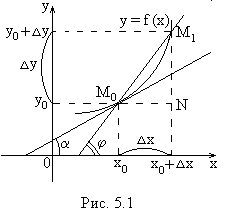Ответы на экзамен по Линейной алгебре. ответы на экзамен по Линейной Алгебре. 1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами умножение на число, сложение, умножение матриц
 Скачать 2.37 Mb.
|
|
Определение 2. Функция  называется непрерывной в точке  , если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:  .Определения 1 и 2 равносильны. Точка называется точкой разрыва функции  , если эта функция в данной точке не является непрерывной. Различают точки разрыва:Первого рода – когда существуют конечные односторонние пределы функции слева и справа при  , не равные друг другу. К точкам разрыва первого рода относятся также точки устранимого разрыва, когда предел функции при существует, но не равен значению функции в этой точке.Второго рода – когда хотя бы один из односторонних пределов слева или справа равен бесконечности или не существует. Свойства функций, непрерывных в точке 1. Если функции и  непрерывны в точке , то их сумма  , произведение  и частное  (при условии  ) являются функциями, непрерывными в точке .2. Если функция непрерывна в точке и  , то существует такая окрестность точки , в которой  .Доказательство этого свойства основывается на том, что при малых приращениях аргумента  можно получить как угодно малое приращение функции  в окрестностях  не изменится.3. Если функция  непрерывна в точке  , а функция  непрерывна в точке , то сложная функция непрерывна в точке . Доказательство состоит в том, что малому приращению аргумента соответствует как угодно малое приращение  , приводящее в свою очередь к непрерывности функции к как угодномалому приращению  .Свойство можно записать:  ,Т.е. под знаком непрерывной функции можно переходить к пределу. Определение. Функция называется непрерывной на промежутке  , если она непрерывна в каждой точке этого промежутка. Все элементарные функции непрерывны в области их определения.Точки разрыва функции Определение. Если в какой-нибудь точке для функции не выполняется по крайней мере одно из условий непрерывности, то эта точка называется точкой разрыва функции.Причем: 1) Если существуют конечные односторонние пределы функции, неравные друг другу:  , то точка - точка разрыва I рода.2) Если хотя бы один из односторонних пределов функции  или  равен бесконечности или не существует, то точка - точка разрыва II рода.Свойства функций, непрерывных на отрезке 1. Если функция непрерывна на отрезке  , то она ограничена на этом отрезке. (рис. 1.1)2. Если функция непрерывна на отрезке , то она достигает на этом отрезке наименьшего значения  и наибольшего значения (теорема Вейерштрасса). (рис. 1.2)3  . Если функция непрерывна на отрезке и значения ее на концах отрезка  и  имеют противоположные знаки, то внутри отрезка найдется точка  такая, что  . (Теорема Больцано-Коши.)П  ример. Исследовать на непрерывность и найти точки разрыва функции  . Установить характер разрыва.Решение. При  функция не определена, следовательно, функция в точке терпит разрыв:  , а  . Так как односторонние пределы бесконечны, то - точка разрыва второго рода.21. Производная и ее геометрический смысл. Уравнение касательной к плоской кривой в заданной точке. Определение производной Пусть на некотором промежутке Х определена функция y=f(x). Возьмем любую точку  . Зададим аргументу х произвольное приращение ∆х ≠ 0 такое, что точка х+∆х также будет принадлежать Х. Функция получит приращение ∆у=f(x+∆х)−f(x).Определение. Производной функции y=f(x) в точке х называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (при условии, что этот предел существует). Для обозначения производной функцииy=f(x) в точке х используются символы у′(х) или f′(x). Итак, по определению,  .Если для некоторого значения х0 выполняется условие  или  ,т.е. пределы равны бесконечности, то говорят, что в точке х0 функция имеет бесконечную производную. Если функция y=f(x)имеет конечную производную в каждой точке , то производную f′(x) можно рассматривать как функцию х, также определенную на Х. Нахождение производной функции называется дифференцированием функции. Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках промежутка Х, называется дифференцируемой на этом промежутке.Задача о касательной Пусть на плоскости  дана непрерывная функция и необходимо найти уравнение касательной к этой кривой в точке  .
Из задачи о касательной следует геометрический смысл производной: производная f′(x0) есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой у=f′(x) в точке х0, т.е. k= f′(x0). Следовательно, уравнение касательной к кривой y=f(x) в точке х0 примет вид  Пример. Найти производную функции f(x)=х2. Решение. Придавая аргументу х приращение ∆х, найдем соответствующее приращение функции:  Составим отношение:  Найдем предел этого отношения при ∆х → 0:  22. Дифференцируемость функций одной переменной. Связь между дифференцируемостью и непрерывностью функции (доказать теорему). Понятие дифференцируемости функции Определение. Функция y=f(x) называется дифференцируемой в точке х, если ее приращение Δу в этой точке можно представить в виде  ,где А – некоторое число, не зависящее от  , а α( ) – функция аргумента , являющаяся бесконечно малой при →0, т.е.  Выясним теперь связь между дифференцируемостью в точке и существованием производной в той же точке. Теорема. Для того чтобы функция f(x) была дифференцируемой в данной точке х , необходимо и достаточно, чтобы она имела в этой точке конечную производную. Связь между дифференцируемостью функции и ее непрерывностью Пример. Доказать, что функция y=│х│ недифференцируема в точке х=0 . Решение. Производная функции (если она существует) равна  Очевидно, что при х=0 производная не существует, так как отношение  , т.е. не имеет предела при Δх→0 (ни конечного, ни бесконечного). Геометрически это означает отсутствие касательной к кривой в точке х=0.Теорема. Если функция y=f(x) дифференцируема в точке х0,, то она в этой точке непрерывна. □Доказательство. По условия функция y=f(x) дифференцируема в точке х0, т.е. существует конечный предел  где f′(x0) – постоянная величина, не зависящая от .Тогда на основании теоремы о связи бесконечно малых величин с пределами функций можно записать  где α(∆х) является бесконечно малой величиной при →0, или  .При Δх→0 на основании свойств бесконечно малых величин устанавливаем, что Δу→0 и, следовательно, по определению непрерывности функции в точке, делаем вывод, что функция непрерывна в токе х0. ■ Обратная теорема, вообще говоря, неверна, если функция непрерывна в данной точке, то она не обязательно дифференцируема в этой точке. Так, функция y=│х│ непрерывна в точке х0=0, ибо  но, как было доказано ранее недифференцируема в этой точке.Таким образом, непрерывность функции – необходимое, но не достаточное условие ее дифференцируемости. |
, принадлежащей этой прямой, и угловому коэффициенту имеет вид: 
,
, (
- угол наклона прямой).
(рис.5.1) найдем тангенс угла наклона секущей 
: 
. 
приближать к точке 
, то угол 
будет стремиться к углу 
. 
.