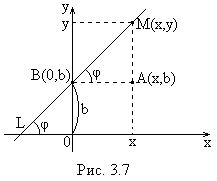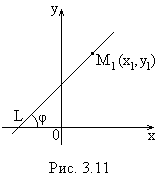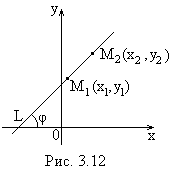Ответы на экзамен по Линейной алгебре. ответы на экзамен по Линейной Алгебре. 1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами умножение на число, сложение, умножение матриц

• Название: 1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами умножение на число, сложение, умножение матриц
• Анкор: Ответы на экзамен по Линейной алгебре
• Дата: 22.01.2023
• Размер: 2.37 Mb.
• Имя файла: ответы на экзамен по Линейной Алгебре.doc
• Тип: Решение; #898154
• страница: 6 из 10

Взаимное расположение двух линий

Чтобы определить взаимное расположение 2-х линий, необходимо знать уравнений этих линий. Если система этих уравнений совместна, то линии имеют общие точки. В противном случае общих точек нет. Число общих точек равно числу решений системы уравнений

Например, прямая линия и окружность 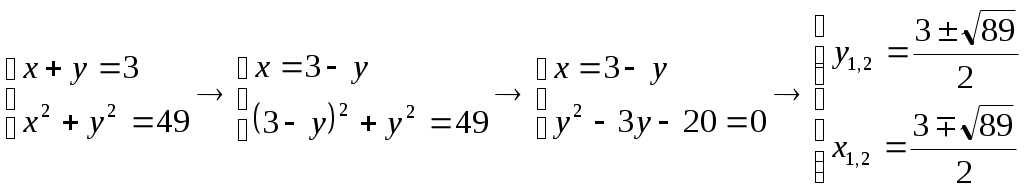имеют 2 общие точки, так как система из этих уравнений имеет два решения:

.

Уравнение прямой на плоскости

В декартовой системе координат рассмотрим прямую , расположенную под углом к оси (рис. 3.7).

Выберем на прямой L произвольную точку . Из найдем тангенс угла наклона прямой: . Введем угловой коэффициент прямой . Из последнего равенства (3.1)

Полученное уравнение называется уравнением прямой с угловым коэффициентом.

Частные случаи уравнения (3.1):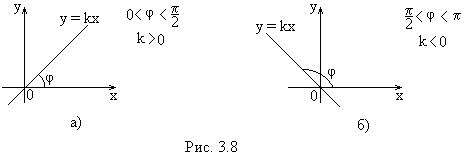

1. 
   Если , тогда и уравнение (3.1) представляет прямую, проходящую через начало координат под углом к оси (рис. 3.8).
   

2. 
   Если (т.е. ), тогда и уравнение (3.1) представляет собой прямую, параллельную оси (рис. 3.9).
   

3. 
   Если , тогда прямая (рис. 3.10). Предположим, что отсекает на оси отрезок, равный (рис. 3.10). Очевидно, что уравнений такой прямой .
   

Уравнение прямой, проходящей через заданную точку в данном направлении

Пусть прямая образует с осью угол и проходит через точку . Т.к. , то ее координаты удовлетворяют уравнению (3.1), т.е. . (3.2) Вычитая из (3.1) уравнение (3.2), получим . (3.3) Полученное уравнение называется уравнением прямой по точке и угловому коэффициенту .

Уравнение прямой, проходящей через две заданные точки

Пусть известны две точки, принадлежащие , . Запишем уравнение прямой по точке и угловому коэффициенту : . (3.4) Т.к. точка также принадлежит , то ее координаты будут удовлетворять данное равенство: .

Из последнего равенства . Подставляя выражение для в уравнение (3.4): , получим уравнение прямой по двум точкам

(3.5).

Уравнение пучка прямых



Уравнение прямой в отрезках



Уравнение называется уравнением прямой в отрезках.

Общее уравнение прямой и его исследование

Рассмотрим уравнение прямой с угловым коэффициентом . Перенесем все слагаемые в левую часть и перепишем его в следующем виде:

,

- (3.6)

общее уравнение прямой, где и не равны нулю одновременно, т.е. .

Рассмотрим частные случаи уравнения (3.6).

1. 
   Если , т.е. уравнение (3.6) не содержит , то оно представляет прямую, параллельную оси (рис. 3.9):
   

.

Если - уравнение оси .

2. 
   Если (уравнение не содержит ), тогда прямая параллельна оси (рис.3.10):
   

.

Если - уравнение оси .

3) Если , тогда уравнение имеет вид и прямая проходит через начало координат (рис. 3.8).

Точка пересечения прямых

Если заданы две прямые 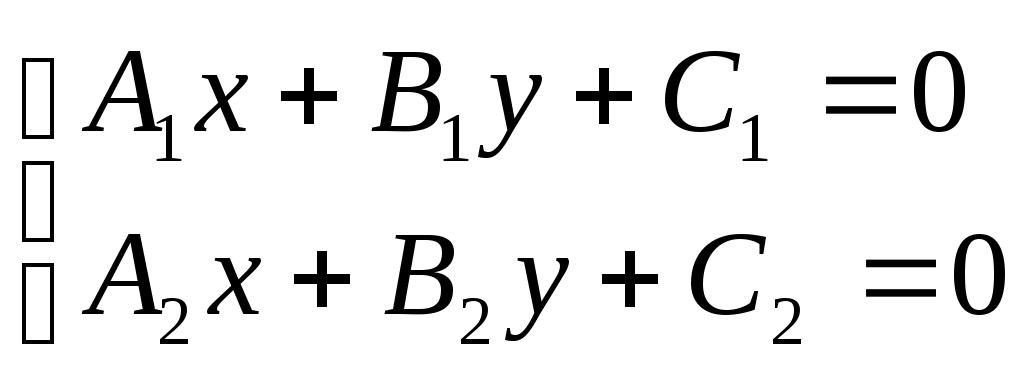и , то координаты точки их пересечения должны удовлетворять уравнению каждой прямой, т.е. они могут быть найдены из системы: .

Если прямые не параллельны, т.е. , то решение системы дает единственную точку пересечения прямых.

15. Общее уравнение прямой на плоскости, его исследование. Условия параллельности и перпендикулярности прямых.

Общее уравнение прямой и его исследование

Рассмотрим уравнение прямой с угловым коэффициентом . Перенесем все слагаемые в левую часть и перепишем его в следующем виде:

,

- (3.6)

общее уравнение прямой, где и не равны нулю одновременно, т.е. .

Рассмотрим частные случаи уравнения (3.6).

1. 
   Пусть . Тогда уравнение можно записать в виде: . Обозначим .
   

Если , , то получим (уравнение прямой с угловым коэффициентом);

Если , , то (уравнение прямой, проходящей через начало координат);

Если , , то (уравнение прямой, параллельной оси Оу);

Если , , то (уравнение оси Ох).

3. 
   Пусть , . Тогда уравнение примет вид . Обозначим .
   

Если , то получим (уравнение прямой, параллельной оси Оу);

Если , то (уравнение оси Оу).

Т.о., при любых значениях коэффициентов , (не равных одновременно нулю) и уравнение есть уравнение некоторой прямой линии на плоскости Оху.

- общее уравнение прямой.

Условия параллельности и перпендикулярности двух прямых:

Если прямые и параллельны, то угол и , откуда из формулы угла между двумя прямыми . И наоборот, если , то по этой же формуле и .

Т.о., равенство угловых коэффициентов является необходимым и достаточным условием параллельности 2х прямых.

- условие параллельности двух прямых.

Если прямые перпендикулярны, то , при этом или , откуда или .

Справедливо так же и обратное утверждение.

Т.о., для перпендикулярности прямых необходимо и достаточно, чтобы их угловые коэффициенты были обратны по величине и противоположны по знаку.

- условие перпендикулярности двух прямых.

Если две прямые заданы уравнениями в общем виде: и ,то учитывая их угловые коэффициенты и , условие параллельности прямых имеет вид: .

Следовательно, условием параллельности прямых, заданных общими уравнениями является пропорциональность коэффициентов при переменных.

Условие перпендикулярности прямых в этом случае примет вид или ,

Т.е. условием перпендикулярности двух прямых, заданных общими уравнениями, является равенство нулю суммы произведений коэффициентов при переменных х и у.

16. Предел последовательности при и предел функции при . Признаки существования предела (с доказательством теоремы о пределе промежуточной функции).

Предел числовой последовательности

Определение. Если по некоторому закону каждому натуральному числу поставлено в соответствие вполне определенное число , то говорят, что задана числовая последовательность :

.

Другими словами, числовая последовательность - это функция натурального аргумента: .

Числа называются членами последовательности, а число - общим или -м членом данной последовательности.

Примеры числовых последовательностей:

1) (монотонная, неограниченная),

2) (не монотонная, ограниченная)

3)

Рассмотрим числовую последовательность 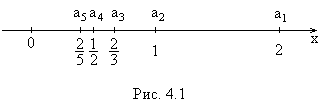, изобразив ее точками на числовой оси (рис.4.1):



Видно, что члены последовательности с ростом как угодно близко приближаются к 0. При этом абсолютная величина разности становится все меньше и меньше.