1. составление разбивочной схемы сборного перекрытия
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
|
3.4. Расчет по прочности ригеля при действии поперечных сил Для расчета прочности по сечениям, наклонным к продольной оси, принимают значения поперечных сил ригеля, большие из двух расчетов: упругого расчета и с учетом перераспределения моментов [6]. Для всех вариантов загружения максимальные значения поперечных сил: − 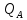 = 313,77 кН от загружения I (1+2), = 313,77 кН от загружения I (1+2),− 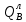 = -481,49 кН от загружения II (1+3), = -481,49 кН от загружения II (1+3),− 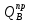 = 456,72 кН от загружения II (1+3), = 456,72 кН от загружения II (1+3),− 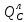 = -424,24 кН от загружения III (1+4). = -424,24 кН от загружения III (1+4).Величина максимальных поперечных сил у грани стены при длине площадки опирания ригеля на стену aоп = 380 мм и у граней колонн при высоте их сечения hc = 400 мм 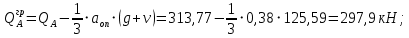 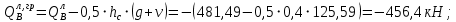 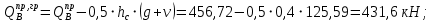 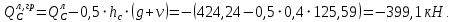 Проверяем условие: Qmin > 0,5γb1·Rbt·b·h0, где Qmin – минимальное значение поперечной силы на опорах; 0,5γb1·Rbt·b·h0 соответствует образованию наклонной трещины. Если условие выполняется, то поперечную арматуру устанавливаем по расчету, иначе осуществляется конструктивное армирование. Для расчетов по прочности при действии поперечных сил принимаем рабочую высоту сечения от верхней грани ригеля до центра тяжести продольной рабочей арматуры, расположенной в нижней зоне h0 = 530 мм. Минимальное значение поперечной силы на опорах Qmin = 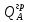 = 297,9 кН. = 297,9 кН.0,5γb1·Rbt·b·h0 = 0,5 · 0,9 ·1,05·103 · 0,3 · 0,53 = 75,1 кН, 297,9 кН > 75,1 кН, следовательно, поперечная арматура в ригеле должна устанавливаться по расчету. Принимаем поперечную арматуру класса A500С с Rsw = 300 МПа. Согласно п. 10.3.12 [3] диаметр поперечной арматуры в сварном каркасе подбирается из условия технологии сварки с наибольшим диаметром продольной арматуры. В трех плоских сварных каркасах каждого пролета ригеля при наибольшем диаметре стержней продольной рабочей арматуры 28 мм поперечные стержни из условия технологии сварки принимаем диаметром 8 мм (dw ≥ 0,25·d). 3.4.1. Расчет по прочности ригеля при действии поперечных сил у опор В и С Поперечные силы у опор В и С соответственно равны 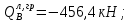 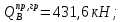 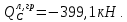 Расчеты ригеля по полосе между наклонными сечениями и по наклонным сечениям на действие поперечных сил выполняем для опоры с максимальным значением поперечной силы Qmax = Расчеты ригеля по полосе между наклонными сечениями и по наклонным сечениям на действие поперечных сил выполняем для опоры с максимальным значением поперечной силы Qmax = 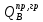 = 431,6 кН. = 431,6 кН.Максимально допустимый шаг стержней поперечной арматуры у опор В и С в соответствии с п. 10.3.13 [3]: sw ≤ 0,5h0 = 0,5·530 = 265 мм; sw ≤ 300 мм. В соответствии с п. 3.2.22 [7] шаг поперечной арматуры, учитываемой в расчете, должен быть не более: 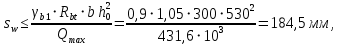 где Qmax = 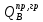 = 431,6 кН. = 431,6 кН.В расчет принимаем наименьшее значение шага поперечной арматуры с округлением в меньшую сторону кратно 50 мм. В первом приближении принимаем поперечную арматуру dw = 8 мм класса А500C, с площадью поперечного сечения трех стержней Asw = 151 мм2 с шагом sw = 150 мм. Расчет ригеля по полосе между наклонными сечениями Q ≤ φb1·γb1·Rb·b·h0, где φb1 – коэффициент, принимаемый равным 0,3; Q – поперечная сила в нормальном сечении, принимаемом на расстоянии от опоры не менее h0. Q = 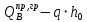 = 431,6 – 125,4 = 431,6 – 125,4  0,53 = 365,2 кН. 0,53 = 365,2 кН.φb1·γb1·Rb·b·h0 = 0,3  0,9 0,9  14,5 14,5  103 103  0,3 0,3  0,53 = 622,5 кН, 0,53 = 622,5 кН,365,2 кН < 622,5 кН, условие выполняется, следовательно, прочность наклонной полосы на сжатие обеспечена. Расчет ригеля по наклонным сечениям на действие поперечных сил Определяем усилие в поперечной арматуре на единицу длины элемента: 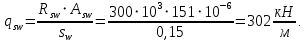 Поперечную арматуру учитывают в расчете, если соблюдается условие: qsw ≥ 0,25·γb1·Rbt·b, 0,25γb1·Rbt·b = 0,25·0,9·1,05·103·0,3 = 70,9 кН/м, 302 кН/м > 70,9 кН/м, условие выполняется, следовательно, поперечная арматура учитывается в расчете. Момент воспринимаемый бетоном при действии поперечной силы: 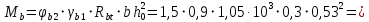 119,5 кН 119,5 кН  м, м,где φb2 – коэффициент, принимаемый равным 1,5. Определяем длину проекции невыгоднейшего наклонного сечения: 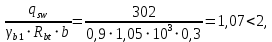 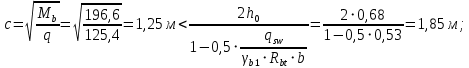 тогда 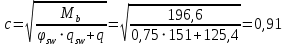 м, но не менее h0 и не более 3h0. м, но не менее h0 и не более 3h0.h0 = 0,53 м ≤ с ≤ 3h0 = 3·0,53 = 1,59 м. Принимаем c = 0,91 м. Длину проекции наклонной трещины c0 принимают равным c, но не менее h0 и не более 2h0. h0 = 0,53 м ≤ с ≤ 2h0 = 2·0,53 = 1,06 м. Принимаем c = c0 = 0,91 м. Поперечная сила, воспринимаемая поперечной арматурой: Qsw = φsw·qsw·c0 = 0,75·302·0,91 = 206,1 кН. Поперечная сила, воспринимаемая бетоном: 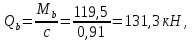 но не более Qb,max = 2,5γb1·Rbt·b·h0 = 2,5·0,9·1,05·103·0,3·0,53 = 375,6 кН, и не менее Qb,min = 0,5γb1·Rbt·b·h0 = 0,5·0,9·1,05·103·0,3·0,53 = 75,1 кН. Принимаем Qb = 131,3 кН. Определяем поперечную силу Q с учетом возможности отсутствия временной нагрузки на приопорном участке длиной с Q = 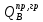 − v·c = 431,6 − 92,98· 0,91 = 346,99 кН. − v·c = 431,6 − 92,98· 0,91 = 346,99 кН.Проверяем условие Q = 346,99 кН > Qb + Qsw = 131,3 + 206,1 = 337,4 кН, то есть прочность по наклонным сечениям на действие поперечных сил у опор В и С не обеспечена. Увеличиваем диаметр арматуры dw = 10 мм класса А500C, с площадью поперечного сечения трех стержней Asw = 236 мм2 с шагом sw = 150 мм. 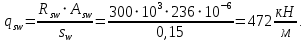 Поперечную арматуру учитывают в расчете, если соблюдается условие: qsw ≥ 0,25·γb1·Rbt·b, 0,25γb1·Rbt·b = 0,25·0,9·1,05·103·0,3 = 70,9 кН/м, 472 кН/м > 70,9 кН/м, условие выполняется, следовательно, поперечная арматура учитывается в расчете. Момент воспринимаемый бетоном при действии поперечной силы: 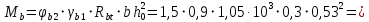 119,5 кН 119,5 кН  м, м,где φb2 – коэффициент, принимаемый равным 1,5. Определяем длину проекции невыгоднейшего наклонного сечения: 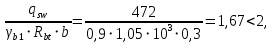 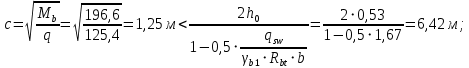 тогда 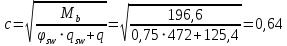 м, но не менее h0 и не более 3h0. м, но не менее h0 и не более 3h0.h0 = 0,53 м ≤ с ≤ 3h0 = 3·0,53 = 1,59 м. Принимаем c = 0,64 м. Длину проекции наклонной трещины c0 принимают равным c, но не менее h0 и не более 2h0. h0 = 0,53 м ≤ с ≤ 2h0 = 2·0,53 = 1,06 м. Принимаем c = c0 = 0,64 м. Поперечная сила, воспринимаемая поперечной арматурой: Qsw = φsw·qsw·c0 = 0,75·472·0,81 = 286,7 кН. Поперечная сила, воспринимаемая бетоном: 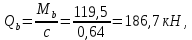 но не более Qb,max = 2,5γb1·Rbt·b·h0 = 2,5·0,9·1,05·103·0,3·0,53 = 375,6 кН, и не менее Qb,min = 0,5γb1·Rbt·b·h0 = 0,5·0,9·1,05·103·0,3·0,53 = 75,1 кН. Принимаем Qb = 186,7 кН. Определяем поперечную силу Q с учетом возможности отсутствия временной нагрузки на приопорном участке длиной с Q = 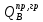 − v·c = 431,6 − 92,98· 0,64 = 372,1 кН. − v·c = 431,6 − 92,98· 0,64 = 372,1 кН.Проверяем условие Q = 372,1 кН < Qb + Qsw = 186,7 + 286,7 = 473,4 кН, то есть прочность по наклонным сечениям на действие поперечных сил у опор В и С обеспечена. На средних опорах В и С концы стержней нижней арматуры неразрезного ригеля приварены к закладным деталям, что обеспечивает анкеровку продольной арматуры, поэтому расчет ригеля по наклонным сечениям на действие моментов не производим. 3.4.2. Расчет по прочности ригеля при действии поперечных сил у опоры А Максимально допустимый шаг стержней поперечной арматуры у опоры А в соответствии с п. 10.3.13 [3]: sw ≤ 0,5h0 = 0,5·530 = 265 мм; sw ≤ 300 мм. В соответствии с п. 3.2.22 [7] шаг поперечной арматуры, учитываемой в расчете, должен быть не более: 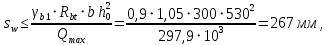 где Qmax = 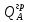 = 297,9 кН. = 297,9 кН.В расчет принимаем наименьшее значение шага поперечной арматуры с округлением в меньшую сторону кратно 50 мм. В первом приближении принимаем поперечную арматуру dw = 10 мм класса А500C, с площадью поперечного сечения трех стержней Asw = 236 мм2 с шагом sw = 250 мм. Расчет ригеля по полосе между наклонными сечениями Q ≤ φb1·γb1·Rb·b·h0, где φb1 – коэффициент, принимаемый равным 0,3; Q – поперечная сила в нормальном сечении, принимаемом на расстоянии от опоры не менее h0. Q = 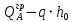 = 297,9 – 125,4 = 297,9 – 125,4  0,53 = 231,4 кН. 0,53 = 231,4 кН.φb1·γb1·Rb·b·h0 = 0,3  0,9 0,9  14,5 14,5  103 103  0,3 0,3  0,53 = 622,5 кН, 0,53 = 622,5 кН,231,4 кН < 622,5 кН, условие выполняется, следовательно, прочность наклонной полосы на сжатие обеспечена. Расчет ригеля по наклонным сечениям на действие поперечных сил Определяем усилие в поперечной арматуре на единицу длины элемента: 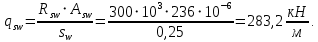 Поперечную арматуру учитывают в расчете, если соблюдается условие: qsw ≥ 0,25·γb1·Rbt·b, 0,25γb1·Rbt·b = 0,25·0,9·1,05·103·0,3 = 70,9 кН/м, 283,2 кН/м > 70,9 кН/м, условие выполняется, следовательно, поперечная арматура учитывается в расчете. Момент воспринимаемый бетоном при действии поперечной силы: 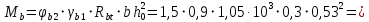 119,5 кН 119,5 кН  м, м,где φb2 – коэффициент, принимаемый равным 1,5. Определяем длину проекции невыгоднейшего наклонного сечения: 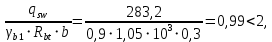 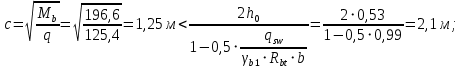 тогда 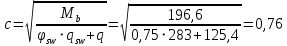 м, но не менее h0 и не более 3h0. м, но не менее h0 и не более 3h0.h0 = 0,53 м ≤ с ≤ 3h0 = 3·0,53 = 1,59 м. Принимаем c = 0,99 м. Длину проекции наклонной трещины c0 принимают равным c, но не менее h0 и не более 2h0. h0 = 0,53 м ≤ с ≤ 2h0 = 2·0,53 = 1,06 м. Принимаем c = c0 = 0,99 м. Поперечная сила, воспринимаемая поперечной арматурой: Qsw = φsw·qsw·c0 = 0,75·283,2·0,99 = 210,1 кН. Поперечная сила, воспринимаемая бетоном: 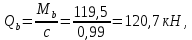 но не более Qb,max = 2,5γb1·Rbt·b·h0 = 2,5·0,9·1,05·103·0,3·0,53 = 375,6 кН, и не менее Qb,min = 0,5γb1·Rbt·b·h0 = 0,5·0,9·1,05·103·0,3·0,53 = 75,1 кН. Принимаем Qb = 120,7 кН. Определяем поперечную силу Q с учетом возможности отсутствия временной нагрузки на приопорном участке длиной с Q = 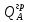 − v·c = 297,9 − 92,98· 0,99 = 205,9 кН. − v·c = 297,9 − 92,98· 0,99 = 205,9 кН.Проверяем условие Q = 205,9 кН < Qb + Qsw = 120,7 + 210,1 = 330,8 кН, то есть прочность по наклонным сечениям на действие поперечных сил у опоры А обеспечена. |
