1. составление разбивочной схемы сборного перекрытия
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
|
2.4.3. Расчет по прочности продольных ребер при действии поперечных сил Проверяем условие: Qmin > 0,5γb1·Rbt·b·h0, где Qmin – минимальное значение поперечной силы на опорах; 0,5γb1·Rbt·b·h0 соответствует образованию наклонной трещины. Минимальное значение поперечной силы на опорах Qmin = Q = 71,71 кН. 0,5γb1·Rbt·b·h0 = 0,5·0,9·1,05·103·0,185·0,355 = 31,03 кН, 71,71 кН > 31,03 кН, следовательно, поперечная арматура в продольных ребрах должна устанавливаться по расчету. Предварительно по конструктивным соображениям принимаем поперечную арматуру класса A240 с Rsw = 170 МПа. Согласно п. 10.3.13 диаметр поперечной арматуры в сварном каркасе подбирается из условия технологии сварки с наибольшим диаметром продольной арматуры. В двух плоских сварных каркасах при диаметре стержней продольной арматуры 22 мм поперечные стержни из условия технологии сварки принимаем диаметром 6 мм (dw ≥ 0,25d, по п. 5.8). В соответствии с п. 10.3.13 [3] шаг арматуры у опор должен быть не более: sw ≤ 0,5h0 = 0,5·355 = 177,5 мм; sw ≤ 300 мм. В соответствии с п. 3.2.22 шаг поперечной арматуры, учитываемой в расчете, должен быть не более: 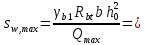 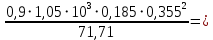 0,307 м, 0,307 м,где Qmax = Q = 71,71 кН. В расчет принимаем наименьшее значение шага поперечной арматуры с округлением в меньшую сторону кратно 50 мм. В первом приближении принимаем поперечную арматуру dw = 6 мм класса А240, с площадью поперечного сечения двух стержней Asw = 57 мм2 с шагом sw = 150 мм. Расчет продольных ребер по полосе между наклонными сечениями Расчет продольных ребер по бетонной полосе между наклонными сечениями производим из условия 3.59: Q < 0,3γb1·Rb·bр·h0, где Q – поперечная сила в нормальном сечении, принимаемом на расстоянии не менее h0 от опоры; ширина двух продольных ребер в среднем сечении b = 0,185 м. 0,3γb1·Rb·bр·h0 = 0,3·0,9·14,5·103·0,185·0,355 = 257,12 кН Q = Qоп − q·h0 = 71,71 − 36,0·0,355 = 58,93 кН 0,3γb1·Rb·bр·h0 = 257,12 кН > Q = 58,93 кН, т. е. прочность наклонной полосы на сжатие обеспечена. Расчет продольных ребер по наклонным сечениям на действие поперечных сил Расчет изгибаемых элементов по наклонному сечению производят из условия 3.44 [3]: Q ≤ Qb+ Qsw, где Q – поперечная сила в наклонном сечении с длиной проекции с на продольную ось элемента, определяемая от внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения; при вертикальной нагрузке приложенной к верхней грани элемента, значение Q принимается в нормальном сечении, проходящем на расстоянии c от опоры; при этом следует учитывать возможность отсутствия временной нагрузки на приопорном участке длиной c; Qb – поперечная сила, воспринимаемая бетоном в наклонном сечении; Qsw – поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении. Определяем усилие в поперечной арматуре на единицу длины элемента: 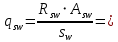 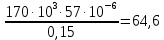 кН/м. кН/м.Поперечную арматуру учитывают в расчете, если соблюдается условие: 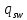 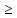 0,25γb1·Rbt·b, 0,25γb1·Rbt·b,0,25γb1·Rbt·b = 0,25·0,9·1,05·103·0,185 = 43,71 кН/м, 64,6 кН/м > 43,71 кН/м, условие выполняется, следовательно, поперечная арматура учитывается в расчете. Момент, воспринимаемый бетоном при действии поперечной силы: 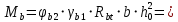 1,5·0,9·1,05·103· 0,185·0,3552 = 33,05 кН·м, 1,5·0,9·1,05·103· 0,185·0,3552 = 33,05 кН·м,где 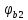 – коэффициент, принимаемый равным 1,5. – коэффициент, принимаемый равным 1,5.Определяем длину проекции невыгоднейшего наклонного сечения, согласно п. 3.2.19 [7]. При расчете элемента на действие равномерно распределенной нагрузки: qc принимают равным 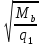 , а если при этом , а если при этом 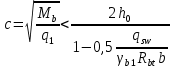 или или 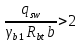 , следует принимать , следует принимать 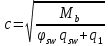 , где q1 = q при действии сплошной , где q1 = q при действии сплошнойравномерно распределенной нагрузки q; φsw – коэффициент, принимаемый равным 0,75. 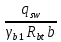 = = 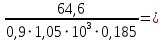 0,37 < 2, 0,37 < 2,с = 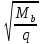 = = 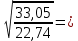 1,21 м > 1,21 м > 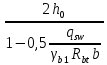 = = 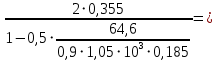 0,871 м; 0,871 м;тогда 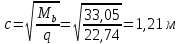 , что должно быть не менее h0 = 0,355 м и не более 3h0 = 3·0,355 = 1,065 м, , что должно быть не менее h0 = 0,355 м и не более 3h0 = 3·0,355 = 1,065 м,Длину проекции наклонной трещины с0 принимают равной с, но не менее h0 и не более 2h0. h0 = 0,355 м ≤ с0 ≤ 2h0 = 0,71 м. Принимаем с0 = с = 0,71 м. Определяем поперечную силу, воспринимаемую поперечной арматурой: Qsw = 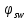 ·qsw·c0 = 0,75·64,6·0,71 = 34,4 кН. ·qsw·c0 = 0,75·64,6·0,71 = 34,4 кН.Находим поперечную силу, воспринимаемую бетоном: 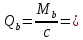 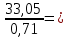 46,55 кН, 46,55 кН,но не более Qb,max = 2,5γb1·Rbt·b·h0 = 2,5·0,9·1,05·103·0,185·0,355 = 155,16 кН, и не менее Qb,min = 0, 5γb1·Rbt·b·h0 = 0,5·0,9·1,05·103·0,185·0,355 = 31,03 кН. Принимаем Qb = 46,55 кН. Определяем поперечную силу Q с учетом возможности отсутствия временной нагрузки на приопорном участке длиной с: Q = Qоп − 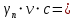 71,71 – 1,0·14,4·1,232·0,71 = 56,44 кН, 71,71 – 1,0·14,4·1,232·0,71 = 56,44 кН,где v – расчетная временная нагрузка в кН/м (v из табл. 2 (кН/м2), умноженная на bп (м)). Q = 56,44 кН < Qb + Qsw = 46,55 + 34,4 = 80,95 кН, то есть прочность по наклонным сечениям на действие поперечных сил у опор обеспечена. Принятая поперечная арматура с принятым шагом устанавливается на приопорных участках, равных четверти пролета, иначе – увеличиваем диаметр поперечной арматуры или уменьшаем шаг. Максимально допустимый шаг стержней поперечной арматуры в пролете балок высотой 150 мм и более в соответствии с п. 10.3.13 [3]: sw ≤ 0,75h0 = 0,75·355 = 266 мм; sw ≤ 500 мм. Принимаем наименьшее значение шага поперечной арматуры с округлением в меньшую сторону кратно 50 мм – sw = 250 мм. Окончательно устанавливаем в продольных ребрах плиты на приопорных участках длиной 0,25lпоперечную арматуру диаметром 6 мм класса А240 с шагом 150 мм, а на средних участках с шагом 250 мм. Поскольку продольная растянутая арматура ребер по концам приварена к закладным деталям, проверку наклонных сечений на действие момента не производим. 2.5. Расчет ребристой плиты по предельным состояниям второй группы Расчеты по предельным состояниям второй группы включают: − расчет по образованию трещин; − расчет по раскрытию трещин; − расчет по деформациям. 2.5.1. Определение геометрических характеристик приведенного сечения Приведенное сечение – сечение, имеющее два или более разнородных материалов, которые для удобства расчетов приводят к сечению с одним материалом, используя коэффициент приведения. Сжатую арматуру (A′s) в расчетах характеристик приведенного сечения условно не учитываем. Коэффициент приведения арматуры к бетону: 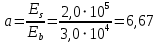 . .Площадь приведенного сечения: Ared= A1 + A2 + Asb = b · h + ( 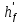 −b) · −b) · 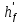 + α · As = + α · As == 185 ·400 + (1192 - 185) · 40 + 6,67 · 760 = 119349 мм2, где b = 185 мм – средняя толщина двух продольных ребер. Статический момент площади приведенного поперечного сечения элемента относительно наиболее растянутого волокна бетона (нижней грани сечения): 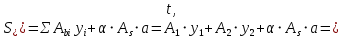 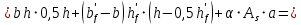 = 185 · 400 · 0,5 · 400 + (1192 - 185) · 40 · (400 – 0,5 · 40) + 6,67 · 760 · 45 = 30334514 мм3. Расстояние от наиболее растянутого волокна бетона до центра тяжести приведенного сечения: 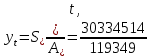 = 254,2 мм. = 254,2 мм.Момент инерции приведенного сечения относительно его центра тяжести: 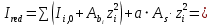 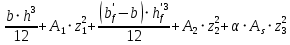 , ,где zi – расстояние от центра тяжести приведенного сечения до i-го прямоугольника; Ii,0 – собственный момент инерции каждого i-го элемента. 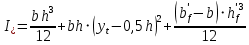 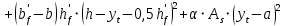 , ,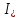 = = 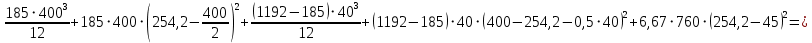 2068731186 мм4 = 2,06 · 109 мм4. 2068731186 мм4 = 2,06 · 109 мм4.Упругий момент сопротивления приведенного сечения: 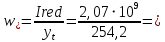 8,14 8,14  106 мм4. 106 мм4.2.5.2. Расчет по образованию трещин, нормальных к продольной оси Для железобетонных элементов, в которых допускается образование трещин, расчет по образованию трещин имеет вспомогательное значение и сводится к определению усилия, соответствующего образованию трещин [10], которое используется в дальнейших расчетах по раскрытию трещин и по деформациям. В этом случае коэффициент надежности по нагрузке γf принимается равным 1,0. Согласно п. 8.2.4 [3] расчет железобетонных элементов по образованию трещин производят из условия: Mn > Mcrc, где Mn – изгибающий момент от внешней нагрузки (γf = 1,0); Mcrc – изгибающий момент, воспринимаемый нормальным сечением элемента при образовании трещин. Если условие (1) выполняется, то в продольных ребрах ребристой плиты образуются трещины, необходимо выполнить расчеты по раскрытию трещин и по деформациям (прогибам); иначе – трещины не образуются, тогда необходимо выполнить расчет по деформациям (прогибам), а кривизна определяется на участках без трещин в растянутой зоне. Для тавровых сечений с полкой, расположенной в сжатой зоне, значение упругопластического момента сопротивления сечения для крайнего растянутого волокна при действии момента в плоскости оси симметрии допускается принять равным: Wpl = Wred·γ = 8,14·106·1,3 = 10,58·106 мм3, где γ – коэффициент, учитывающий неупругие деформации растянутого бетона, определяемый по табл. табл. 4.1, равный 1,3 для таврового сечения с полкой, расположенной в сжатой зоне. Момент образования трещин с учетом неупругих деформаций растянутого бетона определяется по формуле: Mcrc = Rbt,ser· Wpl = 1,55·10,58·106 = 16,4·106 Н·мм = 16,4 кН·м. Проверяем условие: Mn > Mcrc 95,12 кН·м > 16,4 кН·м, условие выполняется, следовательно, образуются трещины, необходимо проверить ширину их раскрытия. 2.5.3. Расчет по раскрытию трещин, нормальных к продольной оси Расчет железобетонных элементов производят по непродолжительному и продолжительному раскрытию трещин. Непродолжительное раскрытие определяют от совместного действия постоянных и временных (длительных и кратковременных) нагрузок, продолжительное – только от постоянных и временных длительных нагрузок. Согласно п. 8.2.6 расчет железобетонных элементов по раскрытию трещин производят из условия: acrc ≤ acrc,ult, где acrc – ширина раскрытия трещин от действия внешней нагрузки; acrc,ult – предельно допустимая ширина раскрытия трещин. Из условия обеспечения сохранности арматуры классов A240…A600, В500 acrc,ult принимается равным: 0,3 мм – при продолжительном раскрытии трещин; 0,4 мм – при непродолжительном раскрытии трещин. При отсутствии требований к конструкции по ограничению проницаемости и при выполнении условия (4.32) п. 4.14: 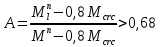 выполнить расчет можно только на продолжительность раскрытие трещин. выполнить расчет можно только на продолжительность раскрытие трещин.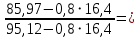 0,89 > 0,68 0,89 > 0,68Значит считаем только на продолжительность раскрытие трещин. Для тавровых сечений напряжение σs(напряжение в продольной растянутой арматуре в нормальном сечении с трещиной от соответствующей внешней нагрузки) допускается определять по формуле: 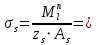 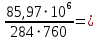 398,3 МПа, 398,3 МПа,где zs (плечо внутренней пары сил (расстояние от центра тяжести растянутой арматуры до точки приложения равнодействующей усилий в сжатой зоне сечения над трещиной)) = 0,8h0 = 0,8·355 = 284 мм. Находим высоту растянутой зоны бетона: 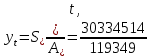 = 254,2 мм. = 254,2 мм.2a ≤ y = k·yt ≤ 0,5h, где k – поправочный коэффициент, учитывающий неупругие деформации растянутого бетона; для таврового сечения с полкой в сжатой зоне k = 0,9 2a = 2·45 = 90 мм < y = 0,9·254,2 = 228,8 мм > 0,5h = 200 мм, Принимаем y = 200 мм. Площадь сечения растянутого бетона: Abt = b·y = 185·200 = 37000 мм2. Базовое расстояние между трещинами: 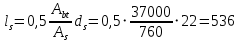 мм. мм.Полученное значение сравниваем с граничными значениями базового расстояния между трещинами: 10·ds = 10·22 = 220 мм ≤ ls ≤ 40·ds = 40·22 = 880 мм, 100 мм ≤ ls ≤ 400 мм. Принимаем ls = 400 мм. Коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами: 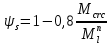 = = 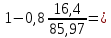 0,85, что больше чем 0,2. 0,85, что больше чем 0,2.Определяем ширину раскрытия трещин от продолжительного действия постоянных и временных длительных нагрузок: 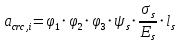 , ,где φ1 – коэффициент, учитывающий продолжительность действия нагрузки: 1,0 – при непродолжительном действии нагрузки; 1,4 – при продолжительном действии нагрузки; φ2 – коэффициент, учитывающий профиль продольной арматуры: 0,5 – для арматуры периодического профиля и канатной; 0,8 – для гладкой арматуры; φ3 – коэффициент, учитывающий характер нагружения элементов: 1,0 – для изгибаемых и внецентренно сжатых; 1,2 – для растянутых. 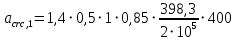 = 0,474 мм. = 0,474 мм.Определяем ширину продолжительного раскрытия трещин: acrc = acrc1 = 0,474 мм, что больше предельно допустимой ширины продолжительного раскрытия трещин acrc,ult = 0,3 мм, соответственно увеличиваем диаметр продольной рабочей арматуры в ребрах плиты до двух стрежней большего диаметра, но не более 28 мм, поскольку при диаметре 32 мм и более не обеспечиваются требования к минимальной толщине защитного слоя бетона по боковым граням ребер. устанавливаем в продольных ребрах по одному пучку из двух стержней (Ø20+ Ø18), всего 2Ø20+2Ø18 площадью 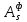 = 628 + 509 = 1137 мм2 > 759 мм2. = 628 + 509 = 1137 мм2 > 759 мм2.h0 = h − a = 400 − 50 = 350 мм, где a = 30 + 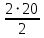 = 50 мм. = 50 мм.Расчет по прочности продольных ребер при действии поперечных сил Проверяем условие: Qmin > 0,5γb1·Rbt·b·h0, Qmin = 71,71 кН > 0,5·0,9·1,05·103·0,185·0,350 = 30,59 кН, 71,71 кН > 30,59 кН, следовательно, поперечная арматура в продольных ребрах должна устанавливаться по расчету. В двух плоских сварных каркасах при диаметре стержней продольной арматуры 22 мм поперечные стержни из условия технологии сварки принимаем диаметром 6 мм (dw ≥ 0,25·d, по п. 5.8). В соответствии с п. 10.3.13 [3] шаг арматуры у опор должен быть не более: sw ≤ 0,5h0 = 0,5·350 = 175 мм; sw ≤ 300 мм. В соответствии с п. 3.2.22 шаг поперечной арматуры, учитываемой в расчете, должен быть не более: 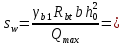 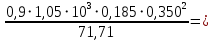 0,299 м = 299 мм, 0,299 м = 299 мм,где Qmax = Q = 71,71 кН. Во втором приближении принимаем поперечную арматуру dw = 6 мм класса А240, с площадью поперечного сечения двух стержней Asw = 57 мм2 с шагом sw = 150 мм. Расчет продольных ребер по полосе между наклонными сечениями Расчет продольных ребер по бетонной полосе между наклонными сечениями производим из условия 3.59: Q < 0,3γb1·Rb·bр·h0, где Q – поперечная сила в нормальном сечении, принимаемом на расстоянии не менее h0 от опоры; ширина двух продольных ребер в среднем сечении b = 0,185 м. 0,3γb1·Rb·bр·h0 = 0,3·0,9·14,5·103·0,185·0,350 = 253,5 кН Q = Qоп − q·h0 = 71,71 − 22,74·0,350 = 63,07кН 0,3γb1·Rb·bр·h0 = 253,5 кН > Q = 63,07 кН, т. е. прочность наклонной полосы на сжатие обеспечена. Расчет продольных ребер по наклонным сечениям на действие поперечных сил Расчет изгибаемых элементов по наклонному сечению производят из условия 3.44 [3]: Q ≤ Qb+ Qsw, Определяем усилие в поперечной арматуре на единицу длины элемента: 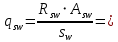 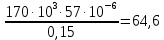 кН/м. кН/м.Поперечную арматуру учитывают в расчете, если соблюдается условие: 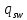 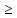 0,25γb1·Rbt·b, 0,25γb1·Rbt·b,0,25γb1·Rbt·b = 0,25·0,9·1,05·103·0,185 = 43,71 кН/м, 64,6 кН/м > 43,71 кН/м, условие выполняется, следовательно, поперечная арматура учитывается в расчете. Момент, воспринимаемый бетоном при действии поперечной силы: 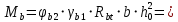 1,5·0,9·1,05·103· 0,185·0,3502 = 32,12 кН·м, 1,5·0,9·1,05·103· 0,185·0,3502 = 32,12 кН·м,Определяем длину проекции невыгоднейшего наклонного сечения, согласно п. 3.2.19 [7]. При расчете элемента на действие равномерно распределенной нагрузки: 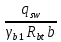 = = 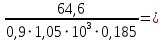 0,370 < 2, 0,370 < 2,с = 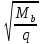 = = 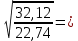 1,188 м > 1,188 м > 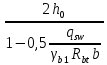 = = 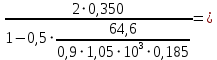 0,859 м; 0,859 м;тогда с = 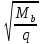 = = 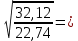 1,188 м , что должно быть не менее h0 = 0,350 м и не более 3h0 = 3·0,345 = 1,050 м, 1,188 м , что должно быть не менее h0 = 0,350 м и не более 3h0 = 3·0,345 = 1,050 м,Длину проекции наклонной трещины с0 принимают равной с, но не менее h0 и не более 2h0. h0 = 0,350 м ≤ с0 ≤ 2h0 = 0,7 м. Принимаем с0 = с = 0,7 м. Определяем поперечную силу, воспринимаемую поперечной арматурой: Qsw = 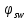 ·qsw·c0 = 0,75·64,6·0,7 = 33,92 кН. ·qsw·c0 = 0,75·64,6·0,7 = 33,92 кН.Находим поперечную силу, воспринимаемую бетоном: 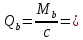 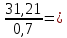 44,59 кН, 44,59 кН,но не более Qb,max = 2,5γb1·Rbt·b·h0 = 2,5·0,9·1,05·103·0,185·0,345 = 150,79 кН, и не менее Qb,min = 0, 5γb1·Rbt·b·h0 = 0,5·0,9·1,05·103·0,185·0,345 = 30,16 кН. Принимаем Qb = 44,59 кН. Определяем поперечную силу Q с учетом возможности отсутствия временной нагрузки на приопорном участке длиной с: Q = Qоп − 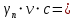 71,71 – 1,0·14,4·1,232·0,7 = 59,29 кН, 71,71 – 1,0·14,4·1,232·0,7 = 59,29 кН,Q = 59,29 кН < Qb + Qsw = 44,59 + 33,92 = 78,51 кН, то есть прочность по наклонным сечениям на действие поперечных сил у опор обеспечена. Максимально допустимый шаг стержней поперечной арматуры в пролете балок высотой 150 мм и более в соответствии с п. 10.3.13 [3]: sw ≤ 0,75h0 = 0,75·350 = 263 мм; sw ≤ 500 мм. Принимаем наименьшее значение шага поперечной арматуры с округлением в меньшую сторону кратно 50 мм – sw = 250 мм. Окончательно устанавливаем в продольных ребрах плиты на приопорных участках длиной 0,25lпоперечную арматуру диаметром 6 мм класса А240 с шагом 150 мм, а на средних участках с шагом 250 мм. Поскольку продольная растянутая арматура ребер по концам приварена к закладным деталям, проверку наклонных сечений на действие момента не производим. Определение геометрических характеристик приведенного сечения Приведенное сечение – сечение, имеющее два или более разнородных материалов, которые для удобства расчетов приводят к сечению с одним материалом, используя коэффициент приведения. Сжатую арматуру (A′s) в расчетах характеристик приведенного сечения условно не учитываем. Коэффициент приведения арматуры к бетону: 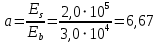 . .Площадь приведенного сечения: Ared= A1 + A2 + Asb = b · h + ( 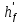 −b) · −b) · 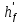 + α · As = + α · As == 185 ·400 + (1192 - 185) · 40 + 6,67 · 1137 = 121064 мм2, Статический момент площади приведенного поперечного сечения элемента относительно наиболее растянутого волокна бетона (нижней грани сечения): 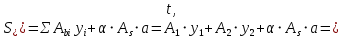 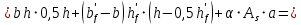 = 185 · 400 · 0,5 · 400 + (1192 - 185) · 40 · (400 – 0,5 · 40) + 6,67 · 1137 · 50 = 30485590 мм3. Расстояние от наиболее растянутого волокна бетона до центра тяжести приведенного сечения: 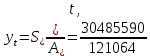 = 251,8 мм. = 251,8 мм.Момент инерции приведенного сечения относительно его центра тяжести: 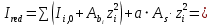 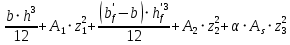 , ,где zi – расстояние от центра тяжести приведенного сечения до i-го прямоугольника; Ii,0 – собственный момент инерции каждого i-го элемента. 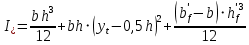 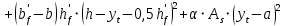 , ,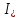 = = 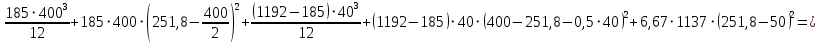 2161445061 мм4 = 2,16 · 109 мм4. 2161445061 мм4 = 2,16 · 109 мм4.Упругий момент сопротивления приведенного сечения: 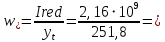 8,58 8,58  106 мм4. 106 мм4.Расчет по образованию трещин, нормальных к продольной оси Упругопластический момент сопротивления сечения для крайнего растянутого волокна при действии момента в плоскости оси симметрии допускается принять равным: Wpl = Wred·γ = 8,58·106·1,3 = 11,15·106 мм3, Момент образования трещин с учетом неупругих деформаций растянутого бетона: Mcrc = Rbt,ser· Wpl = 1,55·11,15·106 = 17,3·106 Н·мм = 17,3 кН·м. Проверяем условие: Mn > Mcrc 95,12 кН·м > 17,3 кН·м, условие выполняется, следовательно, образуются трещины, необходимо проверить ширину их раскрытия. Расчет по раскрытию трещин, нормальных к продольной оси Расчет железобетонных элементов производят по непродолжительному и продолжительному раскрытию трещин. Непродолжительное раскрытие определяют от совместного действия постоянных и временных (длительных и кратковременных) нагрузок, продолжительное – только от постоянных и временных длительных нагрузок. Согласно п. 8.2.6 расчет железобетонных элементов по раскрытию трещин производят из условия: Проверяем условие: 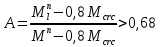 выполнить расчет можно только на продолжительность раскрытие трещин. выполнить расчет можно только на продолжительность раскрытие трещин.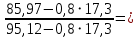 0,89 > 0,68 0,89 > 0,68Значит считаем только на продолжительность раскрытие трещин. Для тавровых сечений напряжение 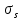 допускается определять по формуле: допускается определять по формуле: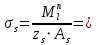 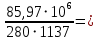 270 МПа, 270 МПа,где 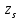 = 0,8h0 = 0,8·350 = 280 мм. = 0,8h0 = 0,8·350 = 280 мм.Находим высоту растянутой зоны бетона: 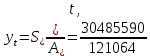 = 251,8 мм. = 251,8 мм.2a ≤ y = k·yt ≤ 0,5h, где k – поправочный коэффициент, учитывающий неупругие деформации растянутого бетона; для таврового сечения с полкой в сжатой зоне k = 0,9 2a = 2·50 = 100 мм < y = 0,9·251,8 = 226,6 мм > 0,5h = 200 мм, Принимаем y = 200 мм. Площадь сечения растянутого бетона: Abt = b·y = 185·200 = 37000 мм2. При различных диаметрах стержней растянутой арматуры значения ds определяется согласно п. 4.12: 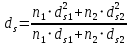 = = 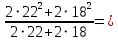 21 мм, 21 мм,где d1, d2 – диаметры стержней растянутой арматуры, равные 20 и 18 мм соответственно; n1, n2 – число стержней диаметрами соответственно d1 и d2. Базовое расстояние между трещинами: 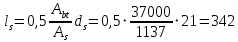 мм. мм.Полученное значение сравниваем с граничными значениями базового расстояния между трещинами: 10·ds = 10·21 = 210 мм ≤ ls ≤ 40·ds = 40·21 = 840 мм, 100 мм ≤ ls ≤ 400 мм. Принимаем ls = 342 мм. Коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами: 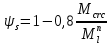 = = 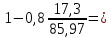 0,84, что больше чем 0,2. 0,84, что больше чем 0,2.Определяем ширину раскрытия трещин от продолжительного действия постоянных и временных длительных нагрузок: 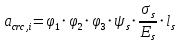 , ,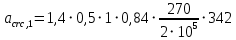 = 0,272 мм. = 0,272 мм.Определяем ширину продолжительного раскрытия трещин: acrc = acrc1 = 0, 272 мм, что меньше предельно допустимой ширины продолжительного раскрытия трещин acrc,ult= 0,3 мм, условие выполняется. |
