1. составление разбивочной схемы сборного перекрытия
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
|
2.3.2. Расчет рабочей продольной арматуры поперечного ребра При расчете поперечного ребра за расчетное принимаем тавровое сечение с полкой в сжатой зоне. При отношении толщины плиты к высоте ребра 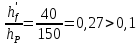 согласно п. 8.1.11 [3] ширина полки принимается не более: согласно п. 8.1.11 [3] ширина полки принимается не более: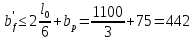 мм, мм,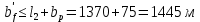 м, м,где bр – средняя толщина поперечного ребра. Применяем наименьшее значение. 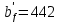 мм. мм.С пунктом 10.3.2 также необходимо учесть, что поперечное ребро армируется сварным каркасом, тогда минимальное расстояние до поверхности рабочей арматуры с учетом возможности приварки поперечных стержней каркаса к продольной арматуре составит 25 мм. Из всех условий принимаем максимальное значение толщины защитного слоя бетона – 25 мм. Рабочая высота сечения: h0 = hр − a = 150 − 30 = 120 мм, где a = 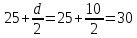 мм. мм.Определяем, где пройдет граница сжатой зоны в тавровом сечении: 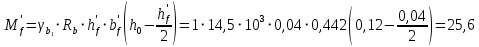 кНм кНмM = 1,91 кНм < M′f = 25,6 кНм. Условие выполняется, следовательно, граница сжатой зоны бетона пройдет в полке таврового сечения, в этом случае сечение рассчитывается как прямоугольное шириной 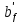 . .Находим относительную несущую способность сечения и проверяем условие αm ≤ αR: 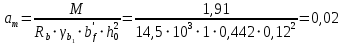 Определяем граничную относительную высоту сжатой зоны бетона и граничную относительную несущую способность для арматуры класса А500С: 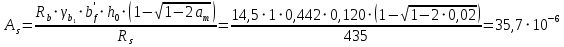 м2 = 35,7 мм2. м2 = 35,7 мм2.Принимаем в поперечных ребрах плоские сварные каркасы с продольной арматурой из стержней класса А500 с диаметром 8 мм с 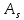 = 50,3 мм2. = 50,3 мм2.2.3.3. Расчет по прочности поперечного ребра при действии поперечных сил Проверяем условие: Qmin > 0,5γb1·Rbt·bр·h0 где Qmin – минимальное значение поперечной силы на опорах; 0,5γb1·Rbt·bр·h0 соответ- ствует образованию наклонной трещины. Если условие выполняется, то поперечную арматуру устанавливаем по расчету, иначе осуществляется конструктивное армиро- вание; bр – средняя толщина поперечного ребра. Минимальное значение поперечной силы на опорах Qmin = Q = 6,95 кН. 0,5γb1·Rbt·bр·h0 = 0,5·1·1,05·103·0,075·0,12 = 4,73 кН, 6,95 кН > 4,73 кН, При высоте ребра 150 мм и продольной арматуре диаметром 8 мм принимаем поперечные стержни в каркасах из арматуры класса А240 диаметром 6 мм с Аsw = 28,3 мм2. В соответствии с п. 10.3.13 [3] шаг арматуры должен быть не более: sw ≤ 0,5h0 = 0,5·120 = 60 мм; sw ≤ 300 мм. Принимаем шаг поперечных стержней в каркасах sw = 60 мм. Расчет поперечного ребра по полосе между наклонными сечениями Проверим прочность наклонной полосы между наклонными сечениями в соответствии с п. 8.1.32 [3] Q = 6,95 кН < 0,3γb1·Rb·bр·h0 = 0,3·1·14,5·103·0,075·0,120 = 39,15 кН. Прочность полосы на сжатие обеспечена. Расчет поперечного ребра по наклонным сечениям на действие поперечных сил Прочность наклонных сечений поперечных ребер по поперечной силе проверим согласно п. 8.1.33 [3]. Поскольку 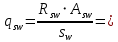 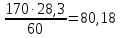 Н/мм > Н/мм > 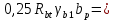 0,25 · 1,05 · 1 ·75 = 19,69 Н/мм, 0,25 · 1,05 · 1 ·75 = 19,69 Н/мм,хомуты учитываем в расчете полностью. Не соблюдение условия свидетельствует о том, что наклонная трещина образуется между поперечной арматурой, то есть в расчетное сечение не попадает ни один стержень поперечной арматуры. В этом случае поперечная сила должна восприниматься только бетоном, а разрушение будет носить хрупкий крайне нежелательный характер. Для предотвращения внезапного хрупкого разрушения по наклонному сечению на действие поперечной силы необходимо увеличить интенсивность поперечного армирования, то есть параметр qsw (увеличить диаметр поперечной арматуры или уменьшить ее шаг). Значение Мb определяется по формуле: Mb =1,5Rbt ⋅ γb1 ⋅bр ⋅ 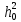 = 1,5⋅1,05⋅1⋅75⋅1202 =1,7⋅106 Н⋅мм. = 1,5⋅1,05⋅1⋅75⋅1202 =1,7⋅106 Н⋅мм.Определяем длину проекции невыгоднейшего наклонного сечения, согласно п. 3.2.19 [7]. При расчете элемента на действие равномерно распределенной нагрузки q значение c принимают равным 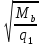 , а если при этом , а если при этом 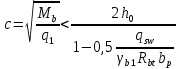 или или 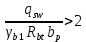 , следует принимать , следует принимать 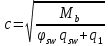 , где q1 = q − 0,5qν в случае если нагрузка включает в себя временную, приведенную к эквивалентной равномерно распределенной; φsw – коэффициент, принимаемый равным 0,75. , где q1 = q − 0,5qν в случае если нагрузка включает в себя временную, приведенную к эквивалентной равномерно распределенной; φsw – коэффициент, принимаемый равным 0,75.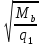 = = 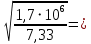 482 мм < 482 мм < 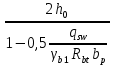 = = 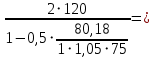 489 мм; 489 мм;тогда 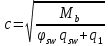 = = 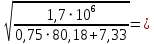 159 мм, что не менее h0 = 120 мм и не более 3h0 = 3·120 = 360 мм, 159 мм, что не менее h0 = 120 мм и не более 3h0 = 3·120 = 360 мм,где q1 = q − 0,5qν = 12,63 − 0,5·10,6 = 7,33 кН/м. Длину проекции наклонной трещины с0 принимают равной с, но не менее h0 и не более 2h0. h0 = 120 мм ≤ с0 ≤ 2h0 = 240 мм. Принимаем с0 = с = 159 мм. Находим поперечные силы, воспринимаемые бетоном и арматурой: Qsw = 0,75qsw·c0 = 0,75·80,18·159·10-3 = 9,6 кН, 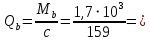 10,69 кН, 10,69 кН,но не более Qb,max = 2,5γb1·Rbt·bр·h0 = 2,5·1·1,05·103·0,075·0,120 = 23,63 кН, и не менее Qb,min = 0, 5γb1·Rbt·bр·h0 = 0,5·1·1,05·103·0,075·0,120 = 4,73 кН. Принимаем Qb = 10,69 кН. Qb + Qsw = 10,69 + 9,6 = 20,29 кН, Q = Qmax − q1c = 6,95 − 7,33·0,159 = 5,78 кН. Qb + Qsw = 20,39 кН > Q = 5,78 кН, следовательно, прочность наклонных сечений на действие поперечных сил обеспечена. В соответствии с п. 3.2.22 [7] шаг поперечной арматуры, учитываемой в расчете, должен быть не более: 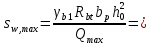 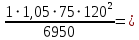 163,2 мм. 163,2 мм.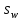 = 60 мм < = 60 мм < 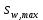 = 163,2 мм, следовательно, требование выполнено. = 163,2 мм, следовательно, требование выполнено.2.4. Расчет продольного ребра Высоту плит (продольных ребер) ориентировочно определяем из соотношения: 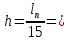 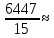 429 мм. 429 мм.Полученное значение высоты округляем в большую сторону с кратностью 50 мм, но ограничиваем h≤ 400 мм. Окончательно принимаем h = 400 мм. В соответствии с п. 7.5.6 [1] ребристые плиты рекомендуется применять высотой 300 или 400 мм. В качестве опорных конструкций для панелей принимаем ригели прямоугольного сечения с шириной ребра bриг = 300 мм. 2.4.1. Сбор нагрузок. Статический расчет продольного ребра
Сбор нагрузок на 1 м2 двух продольных ребер плиты перекрытия (*) 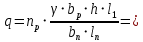 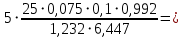 0,12 кН/м2, 0,12 кН/м2,(**) 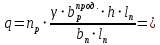 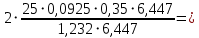 1,31 кН/м2, 1,31 кН/м2,где 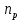 – количество поперечных или продольных ребер, шт. – количество поперечных или продольных ребер, шт.Погонная нагрузка на два продольных ребра: • полная расчетная нагрузка: q = γn ·18,46·bп = 1,0·18,46·1,232 = 22,74 кН/м, • постоянная и временная длительная расчетная нагрузка: ql = γn ·16,66·bп = 1,0·16,66·1,232 = 20,53 кН/м, • полная нормативная нагрузка: qn = γn ·15,53·bп = 1,0·15,53·1,232 = 19,13 кН/м, • постоянная и временная длительная нормативная: 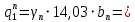 1,0·14,03·1,232 = 17,29 кН/м. 1,0·14,03·1,232 = 17,29 кН/м.За расчетную схему для продольных ребер принимаем однопролетную балку со свободным опиранием концов на ригели (рис. 7), расчетный пролет определяется как расстояние между серединами площадок опирания ребер плиты на ригели: l0 = l − 0,5·bриг = 6,457 − 0,5·0,3 = 6,307 м. Усилия в двух продольных ребрах: от полной расчетной нагрузки: 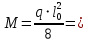 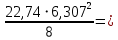 113,07 кН·м; 113,07 кН·м;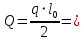 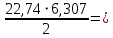 71,71 кН; 71,71 кН;от постоянной и временной длительной расчетной: 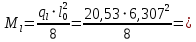 102,08 кН·м; 102,08 кН·м;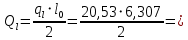 64,74 кН; 64,74 кН;от полной нормативной нагрузки: 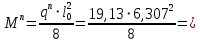 95,12 кН·м; 95,12 кН·м;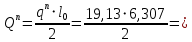 60,33 кН; 60,33 кН;от постоянной и временной длительной нормативной: 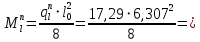 85,97 кН·м; 85,97 кН·м;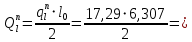 54,52 кН; 54,52 кН;в том числе, от кратковременной: 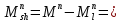 95,12 – 85,97 = 9,15 кН·м; 95,12 – 85,97 = 9,15 кН·м;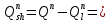 60,33 – 54,52 = 5,81 кН. 60,33 – 54,52 = 5,81 кН. 2.4.2. Расчет продольной рабочей арматуры продольных ребер Расчетное сечение двух продольных ребер – тавровое с полкой в сжатой зоне . При ширине продольных ребер по верху 100 мм и по низу 85 мм суммарная толщина двух ребер без учета швов замоноличивания будет равна: b = 2 · 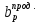 = 185 мм, = 185 мм,где 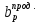 = 0,5 · (100 + 85) = 92,5 мм – средняя толщина продольного ребра. = 0,5 · (100 + 85) = 92,5 мм – средняя толщина продольного ребра.Ширина полки, вводимая в расчет, в соответствии с п. 8.1.11 [3] при наличии поперечных ребер: 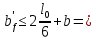 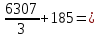 2287 мм; 2287 мм; bп = 1232 мм. bп = 1232 мм.Принимаем минимальное из двух значений  = 1232 мм. = 1232 мм.Работу бетона в швах замоноличивания в запас прочности условно не учитываем, предполагая, что при неблагоприятных условиях надежная совместная работа бетона замоноличивания с продольными ребрами за счет их сцепления может быть не обеспечена. Тогда расчетная ширина полки:  = bп − 2·20 = 1232 − 40 = 1192 мм. = bп − 2·20 = 1232 − 40 = 1192 мм.В соответствии с п. 10.3.2 [3] минимальное значение толщины защитного слоя бетона следует принимать: – не менее 15 мм, для сборных железобетонных конструкций, эксплуатируемых в закрытых помещениях при нормальной и пониженной влажности, поскольку для сборных элементов значение из табл. 10.1 [3] (20 мм) уменьшают на 5 мм; – не менее диаметра стержня (предполагаем, что максимальный диаметр рабочей арматуры 28 мм); – не менее 10 мм. Также учитываем, что продольная рабочая арматура на опоре приваривается к закладной детали, от размеров которой, будет зависеть величина защитного слоя бетона, равная в данном случае 30 мм. Принимаем толщину защитного слоя бетона 30 мм. Рабочая высота сечения: h0 = h − a = 400 − 45 = 355 мм, где a = 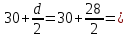 44 мм 44 мм  45 мм. 45 мм.С ≤ ≤ огласно п. 6.1.12 [3] определяем коэффициент условий работы бетона  , который зависит от соотношения усилий (изгибающего момента) от постоянных и длительных нагрузок к усилию от полных нагрузок: , который зависит от соотношения усилий (изгибающего момента) от постоянных и длительных нагрузок к усилию от полных нагрузок:Ml > 0,9 → γb1 = 0,9; M ≤ 0,9 → γb1 = 1. 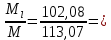 0,903 > 0,9, следовательно, коэффициент условий работы 0,903 > 0,9, следовательно, коэффициент условий работы 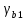 = 0,9. = 0,9.Расчет производим в предположении, что сжатая арматура по расчету не требуется A′s = 0. Определим, где проходит граница сжатой зоны бетона. 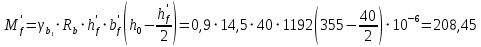 кНм кНмт.к. 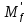 = 208,45 кН·м > M = 113,07 кН·м, следовательно, нейтральная ось проходит в = 208,45 кН·м > M = 113,07 кН·м, следовательно, нейтральная ось проходит впределах полки (x < 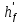 ) и элемент рассчитывается как прямоугольный с шириной ) и элемент рассчитывается как прямоугольный с шириной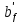 = 1192 мм. = 1192 мм.Находим относительную несущую способность сечения: 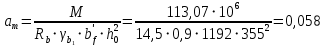 . .Проверяем условие αm ≤ αR, если условие не выполняется, то требуется увеличить сечение, повысить класс бетона или установить сжатую арматуру. Определяем граничную относительную высоту сжатой зоны бетона и граничную относительную несущую способность для арматуры класса А500С: 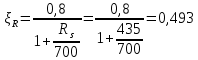 ; ;αR =  (1 - 0,5 · (1 - 0,5 ·  ) = 0,493(1 - 0,5·0,493) = 0,371, ) = 0,493(1 - 0,5·0,493) = 0,371,т.к. αm = 0,058 < αR = 0,371, то сжатая арматура по расчету не требуется. Определяем требуемое количество продольной арматуры класса А500С: 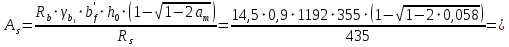 759 мм2. 759 мм2.В качестве продольной рабочей арматуры принимаем стержни 2Ø22 класса А500С площадью больше требуемой Asф = 760 мм2 > 759 мм2. Монтажную арматуру в каркасах продольных ребер принимаем 2Ø10 класса А240 площадью 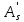 = 157 мм2. = 157 мм2. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

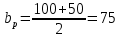 мм,
мм,