1. составление разбивочной схемы сборного перекрытия
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
|
Расчет ригеля по наклонным сечениям на действие моментов Расчет на действие момента производят для наклонных сечений, расположенных в местах обрыва продольной арматуры, а также у грани крайней свободной опоры балок и у свободного конца консолей при отсутствии у продольной арматуры специальных анкеров. Расчет железобетонных элементов по наклонным сечениям на действие моментов производят из условия: M ≤ Ms + Msw, где M – момент в наклонном сечении с длинной проекции c на продольную ось элемента, определяемый от внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения, относительно конца наклонного сечения, противоположного концу, у которого располагается проверяемая продольная арматура, испытывающая растяжение от момента в наклонном сечении; Ms – момент, воспринимаемый продольной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения; Msw – момент, воспринимаемый поперечной арматурой, пересекающей наклонное сечение, относительно противоположного наклонного сечения. В первом приближении выполняем расчет ригеля по наклонному сечению на действие момента из условия, что у грани крайней свободной опоры ригеля (опоры А) верхний ряд нижней арматуры (3Ø18 мм) не доводим до опоры, а у оставшегося нижнего ряда арматуры (3Ø25 мм) отсутствуют специальные анкера. Определяем расстояние от конца продольной арматуры до точки пересечения с ней наклонного сечения: ls = lsup − 30 = 380 − 30 = 350 мм, где 30 мм – защитный слой в торце продольного стержня на опоре. Определяем расчетное сопротивление сцепления арматуры с бетоном: Rbond = η1·η2·Rbt· 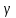 b1 = 2,5·1,0·1,05·0,9 = 2,36 МПа, b1 = 2,5·1,0·1,05·0,9 = 2,36 МПа,где η1 – коэффициент, учитывающий влияние вида поверхности арматуры, принимаемый равным 2,5 для горячекатаной арматуры периодического профиля (класса А500С); η2 – коэффициент, учитывающий влияние размера диаметра арматуры, принимаемый равным 1,0 при диаметре продольной арматуры ds ≤ 32 мм (диаметр продольной арматуры 25 мм). Базовую (основную) длину анкеровки, необходимую для передачи усилия в арматуре с полным расчетным значением сопротивления Rs на бетон, определяем по формуле: 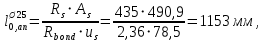 где As и us – соответственно площадь поперечного сечения одного анкеруемого стержня и периметр его сечения, определяемые по номинальному диаметру стержня. Анкеруемый арматурный стержень в крайнем пролете диаметром 25 мм, площадью поперечного сечения As = 490,9 мм2, периметром us = π·d = π·25 = 78,5 мм. Устанавливаем значение коэффициента α, учитывающего влияние на длину анкеровки напряженного состояния бетона и арматуры, и конструктивного решения элемента в зоне анкеровки. Для ненапрягаемой арматуры при анкеровке стрежней периодического профиля с прямыми концами без дополнительных анкерующих устройств для растянутых стрежней принимают α = 1,0. Определяем длину анкеровки по формуле: 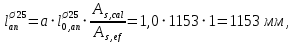 где 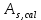 и и 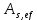 – площади поперечного сечения арматуры, требуемая по расчету и фактически установленная соответственно, для данного расчета принимается – площади поперечного сечения арматуры, требуемая по расчету и фактически установленная соответственно, для данного расчета принимается 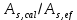 = 1. = 1.В любом случае фактическая длина анкеровки принимается: lan ≥ 15ds = 15·25 = 375 мм; lan ≥ 200 мм; lan ≥ 0,3 l0,an = 0,3·1153 = 345,9 мм. Принимаем 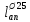 = 1153 мм. = 1153 мм.При пересечении наклонного сечения продольной растянутой арматурой, не имеющей анкеров в пределах зоны анкеровки, усилие Ns определяется по формуле: 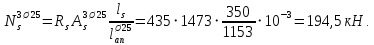 В случае приваривания к продольным растянутым стержням поперечной арматуры Ns увеличивается на величину усилия Nw, связанного с сопротивлением бетона раскалыванию от действия поперечных сил анкерующих стержней 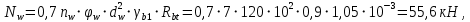 где 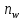 – количество приваренных стержней по длине ls; dw – диаметр привариваемых стержней (поперечной арматуры); φw – коэффициент, принимаемый по табл. 3.4 [7] в зависимости от dw. Принимаем dw = 10 мм, nw = 2·3+1=7, φw = 120. – количество приваренных стержней по длине ls; dw – диаметр привариваемых стержней (поперечной арматуры); φw – коэффициент, принимаемый по табл. 3.4 [7] в зависимости от dw. Принимаем dw = 10 мм, nw = 2·3+1=7, φw = 120.Но не более усилия, связанного с прочностью самих поперечных анкерующих стержней 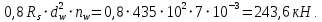 Принимаем 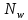 = 55,6 кН. = 55,6 кН.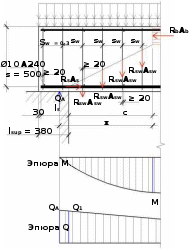 Тогда усилие в продольной растянутой арматуре Ns будет равно 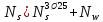 = 194,5 + 55, 6 = 250,1 кН. = 194,5 + 55, 6 = 250,1 кН.При этом значение Ns принимается не более максимального значения Ns,max, вычисленного по тем же формулам при α = 0,7. 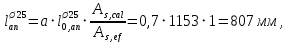 В любом случае фактическая длина анкеровки принимается: lan ≥ 15ds = 15·25 = 375 мм; lan ≥ 200 мм; lan ≥ 0,3 l0,an = 0,3·807 = 242 мм. Принимаем 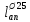 = 807 мм. = 807 мм.Находим максимальное значение усилия в продольной растянутой арматуре: 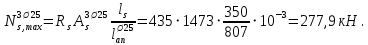 Принимаем Ns = 250,1 кН. Определим плечо внутренней пары сил: 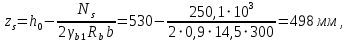 при наличии сжатой арматуры zs ≥ h0 − a′ = 530 – 42 = 488 мм. Принимаем 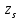 = 498 кН. = 498 кН.Момент, воспринимаемый продольной арматурой, определяем по формуле: Ms = Ns·zs = 250,1·498·10-3 = 124,6 кН·м. Усилие в поперечной арматуре на единицу длины элемента: 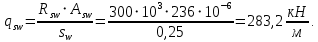 Поперечная сила в начале наклонного сечения 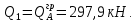 Определим длину проекции невыгоднейшего наклонного сечения при действии равномерно распределенной нагрузки по формуле: 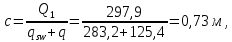 кроме того, с принимают в пределах h0 = 0,53 м ≤ с ≤ 2h0 = 2·0,53 = 1,06 м. Принимаем с = 0,73 м. Момент, воспринимаемый поперечной арматурой, определяем по формуле: Msw = 0,5qswc2 = 0,5·283,2·0,732 = 75,5 кН·м. Момент в наклонном сечении определяем как момент в нормальном сечении, расположенном в конце наклонного сечения, то есть на расстоянии от точки приложения опорной реакции, равной: 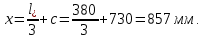 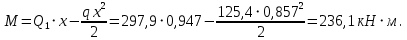 Проверяем условие: M = 236,1 кН·м > Ms + Msw = 124,6 + 75,5 = 200,1 кН·м, условие не выполняется, т.е. если верхний ряд нижней арматуры (3Ø25 мм) не доводим до опоры, а у оставшегося нижнего ряда арматуры (3Ø18 мм) отсутствуют специальные анкера, то прочность по наклонным сечениям на действие моментов у опоры А не обеспечена. Во втором приближении выполняем расчет из условия, что все 6 стрежней продольной рабочей арматуры (3Ø25 мм и 3Ø18 мм) доведены до свободной опоры ригеля А. Определяем базовую (основную) длину анкеровки, необходимую для передачи усилия в арматуре диаметром 25 мм с полным расчетным значением сопротивления Rs на бетон: 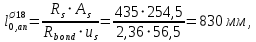 где As и us – соответственно площадь поперечного сечения одного анкеруемого стержня и периметр его сечения, определяемые по номинальному диаметру стержня. Анкеруемый арматурный стержень в крайнем пролете диаметром 18 мм, площадью поперечного сечения As = 254,5 мм2, периметром us = π·d = π·18 = 56,5 мм. Принимаем коэффициент α = 1,0 и определяем длину анкеровки: 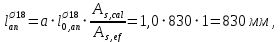 В любом случае фактическая длина анкеровки принимается: lan ≥ 15ds = 15·18 = 270 мм; lan ≥ 200 мм; lan ≥ 0,3 l0,an = 0,3·830 = 249 мм. Принимаем 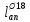 = 830 мм. = 830 мм.Определяем усилие в продольной растянутой арматуре: 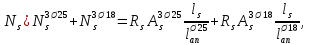 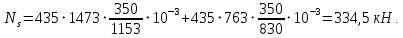 С учетом поперечной арматуры: 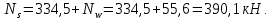 Определяем максимально допустимое значение усилия Ns,max, вычисленного по тем же формулам при α = 0,7. 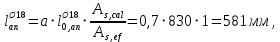 В любом случае фактическая длина анкеровки принимается: lan ≥ 15ds = 15·18 = 270 мм; lan ≥ 200 мм; lan ≥ 0,3 l0,an = 0,3·581 = 174 мм. Принимаем 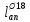 = 581 мм. = 581 мм.Находим максимальное значение усилия в продольной растянутой арматуре: 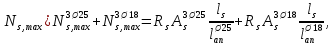 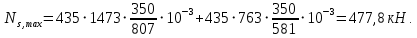 Принимаем 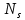 = 390,1 кН. = 390,1 кН.Определим плечо внутренней пары сил: 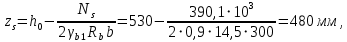 при наличии сжатой арматуры zs ≥ h0 − a′ = 530 – 42 = 488 мм. Принимаем 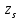 = 488 кН. = 488 кН.Момент, воспринимаемый продольной арматурой, определяем по формуле: Ms = Ns·zs = 390,1·488·10-3 = 190,4 кН·м. Проверяем условие M = 236,1 кН·м < Ms + Msw = 190,4 + 75,5 = 265,9 кН·м, условие выполняется, т. е. если все 6 стрежней продольной рабочей арматуры (3Ø25 мм и 3Ø18 мм) доведены до свободной опоры ригеля А, прочность по наклонным сечениям на действие моментов у опоры А обеспечена. В третьем приближении выполняем расчет из условия, что у грани крайней опоры ригеля у нижнего ряда арматуры (3Ø25 мм) на концах стержней устраиваются специальные анкера в виде пластин, шайб, гаек, уголков, высаженных головок и т. п., удовлетворяющих требованиям п. 5.36 [7] или концы стержней привариваются к надежно заанкеренным закладным деталям, а верхний ряд нижней арматуры (3Ø18 мм) не доводится до опоры. Пересчитываем значение усилия Ns: 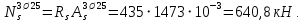 Определим плечо внутренней пары сил: 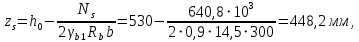 при наличии сжатой арматуры zs ≥ h0 − a′ = 530 – 42 = 488 мм. Принимаем 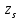 = 488 кН. = 488 кН.Момент, воспринимаемый продольной арматурой, определяем по формуле: Ms = Ns·zs = 640,8·488·10-3 = 312,7 кН·м. Проверяем условие M = 236,1 кН·м < Ms + Msw = 312,7 + 75,5 = 388,2 кН·м, условие выполняется, то есть прочность по наклонным сечениям на действие моментов у опоры А при установке на концах стержней нижнего ряда специальных анкеров обеспечена. Таким образом, для обеспечения прочности наклонных сечений на действие изгибающего момента необходимо всю продольную арматуру нижней зоны в крайнем пролете со стороны опоры А довести до конца ригеля или у нижнего ряда арматуры (3Ø25 мм) со стороны опоры А предусматреть устройство на концах стержней специальных анкеров в виде пластин, шайб, гаек, уголков, высаженных головок и т. п. 3.4.3. Определение шага поперечной арматуры в средней части крайнего и среднего пролетов Шаг поперечной арматуры в средней части крайнего и среднего пролетов ригеля определяем по наибольшему значению поперечной силы Q1 на расстоянии ¼ пролета от оси опоры. • Величина Q1 для крайнего пролета: 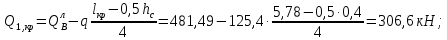 • Величина Q1 для среднего пролета: 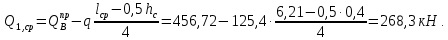 Принимаем Q1 = 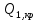 = = 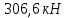 . .Момент, воспринимаемый бетоном при действии поперечной силы: 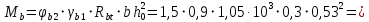 119,5 кН 119,5 кН  м. м.Определяем длину проекции невыгоднейшего наклонного сечения: 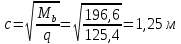 , но не менее h0 и не более 3h0. , но не менее h0 и не более 3h0.h0 = 0,53 м ≤ с ≤ 3h0 = 3·0,53 = 1,59 м. Принимаем c = 1,25 м. Поперечная сила, воспринимаемая бетоном: 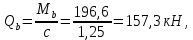 но не более Qb,max = 2,5γb1·Rbt·b·h0 = 2,5·0,9·1,05·103·0,3·0,53 = 375,6 кН, и не менее Qb,min = 0,5γb1·Rbt·b·h0 = 0,5·0,9·1,05·103·0,3·0,53 = 75,1 кН. Принимаем Qb = 157,3 кН. Проверяем условие Q1 = 306,6 кН > Qb = 157,3 кН, т. е. поперечная сила не может быть воспринята только бетоном. Максимально допустимый шаг стержней поперечной арматуры в элементах, в которых поперечная сила не может быть воспринята только бетоном: sw ≤ 0,5h0 = 0,5·530 = 265 мм; sw ≤ 300 мм. В соответствии с п. 3.2.22 шаг поперечной арматуры, учитываемой в расчете, должен быть не более: 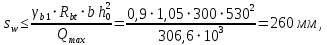 где Qmax = 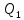 = 306,6 кН. = 306,6 кН.В расчет принимаем наименьшее значение шага поперечной арматуры с округлением в меньшую сторону кратно 50 мм. Принимаем поперечную арматуру dw = 10 мм класса А500C, с площадью поперечного сечения трех стержней Asw = 236 мм2 с шагом sw = 250 мм. Определяем усилие в поперечной арматуре на единицу длины элемента:: 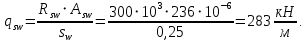 Поперечную арматуру учитывают в расчете, если соблюдается условие: qsw ≥ 0,25·γb1·Rbt·b, 0,25γb1·Rbt·b = 0,25·0,9·1,05·103·0,3 = 70,9 кН/м, 283 кН/м > 70,9 кН/м, условие выполняется, следовательно, поперечная арматура учитывается в расчете. Определяем длину проекции невыгоднейшего наклонного сечения: 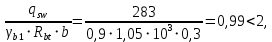 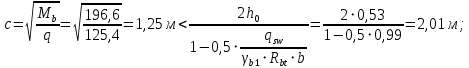 тогда 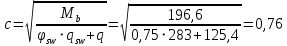 м, но не менее h0 и не более 3h0. м, но не менее h0 и не более 3h0.h0 = 0,53 м ≤ с ≤ 3h0 = 3·0,53 = 1,59 м. Принимаем c = 0,76 м. Длину проекции наклонной трещины c0 принимают равным c, но не менее h0 и не более 2h0. h0 = 0,53 м ≤ с ≤ 2h0 = 2·0,53 = 1,06 м. Принимаем c = c0 = 0,76 м. Поперечная сила, воспринимаемая поперечной арматурой: Qsw = φsw·qsw·c0 = 0,75·236·0,76 = 134,5 кН. Поперечная сила, воспринимаемая бетоном: 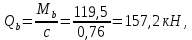 но не более Qb,max = 2,5γb1·Rbt·b·h0 = 2,5·0,9·1,05·103·0,3·0,53 = 375,4 кН, и не менее Qb,min = 0,5γb1·Rbt·b·h0 = 0,5·0,9·1,05·103·0,3·0,53 = 75,1 кН. Принимаем Qb = 157,2 кН. Проверяем условие Q1 = 306,6 кН > Qb + Qsw = 157,2 + 134,5 = 291,7 кН, то есть прочность по наклонным сечениям на действие поперечных сил в средней части крайнего пролета ригеля не обеспечена. Уменьшаем шаг поперечной арматуры до sw = 200 мм и выполняем перерасчет. Определяем усилие в поперечной арматуре на единицу длины элемента: 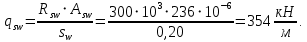 Поперечную арматуру учитывают в расчете, если соблюдается условие: qsw ≥ 0,25·γb1·Rbt·b, 0,25γb1·Rbt·b = 0,25·0,9·1,05·103·0,3 = 70,9 кН/м, 354 кН/м > 70,9 кН/м, условие выполняется, следовательно, поперечная арматура учитывается в расчете. Определяем длину проекции невыгоднейшего наклонного сечения: 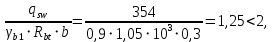 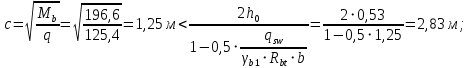 тогда 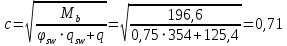 м, но не менее h0 и не более 3h0. м, но не менее h0 и не более 3h0.h0 = 0,53 м ≤ с ≤ 3h0 = 3·0,53 = 1,59 м. Принимаем c = 0,71 м. Длину проекции наклонной трещины c0 принимают равным c, но не менее h0 и не более 2h0. h0 = 0,53 м ≤ с ≤ 2h0 = 2·0,53 = 1,06 м. Принимаем c = c0 = 0,71 м. Поперечная сила, воспринимаемая поперечной арматурой: Qsw = φsw·qsw·c0 = 0,75·354·0,71 = 188,5 кН. Поперечная сила, воспринимаемая бетоном: 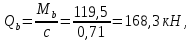 но не более Qb,max = 2,5γb1·Rbt·b·h0 = 2,5·0,9·1,05·103·0,3·0,53 = 375,4 кН, и не менее Qb,min = 0,5γb1·Rbt·b·h0 = 0,5·0,9·1,05·103·0,3·0,53 = 75,1 кН. Принимаем Qb = 168,3 кН. Проверяем условие Q1 = 306,6 кН > Qb + Qsw = 168,3 + 188,5 = 356,8 кН Окончательно устанавливаем в ригеле поперечную арматуру диаметром 10 мм класса А500С • на приопорных участках длиной ¼ l − у опоры А с шагом 250 мм; − у опор В и С с шагом 150 мм. • на средних участках − крайнего пролета с шагом 200 мм; − среднего пролета с шагом 200 мм. Для обеспечения прочности наклонных сечений на действие изгибающего момента необходимо всю продольную арматуру нижней зоны в крайнем пролете со стороны опоры А довести до конца ригеля или у нижнего ряда арматуры (3Ø25 мм) со стороны опоры А предусмотреть устройство на концах стержней специальных анкеров в виде пластин, шайб, гаек, уголков, высаженных головок и т. п. |
