Диплом транспортное предприятие. 120215 ДР транспорт ОТ МГ. 1. теоретическая часть 5 1 Теория разработки расписаний 5

• Название: 1. теоретическая часть 5 1 Теория разработки расписаний 5
• Анкор: Диплом транспортное предприятие
• Дата: 16.08.2022
• Размер: 3.45 Mb.
• Имя файла: 120215 ДР транспорт ОТ МГ.docx
• Тип: Реферат; #646821
• страница: 2 из 17

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1.1 Теория разработки расписаний

В 30-х годах 20-го века началось создание прогрессивного научного метода выработки коли­чественно обоснованных рекомендаций по принятию решений, получившего название «исследование операций» (ИО). Важ­ность количественного фактора в ИО и целенаправленность сформули­рованных рекомендаций позволяют определить ИО как теорию приня­тия оптимальных решений. ИО способствует превращению искусства принятия решений в математическую дисциплину.

Первоначально ИО было связано с решением задач военного содержа­ния, но уже с конца 40-х годов прошлого века оно используется для решения технических, технико-экономических задач, а также задач управления на различных уровнях.

Теория расписаний – это раздел исследования операций, в котором строятся и анализируются математические модели календарного планирования (т.е. упорядочивания во време­ни) различных целенаправленных действий с учетом целевой функции и различных ограничений.

Задачи составления расписаний возникают в частности:

• 
  на производстве, когда нужно упорядочить отдельные операции по исполнителям (цеха, станки) и по времени;
  
• 
  при планировании занятий в учебных заведениях;
  
• 
  при планировании занятости персонала, например, дежурства вра­чей;
  
• 
  при выполнении сложных продолжительных проектов строитель­ства зданий, кораблей и т.п.;
  
• 
  при планировании проведения спортивных мероприятий;
  
• 
  на транспорте при составлении расписания движения поездов, са­молетов, общественного городского транспорта.
  

Содержательно многие задачи ТР являются оптимизационными, т.е. состоят в выборе (нахождении) среди множества допустимых расписа­ний (расписаний, допускаемых условиями задачи) тех решений, на кото­рых достигается «оптимальное» значение целевой функции. Обычно под «оптимальностью» понимается минимальное или максимальное значение некоторой целевой функции. Допустимость расписания понимается в
13
смысле его осуществимости, а оптимальность — в смысле его целесо­образности.

Таким образом, для решения задач теории расписания необходимо построить математическую модель, т.е. описать с использованием математического аппа­рата изучаемые процесс или явление.

До 20-го века решение задач аналогичных задачам, решаемым средствами ТР не требовало много времени или боль­шого числа вычислений. В начале прошлого века развитие науки и тех­ники ускорилось. Увеличился темп и обыденной жизни. Задачи составле­ния расписаний оперировали все большим количество взаимосвязанных работ, и упорядочить их во времени становилось все труднее.

К началу 20-го века относятся два показательных примера. В период 1903 по 1919 гг. американский ученый Генри Гантт публикует ряд науч­ных работ и предлагает новый способ представления расписаний, полу­чивший название “Диаграмма Гантта”. Гантт занимался исследованием и улучшением руководства (менеджмента) на промышленных предприя­тиях (например, в компании по производству хлопчатобумажных тканей на предприятиях по постройке кораблей). Диаграмма Гантта – это схе­матичное изображение календарного плана. В ней работы представлены в виде прямоугольников, размещенных вдоль оси времени. Длина прямо­угольника соответствует времени, необходимому на выполнение соответ­ствующей работы. На диаграмме указаны как продолжительность рабо­ты так и время ее начала и окончания. На рисунке 1.1 приведен пример такой диаграммы для процесса написания диплома студентом.



Рисунок 1.1 - Диаграмма Гантта

К середине 20-го века выделились еще две области знаний, некоторые задачи которых впоследствии стали частью ТР . Это сетевое планиро­вание и теория массового обслуживания.

Сетевое планирование – совокупность методов анализа, пла­нирования и управления, использующих сетевую модель как основную форму представления информации об управляемом комплексе работ.

Сетевая модель – информационно-аналитическая модель ре­ализации некоторого комплекса взаимосвязанных работ, рас­сматриваемая как ориентированный граф без контуров, отоб­ражающий естественный порядок выполнения этих работ во времени.

Сетевая модель может содержать некоторые другие характеристики (например, время, стоимость, ресурсы), относящиеся к отдельным рабо­там или комплексу в целом.

Использование сетевого планирования позволяет повысить качество планирования и управления при реализации комплекса работ. Напри­мер, дает возможность четко координировать деятельность всех сторон (исполнителей), участвующих в реализации, выделять наиболее важные задачи, определять сроки реализации и т.д.

Методы сетевого планирования являются основой специальных ком­пьютерных программ – систем сетевого планирования и управления, та­ких как Microsoft Project, Oracle Primavera и т.д.

На рисунке 1.2 представлен пример сетевого графика соответствующего диаграмме Гантта на рисунке 1.1.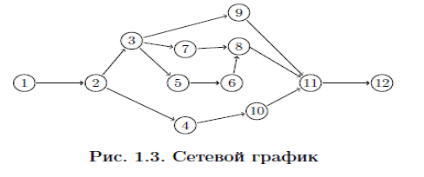


Рисунок 1.2 - Сетевой график

Итак, в первой половине 20-го века был сформулирован ряд практи­ческих и теоретических задач составления расписаний. В 1956-м году Ричард Беллман предложил термин «Теория расписаний» для обо­значения совокупности данных задач и относящихся к ним научных зна­ний. В 1967-м году публикуется монография Конвея, Максвелла и Мил­лера «Теория расписаний». В 1975-м году перевод этой книги на рус­ский язык синхронно выходит с книгой советских авторов В.С. Танаева В.В. Шкурбы «Введение в теорию расписаний». С этих пор можно счи­тать ТР сформировавшейся теорией.


22
Рассмотрим основные способы представления расписаний:

-табличное представление; в таблице представлены промежутки времени, в которые выполняются задания, а также их исполнители;

- графическое представление, например, с помощью Диаграммы Гантта;

- Для некоторых задач ТР возможно векторное (перестановоч­ное) представление расписания. При этом указывается лишь по­рядок выполнения заданий, например (2, 3, 4, 1).

По типу целевой функции задачи теории расписаний подразделяются на:

• 
  задачи с суммарными критериями оптимизации, когда, например, необходи­мо минимизировать суммарное значение моментов окончания обслуживания;
  
• 
  задачи с minmax (минимаксными) критериями оптимизации, отличие которых от задач с суммарными критериями заклю­чается в том, что нужно минимизировать не сумму некоторых значений, а лишь максимальное из них.
  
• 
  многокритериальные задачи оптимизации, когда в исследуе­мой задаче необходимо построить оптимальное решение с точ­ки зрения нескольких целевых установок (функций);
  
• 
  задачи на построение допустимого расписания. Необходимо отметить, что данный класс задач можно свести к оптимизационным за­дачам, введя специальную функцию штрафа, который нужно минимизировать. Тем не менее, принято выделять такие задачи в отдельный класс.
  

В рамках ТР принято выделять следующие разделы:

• 
  Сетевое планирование или построение расписания для проекта, Project scheduling (PS);
  
• 
  Календарное планирование или построение расписания для приборов, Machine scheduling (MS);
  
• 
  Составление временных таблиц (Time TaЫing);
  
• 
  Доставка товаров в магазины (Shop-Floor Scheduling);
  
• 
  Составление расписаний движения транспортных средств (Transport Scheduling).
  

Приведенные классификации задач ТР условны и лишь указывают на некоторые характерные особенности решаемых задач.

Существенное место в ТР занимает такой раздел как «Составление временных таблиц (Time TaЫing)», отражающий составление графиков в различных сферах деятельности.

Задачи управления транспортными системами составляют важный класс задач управления транспортными системами. Этот класс можно описать в терминах сети, состоящей из точек (узлов), соединенных пу­тями (дугами), по которым осуществляются различные виды перевозок (потоки).

Задачи планирования транспортных перевозок восходят сво­ими корнями к работам французского математика Гаспара Монжа. Cущественное продвижению в этом направлении было получено совет­ским математиком и экономистом Леонидом Витальевичем Канторови­чем, вследствие чего непрерывная классическая постановка транс­портной задачи получила название задачи Монжа–Канторовича.

Рассмотрим дискретный вариант этой задачи — транспортную задачу линейного программирования.

Имеется m пунктов отправления A1, ... , A_m, в которых сосредоточе­ны запасы однородных продуктов в количестве a1, ... , a_m единиц.

Имеется n пунктов назначения B1, ... , B_m, потребность которых в указанных продуктах составляет b1, ... , b_n единиц.

Известны cij, i = 1, 2, ... , m; j = 1, 2, ... , n — стоимости перевозки единиц груза от каждого i-го поставщика каждому j-му потребителю. Требуется составить план перевозок, при котором все продукты достав­лены в пункты назначения, и суммарные затраты на перевозку всех гру­зов являются минимальными.

Выберем в качестве переменных xij, i = 1, 2,... , m, j = 1, 2, ... , n, объемы перевозок от i-го поставщика каждому j-му потребителю.

По условию задачи требуется обеспечить минимум суммарных затрат на перевозки. Следовательно, целевая функция задачи имеет вид: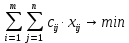
(1.1)
Суммарное количество груза, направляемого из каждого пункта отправ­ления во все пункты назначения, должно быть равно запасу груза в данном пункте: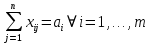
(1.2)
Вторая группа уравнений выражает требование удовлетворить запросы всех n потребителей полностью и имеет вид: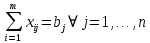
(1.3)
Объемы перевозок — неотрицательные числа: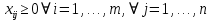
(1.4)
Как одна из задач линейного программирования, транспортная за­дача (1.1)–(1.4) может быть решена некоторым стандартным методом решения задач линейного программирования, кроме того, разработаны специальные методы, учитывающие специфику ограничений задачи.

Необходимо отметить, что задача в такой постановке не учитывает многих факторов, возникающих на практике. Перечислим некоторые из них.

- Неоднородность доставляемых грузов. Как правило, из раз­ных пунктов необходимо доставить различные виды грузов. Часто груз заранее определяется пунктом назначения.

- Ограничения на пропускную способность транспортыхсетей. Данные ограничения определяют возможность перемещения транспорта и зависят от вида путей (железнодорожные, водные, автомобильные пути).

- Ограничения на транспортные средства. Здесь могут быть учтены как количество транспортных единиц, имеющихся в нали­чии, так и ограничения на их эксплутационные свойства (грузоём­кость, скорость движения и т.д.).
40
Транспортные расходы могут включать в себя расход на горю­чее, ремонтные, эксплуатационные работы, привлечение обслужива­ющего персонала.

- Учет времени. Зачастую необходимо не только минимизировать издержки, но и время выполнения заказов. Также необходимо учесть директивные сроки, к которым должны быть доставлены то­вары.

В силу перечисленных ограничений необходимым оказывается не только определение, из какого пункта в какой будет доставляться груз, но и построение маршрутов перемещения товаров, а также расписания движения транспорта. Последнее из перечисленных ограничений наибо­лее сильно указывает на связь транспортных задач с теорией расписаний.

Очевидно, что задачи транспортного планирования могут сильно раз­личаться между собой в зависимости от вида транспортных систем. Задачи с жёсткими ограничениями на пропускную способность путей и транспортные средства характерны прежде всего для железнодорожного транспорта. Однако подобные ограничения могут возникать и применительно к другому транспорту, в том числе и речному.