ЖБК. 1. виды и особенности конструкций, и расчета стыков жб колонн стыки многоэтажных сборных рам

• Название: 1. виды и особенности конструкций, и расчета стыков жб колонн стыки многоэтажных сборных рам
• Анкор: ЖБК.doc
• Дата: 02.04.2018
• Размер: 5.41 Mb.
• Имя файла: ЖБК.doc
• Тип: Документы; #17513
• страница: 7 из 8

28. ОСОБЕННОСТИ РАСЧЕТА И КОНСТРУИРОВАНИЯ ГИПЕРБОЛИЧЕСКИХ ПАНЕЛЕЙ-ОБОЛОЧЕК

Они применяются двух разновидно­стей: в одном случае — сторонам контура основания параллельны линии главных кривизн поверхности (рис. XIV.25, а); в другом — линии главных кривизн поверхно­сти направлены вдоль диагоналей основания (рис. XIV.25,6).

Оболочки первой разновидности можно рассматри­вать как оболочки с поверхностями переноса. При этом следует учесть, что, поскольку кривизна поверхности в направле­нии оси ох отрицательна, усилия Nx будут растягиваю­щими. В направлении положительной кривизны сохранится сжатие. Растягивающие усилия Nx должны быть полностью восприняты рабочей арматурой, которую сле­дует предварительно напрягать.

Поверхность оболочки второй разновидности описы­вается уравнением



Ее кривизны



Уравнение равновесия (XIV.1) в данном случае упро­щается



Рассмотрим оболочку, нагруженную равномерно рас­пределенной нагрузкой q. Функция напряжений



Она удовлетворяет граничным условиям: N_x = 0 при х= = ±а и N_y=0 при у= ± b(вследствие полной гибкости контурных конструкций из своей плоскости), а также уравнению равновесия (XIV.44).

Согласно зависимостям (XIV.2):



Таким образом, N_x и N_y равны нулю не только на гра­ницах Оболочки, но и во всей ее области; касательные же усилия N_xy постоянны по значению, имеют направление, обратное указанному на элементе оболочки (рис. XIV.25,6). В целом оболочка находится в условиях чис­того сдвига.

В практике удобнее других поверхности при a=b, равносторонние гиперболические параболоиды. В этом случае главные усилия (вдоль линий главных кривизн) и их направления, определенные по формулам



Следовательно, в направлении линии главной отрица­тельной кривизны развиваются растягивающие усилия постоянного значения. По направлению линии главной положительной кривизны действуют сжимающие усилия.

Главные растягивающие усилия должны быть пол­ностью восприняты рабочей арматурой одного диагонального в плане направления (криволинейной) или двух на­правлений вдоль сторон контура (прямолинейной), как показано на рис. XIV.25, б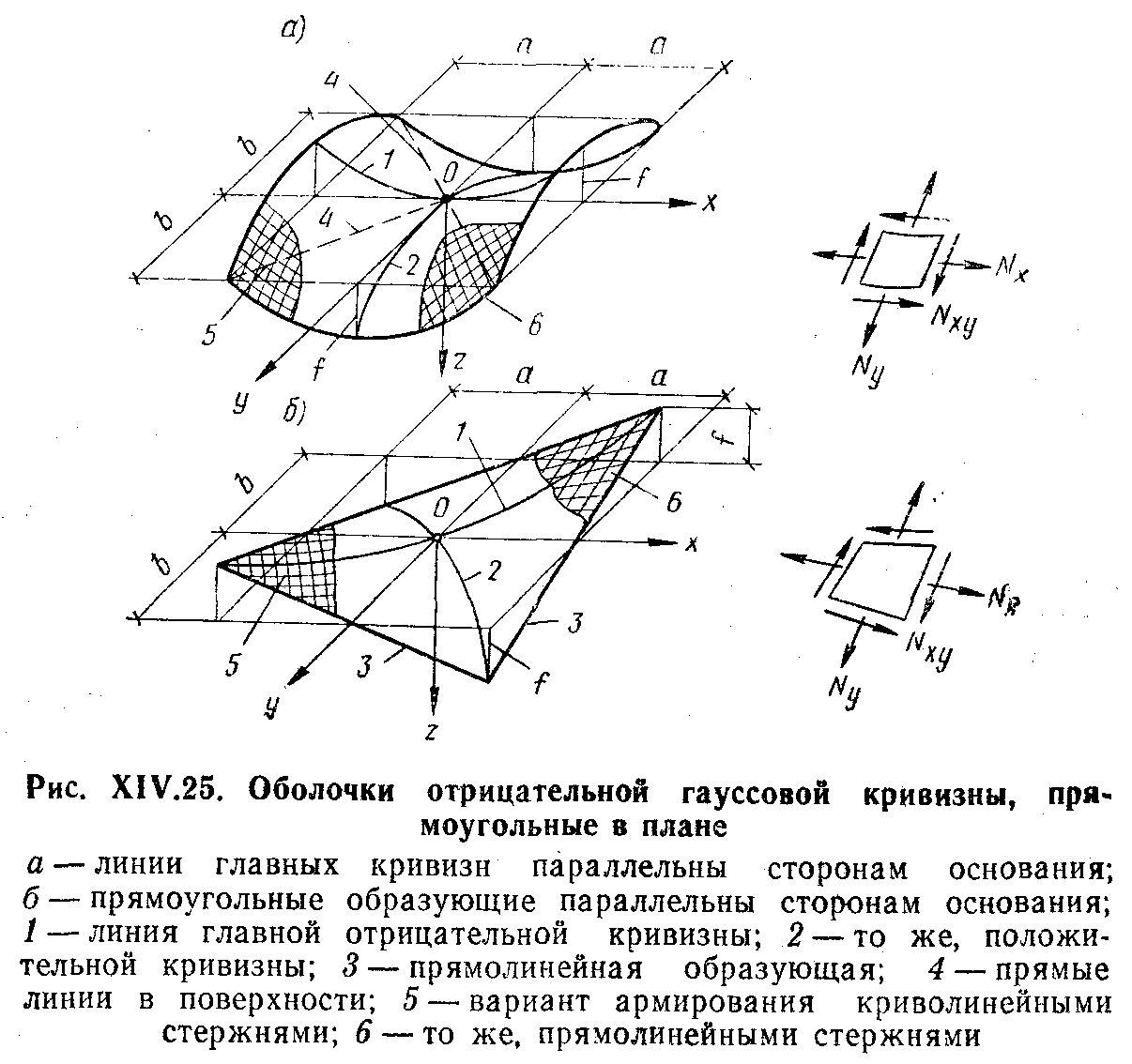



29. ОСОБЕННОСТИ РАСЧЕТА И КОНСТРУИРОВАНИЯ КУПОЛОВ

Ку­польное покрытие состоит из двух основных конструктив­ных элементов: оболочки и опорного кольца (см. рис. XIV.1,0; XIV.27, а).

Купол с непрерывным по контуру шарнирно-подвижным опиранием, совпадающим по направлению с каса­тельной к оболочке, является статически определимой конструкцией (рис. XIV.27,а). Тонкостенные купола по­добно другим пространственным покрытиям можно рас­считывать по безмоментной теории.

Элемент купола, ограниченный двумя меридиональ­ными и двумя кольцевыми сечениями, находится под воз­действием усилий: меридионального, кольцевого и касательного N_I, N₂, S (рис. XIV.27, в), отнесенных к единице длины сечения. При осесимметричной нагрузке S = 0. Введем обозначения:Ψ— текущая угловая координа­та; Q — нагрузка на сегмент, ограниченный углом Ψ.

Из условия равновесия элемента купола (рис. XIV.27,e) найдем





Рассмотрим купол с шаровой поверхностью при R₁= R₂ = R. Обозначим нагрузку от собственного веса ша­рового купола на единицу поверхности g; тогда (рис. XIV.28.C)



Используя формулы (XIV.51) и зависимости



из выражений (XIV.48) и (XIV.50) находим



Для полушарового купола эпюры N₁ и N₂ изображены на рис. XIV.28, б, в. Отметим, что при Ψ=0 имеем N₁₌=Rg/2 (сжатие) u.N₂=Rg/2 (сжатие): при Ψ=π/2 име­ем N₁=Rg (сжатие) и N₂=—Rg (растяжение).

Кольцевое сечение, в котором N₂=0—шов перехода, определяется углом ф = 51°49'.

Аналогично получаем решение для шарового купола при снеговой нагрузке p, которая считается равномерно распределенной по горизонтальной проекции и меняю­щейся по поверхности купола пропорционально cos Ψ: N₁=0,5pR (постоянное значение вдоль меридиана);



Основные нагрузки, определяющие размеры конст­рукций купола,— собственный вес оболочки вместе с утеплителем и кровлей, а также снеговая нагрузка. Обе нагрузки принимают действующими осесимметрично. Ветровые нагрузки при пологих купольных покрытиях решающего значения, не имеют и могут не приниматься во внимание. При высоких куполах, встречающихся ре­же, усилия от ветровых нагрузок определяют приемами, изложенными в теории упругости.

В реальных конструкциях оболочка купола оперта не свободно, а имеет упругое закрепление в опорном коль­це (рис. XIV.29,а). В связи с этим на опорном контуре оболочки возникают дополнительные статически неопре­делимые величины — изгибающий момент М₀, действу­ющий в меридиональном направлении, и радиальный распор Н₀ (рис. XIV.29,б). Их определяют из условия совместности деформаций оболочки и опорного кольца. Влияние упругого контурного закрепления сказывается на оболочке лишь вблизи кольца и накладывается на общее ее безмоментное напряженное состояние.

В зоне местного изгиба справедливо уравнение (XIV.23). Его решение относительно момента представ­ляется выражением (XIV.24), а относительно перемеще­ний w, нормальных к поверхности оболочки, выражением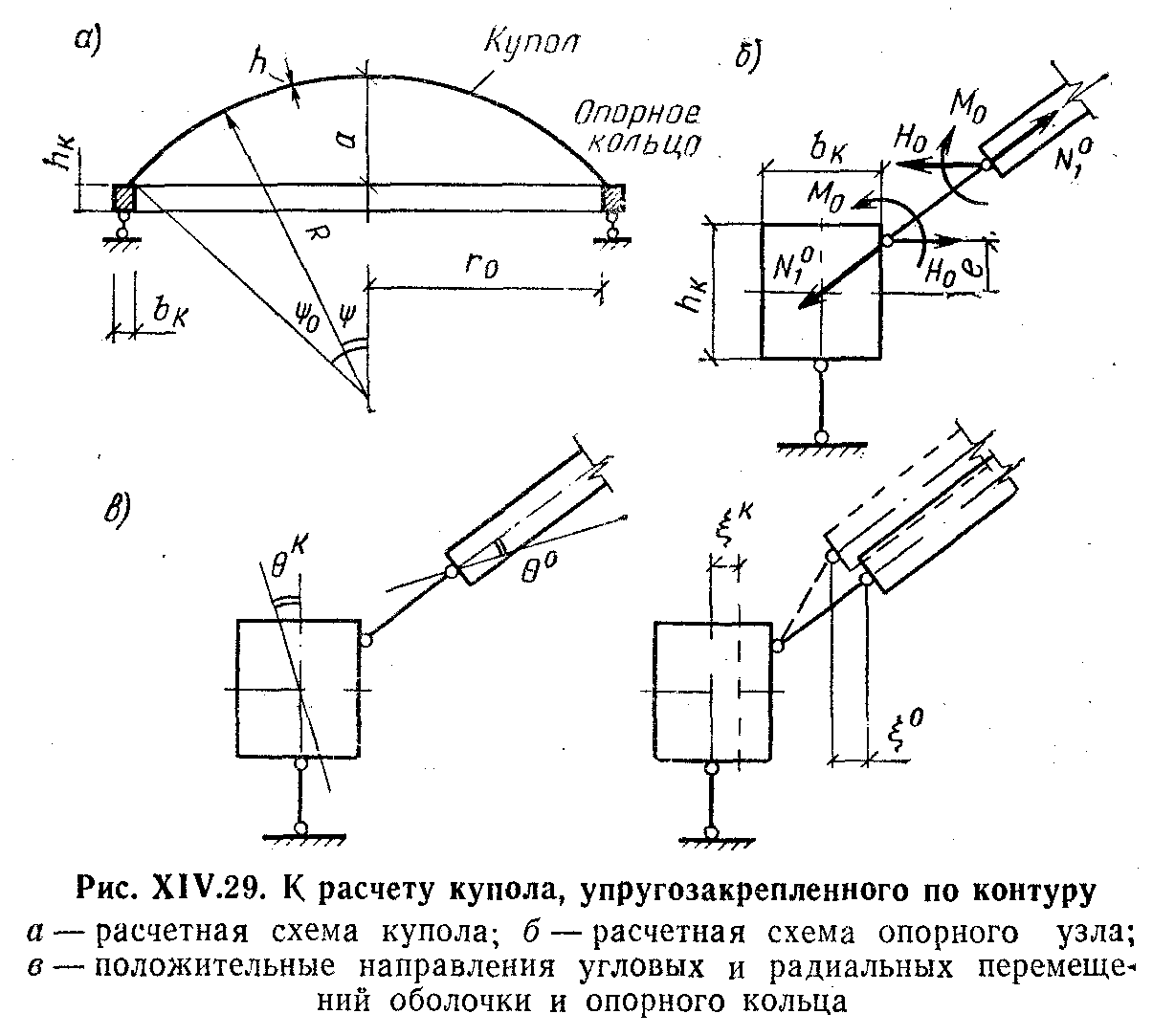













От воздействия распора H₀ на опорное кольцо (рис. XIV.30, а) в нем возникает растягивающее усилие N^K_H ,которое вызывает радиальное перемещение оси кольца ξ ^K_H. Распор H₀ приложен к кольцу с эксцентриситетом e (рис. XIV.29,б), образуя момент H₀e, отчего кольцо по­ворачивается на угол. θ^K_H.

От воздействия момента М₀, равномерно распреде­ленного вдоль кольца, его поперечные сечения поворачи­ваются на один и тот же угол θ^K_M., (рис. XIV.30,б). При этом слой кольца на уровне центра тяжести его сечения не деформируется; часть сечения, расположенная выше, испытывает растяжение, а расположенная ниже,— сжа­тие. Кольцо в целом испытывает изгиб в осевом верти­кальном направлении.

Угловые суммарные перемещения края оболочки и опорного кольца по линии их контакта, вызванные на­грузкой и неизвестными М₀ и Н₀, должны быть равны:



То же относится и к радиальным перемещениям:



Изгибающие моменты в зоне местного изгиба опре­деляют по выражению (XIV.24), которое после преобра­зований принимает вид



Кольцевое усилие слагается из воздействий нагрузки, М₀ и H₀:



В опорном кольце действуют осевое усилие N и из­гибающий момент М:



Опорное кольцо находится в условиях внецентренного растяжения. Вследствие малости изгибающего момента его можно рассчитывать как центрально-растянутое.

В сборных куполах, если примыкание оболочки к опорному кольцу конструируется как безмоментное, мо­мент М₀ должен быть принят равным нулю.

Устойчивость гладких оболочек купола считается га­рантированной, если интенсивность полной расчетной на­грузки не превышает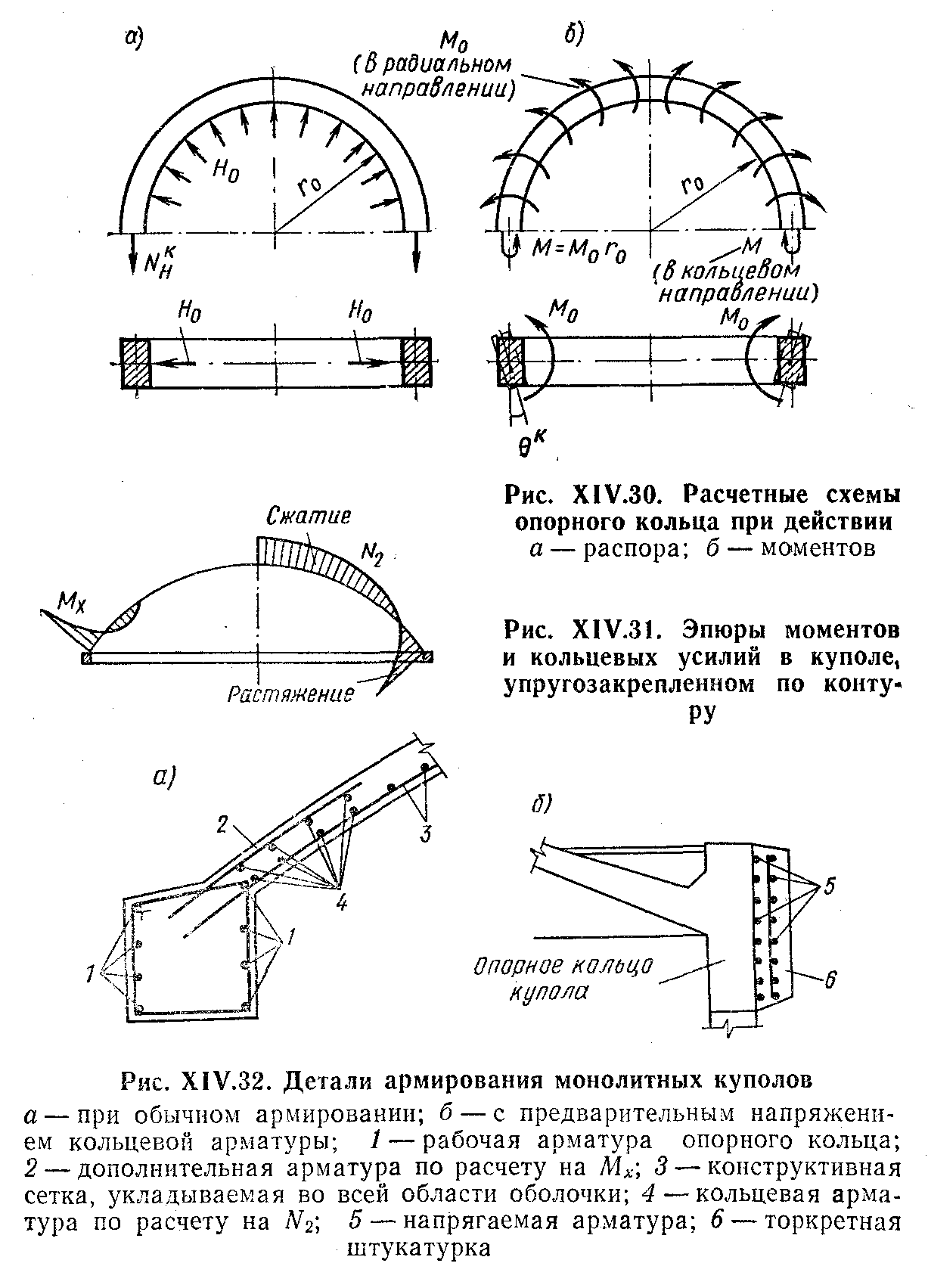





Монолитные купола делают преимущественно гладки­ми. Оболочки пологих куполов, за исключением приопорных зон, сжаты; их армируют конструктивно — одиноч­ной сеткой из стержней d=5...6 мм с шагом 15—20 см. У контура ставят дополнительную меридиональную ар­матуру, рассчитанную по опорному моменту Мх, обычно из стержней d = 6...8 мм, и дополнительную кольцевую арматуру для восприятия местных растягивающих коль­цевых усилий N2 (рис. XIV.32,а). Рабочую арматуру опорного кольца ставят в виде кольцевых стержней d = =20...30 мм, которые по длине соединяют при помощи сварки.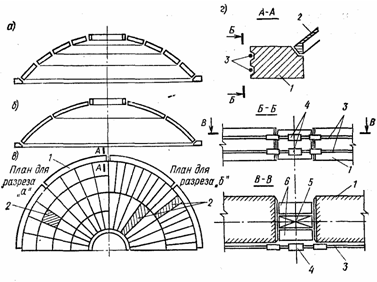



30. КОНСТРУКТИВНЫЕ СХЕМЫ КАМЕННЫХ ЗДАНИЙ И ОСОБЕННОСТИ ИХ РАСЧЕТА

В зависимости от конструктивной схемы здания каменные стены делятся на: несущие, воспринимающие кроме нагрузок от собственного веса нагрузки от покрытий, перекрытий, кранов и т. п.; самонесущие, воспринимающие нагрузку толь­ко от собственного веса стен всех этажей здания и ветровую на­грузку; ненесущие (в том числе навесные), воспринимающие только нагрузку от собственного веса и ветра в пределах одного этажа или одной панели каркасных зданий при высоте этажа не более 6 м; при большей высоте этажа стены этого типа отно­сятся к самонесущим.

По степени пространственной жесткости различа­ют здания с жесткой конструктивной схемой и здания с упругой конструктивной схемой.

Конструктивная схема определяется расстоянием l_ст между поперечными вертикальными устойчивыми конструкциями и жесткостью (неподвижностью) горизонтальных опор.

К зданиям с жесткой конструктивной схемой относятся в большинстве случаев гражданские здания, в которых при расчете на горизонтальные нагрузки, внецентренное и центральное сжа­тие несущие каменные стены и столбы рассчитывают как верти­кальные балки, опирающиеся в горизонтальном направлении на жесткие опоры (покрытия и междуэтажные перекрытия) при расстоянии между поперечными устойчивыми конструкциями.

Жесткими (неподвижными) горизонтальными опорами могут служить пояса, фермы, связи и железобетонные обвязки, рассчи­танные по прочности и по деформациям на восприятие горизон­тальной (ветровой) нагрузки, передающейся от стен.

Жесткими вертикальными опорами являются поперечные устойчивые конструкции (каменные и бетонные стены толщиной не менее 12 см, железобетонные — толщиной не менее 6 см, контрфорсы, поперечные рамы с жесткими узлами и другие кон­струкции, рассчитанные на восприятие горизонтальной нагрузки от примыкающих к ним стен).



Расчет на внецентренное сжатие и изгиб из плоскости. В зда­ниях с жесткой конструктивной схемой стены и столбы рассчиты­вают на вертикальные и горизонтальные ветровые нагрузки с учетом их возможного сочетания как вертикальные неразрезные многопролетные балки, опертые на неподвижные опоры — пере­крытия (рис. 72, а). Нагрузки в пределах рассматриваемого этажа считаются приложенными с фактическими эксцентрисите­тами относительно центра тяжести сечения стены или столба с учетом изменения сечения стены в пределах этажа и ослабления горизонтальными и наклонными бороздами.

Изгибающие моменты учитываются от вертикальных и гори­зонтальных (ветровых) нагрузок, приложенных в пределах рас­сматриваемого этажа, а также от вертикальных нагрузок выше­расположенных этажей, если сечение стены изменяется в уровне перекрытий над данным этажом или в пределах рассчитываемого этажа.

Основные расчетные формулы для определения в сечении стен (столбов) нормальных сил и изгибающих моментов при при­нятой (рис. 72, б) расчетной схеме от вертикальных нагрузок приведены в табл.20.

Изгибающие моменты в сечении наружной стены от горизон­тальной ветровой нагрузки (рис. 72, в) определяются в пределах каждого этажа (за исключением верхнего) как для балки с заде­ланными концами по формуле

M=±qH²_эт/12, (1)

где q — ветровая равномерно распределенная в пределах рас­сматриваемого этажа нагрузка, приходящаяся на 1 м высоты стены; Hэт — высота этажа (пролет балки). Для верхнего этажа верхнюю опору балки считают шарнирной.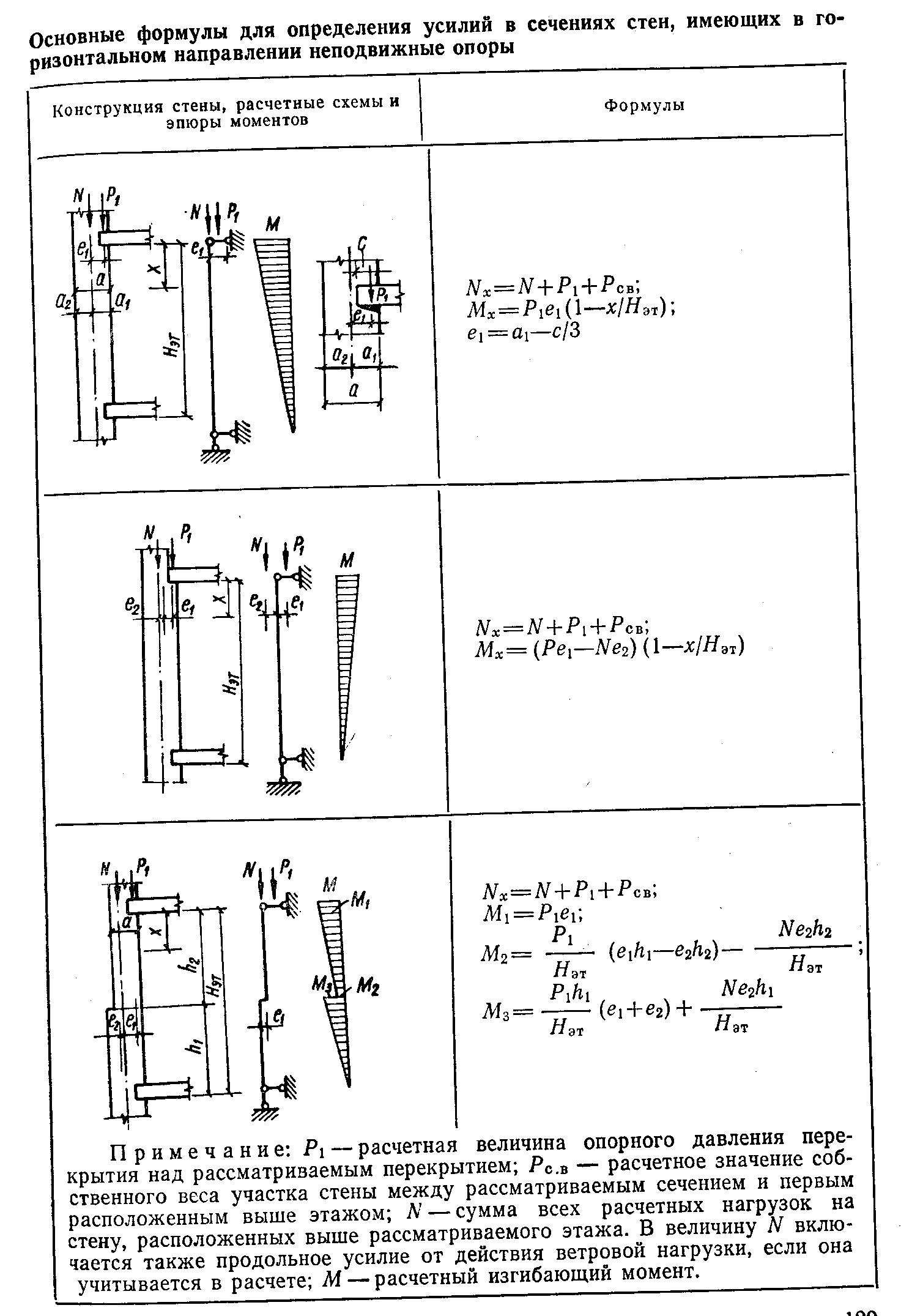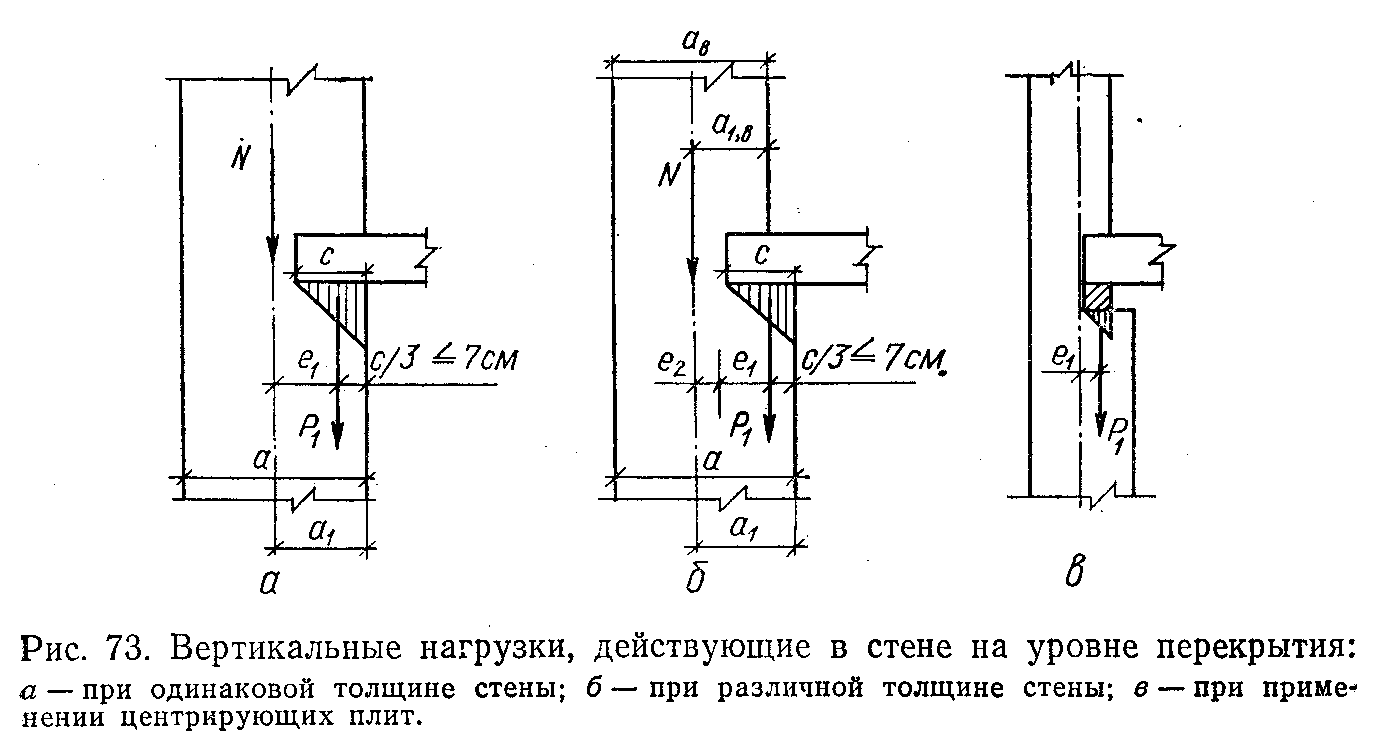





Расчет стен или столбов обычно начинают с верхнего этажа. При определении усилий, действующих на стену в пределах рас­сматриваемого этажа, учитывают: расчетное опорное давление перекрытия над рассматриваемым этажом Р₁, приложенное в уровне низа этого перекрытия с эксцентриситетом е₁ относитель­но центра тяжести сечения стены; сумму всех расчетных нагру­зок N на стену, расположенных выше рассматриваемого этажа, с включением продольного усилия от действия ветровой нагруз­ки (если она учитывается в расчете), приложенную в уровне ни­за перекрытия над рассматриваемым этажом с эксцентриситетом е₂ относительно центра тяжести сечения стены; расчетный соб­ственный вес участка стены между рассматриваемым сечением и первым расположенным выше этажом Рс.в, приложенный в цен­тре тяжести этого участка стены (см. рис. 73 и табл. 20).

Изгибающие моменты М в рассчитываемых сечениях стены изменяются от максимального значения на уровне низа верхнего перекрытия до нуля на уровне низа нижнего перекрытия и опре­деляются по принятой статической схеме (рис. 72, б).

Несущая способность стены в пределах этажа должна опре­деляться для сечения под балкой (прогоном) верхнего перекры­тия, где изгибающий момент обычно наибольший, а влияние про­дольного изгиба не сказывается — в этом сечении, как опорном, коэффициент продольного изгиба равен 1.

При статическом расчете каменных стен и столбов зданий с упругой конструктивной схемой выделяют один ряд поперечных конструкций между средними осями пролетов зданий и рассмат­ривают рамную систему. Стойками рамы являются стены и стол­бы, которые принимаются заделанными в грунт в уровне пола здания (при наличии бетонного подстилающего слоя под полы и отмостки), а конструкция покрытия (ферма, прогон) —ригелем, шарнирно связанным со стойками (рис. 77).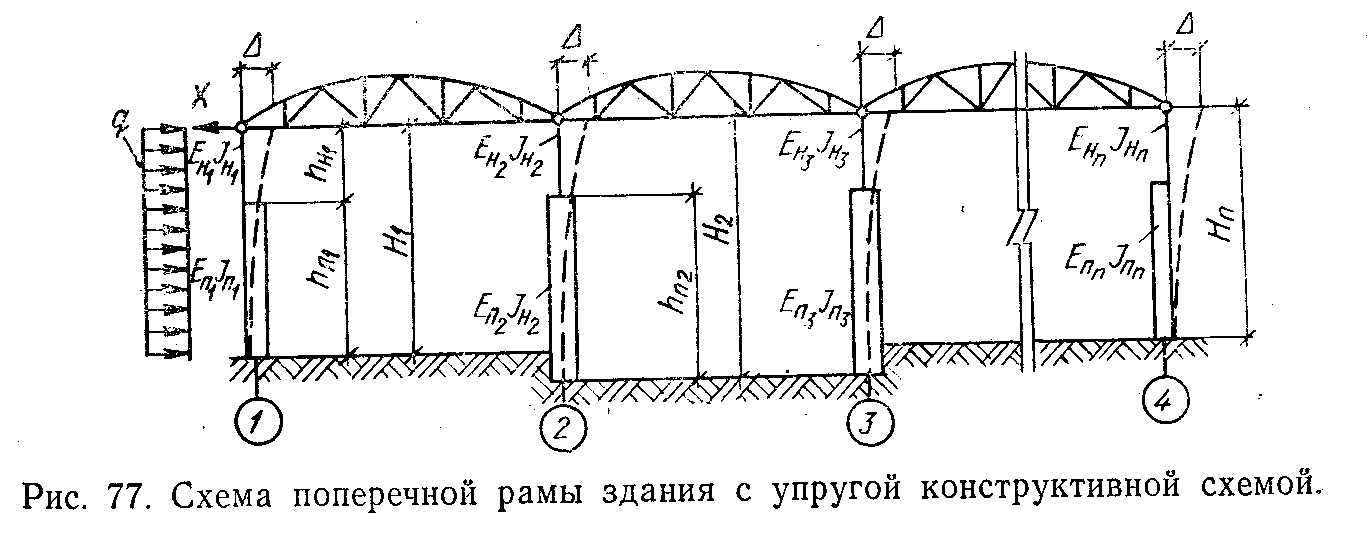



Стены и столбы зданий с упругой конструктивной схемой рас­считывают с учетом разных условий их работы, соответствующих двум стадиям готовности здания.

В первой стадии, когда стены и столбы возведены, а перекрытия или покрытия еще не установлены, расчет выполня­ется с целью определения необходимости установки временных креплений, чтобы не увеличивать сечений стен и столбов сверх требуемых для законченного здания. При этом изгибающие мо­менты М и продольные силы N в опасных сечениях определяют, как для консольных стоек, заделанных в грунт, на которые дей­ствуют собственный вес, ветровые нагрузки, вес некоторых видов -оборудования (рис. 78,a).

Опасными сечениями обычно являются верхние и нижние се­чения каждой ступени стойки сечения (/—/, //—//, ///—/// стен, конструкция которых показана на рис. 78, а). При действии соб­ственного веса и равномерно распределенной ветровой нагрузки изгибающие моменты и продольные силы в опасных сечениях определяются по формулам:

в сечениях I—I и //—//

N_I-I=N_II-II=Q_н;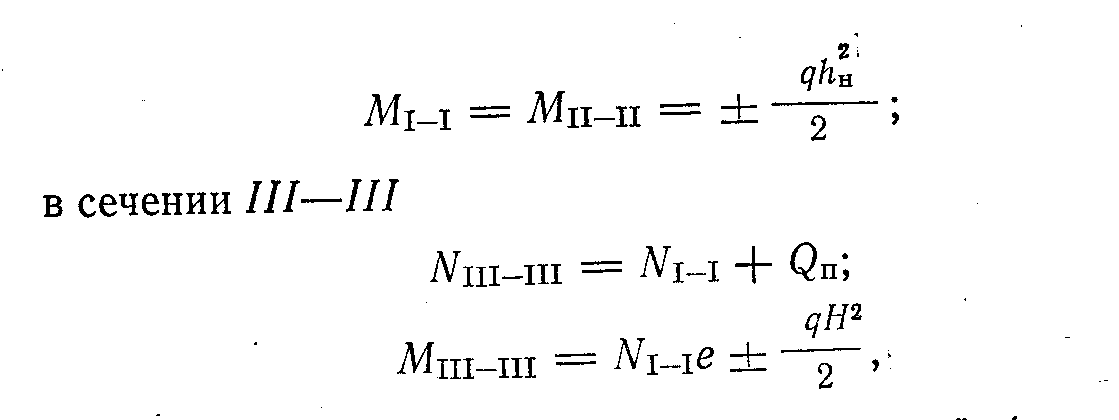



где Q_H и Q_П — соответственно вес надкрановой (выше сечения II—II) и подкрановой (между сечениями Ш—/// и //—//) части стены; h3 и Н — соответственно высота надкрановой части стены и всей стены; е — расстояние между центрами тяжести верхнего и нижнего сечений стойки; q — ветровая нагрузка (напор или от­сос) на 1 погонный метр стоек поперечной рамы, собранная с ши­рины стены, равной шагу поперечных конструкций.

Ветровую нагрузку q принимают равномерно распределенной для стоек высотой до 10 м.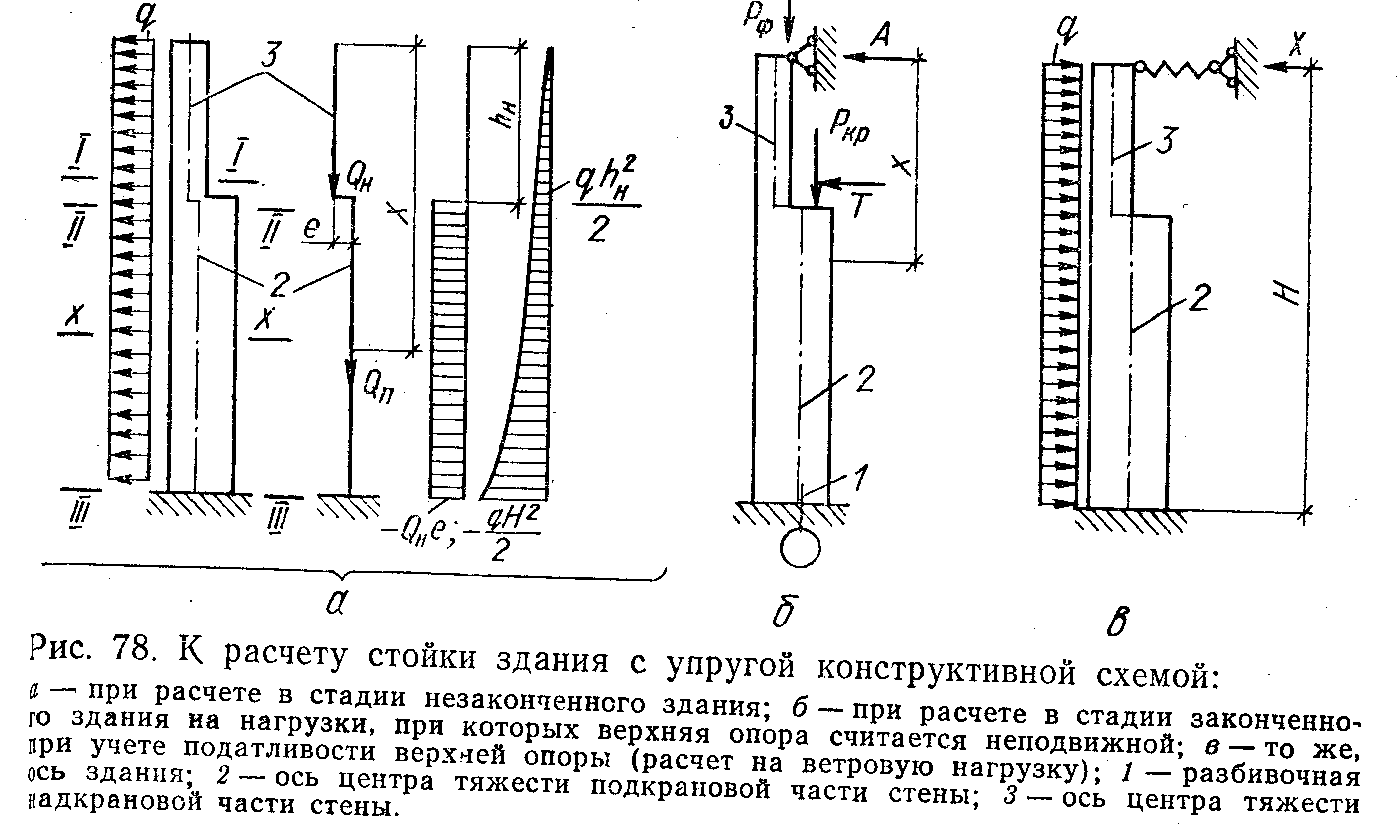



Подсчитав для каждого сечения продольную силу и изгибаю­щий момент от всех нагрузок, определяют суммарные усилия М и N, опасные для прочности рассматриваемого сечения, т. е. со­ставляют основные или особые сочетания следующих усилий:

1) наибольший положительный момент Ммакс и соответствую­щее ему продольное усилие N_COOТ;

2) наибольший отрицательный момент М_Мин и соответствую­щее ему значение N_Cooт,

3)наибольшая нормальная сила N_макс и соответствующее ей значение М_СООт.

Получив в сечении момент и соответствующую этому моменту нормальную силу в зависимости от эксцентриситета е₀, проверя­ют его несущую способность, учитывая длительное действие на­грузки.