2. Приближение функций Задача приближения функций
 Скачать 7.11 Mb.
|
2.10. Интерполяционный многочлен Ньютона с конечными разностямиЕсли интерполируемая функция задана на таблице с постоянным шагом  , то можно использовать связь между конечными и разделенными разностями:  В этом случае многочлен Ньютона можно записать несколько в ином виде:Пусть   Преобразуем разделенные разности в конечные:  тогда   и так далее.Тогда многочлен Ньютона можно переписать в следующем виде:  (2.10.1)Эту формулу называют интерполяционным многочленом Ньютона с конечными разностями для интерполяции вперед. В ней используются только конечные разности, расположенные в верхней косой строке таблицы конечных разностей. Если использовать разности нижней косой строки, то аналогично получим многочлен Ньютона с конечными разностями для интерполяции назад: 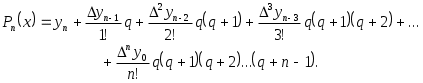 (2.10.2)Пример. Вычислить  в точках  , используя формулы (2.10.1) и (2.10.2) при  , если
Здесь 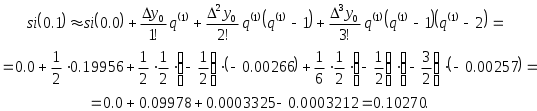 Для 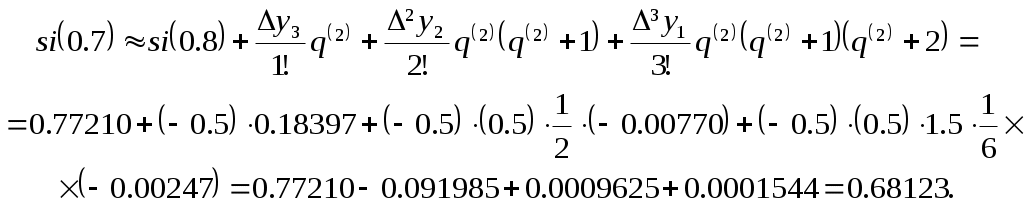 используем формулу (2.10.1), так как значение  расположено в начале таблицы, тогда   Для  лучше использовать формулу (2.10.2), так как расположено ближе к нижнему краю таблицы. Тогда   |
