2. Приближение функций Задача приближения функций
 Скачать 7.11 Mb.
|
2.9. Лабораторная работа № 2. Интерполирование и экстраполирование данных. Интерполяционный многочлен ЛагранжаВ практических расчетах чаще всего используют интерполяционные многочлены невысоких степеней. Из формулы (2.3.4) видно, что единственный, восстанавливаемый без дополнительных условий многочлен Лагранжа должен иметь степень, на единицу меньшую числа точек интерполяционной таблицы. Обычно по исходным данным именно такой многочлен и восстанавливается. По найденному многочлену находят приближенные значения функции для любых значений аргумента, лежащих между узлами заданной сетки. Пример. Найти многочлен наименьшей степени, принимающий в данных точках заданные значения:
Здесь заданы лишь три узла сетки. Следовательно, можно восстановить многочлен Лагранжа второго порядка: 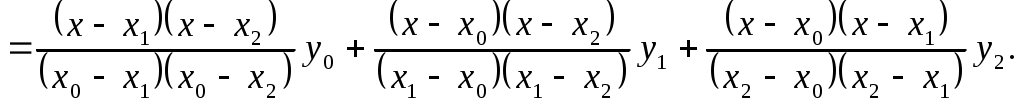  Вычислим вначале коэффициенты       Тогда     Для вычисления лагранжевых коэффициентов  удобно применить следующую таблицу разностей (2.9.1):
на главной диагонали которой стоят разности вида  Если обозначить произведение элементов  -й строки через  , а произведение элементов главной диагонали через  , то  (2.9.2)Для рассмотренного выше примера таблица разностей будет иметь вид Тогда, например, для 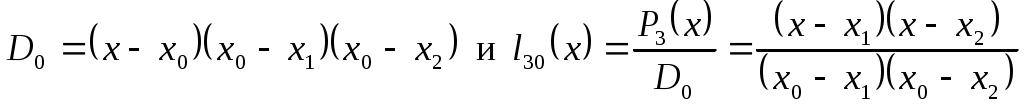 получим   , что совпадает с выражением, найденным по формуле (2.3.4).Теперь по найденному интерполяционному многочлену Лагранжа можно посчитать приближенное значение функции  для любого значения аргумента  . Вычислим, например,   Результат необходимо округлить до второго знака после запятой. Итак,  Если требуется найти не общее выражение  , а лишь его значения при конкретных значениях аргумента, то удобно пользоваться интерполяционной схемой Эйткена по формулам (2.8.1) и (2.8.2). Вычислим еще раз  , расположив данные по схеме Эйткена в удобной таблице (2.9.3):
Вычисления по схеме Эйткена обычно ведут до тех пор, пока последовательные значения  и  не совпадут в пределах заданной точности.В нашем случае из-за малого количества узлов таблица получилась очень короткой, содержащей всего три многочлена:  ,  и  . Вычислим их:   
Итак,  Приведенный пример показывает, что значение таблично заданной функции в точке лучше вычислять по схеме Эйткена, что обеспечивает большую точность при меньших вычислительных затратах. При определении лагранжевых коэффициентов возможна потеря точности из-за малых знаменателей соответствующих дробей, кроме того восстановленный  имеет большие и противоположные по знаку коэффициенты, что также требует сохранения лишних знаков в промежуточных вычислениях. |
