2. Приближение функций Задача приближения функций
 Скачать 7.11 Mb.
|
|
Задание № 2. Используя схему Эйткена, вычислить приближенное значение функции  , заданной таблично при данном значении аргумента  .I.
II.
III.
IV.
V.
В ыполним теперь те же действия в пакете Мathcad, освоив простейшие символьные вычисления, панель программирования, а также действия с векторами и матрицами. Рассмотрим и решим две задачи, аналогичные заданиям № 1 и № 2: построим многочлен Лагранжа по заданной таблице и вычислим приближенное значение функции по схеме Эйткена. Для выполнения обеих этих задач удобно воспользоваться аппаратом матричной алгебры пакета. К  нопка -Vector and Matrix Palette (Панель векторных и матричных опе-раций) открывает панель, изображенную чуть ниже, кнопки которой соответствуют следующим операциям: - определение размеров матрицы; - численное вычисление определителя матрицы; - поэлементные операции с матрицами (режим векторизации); - скалярное произведение двух векторов; - векторное произведение; - вычисление суммы компонент вектора  ;- определение столбца матрицы:  -й столбец матрицы;- транспонирование матрицы; - визуализация цифровой информации, сохраненной в матрице. Три действия: транспонирование, обращение матрицы и вычисление определите- ля - можно выполнить и из меню символьных операций (Symbolics). Имеется три способа создания векторов и матриц в пакете Mathcad: заполнением массива пустых полей, предварительно созданной матрицы нужной размерности с помощью панели определения размеров; использованием дискретного аргумента, чтобы определить элементы матрицы; считыванием матрицы из файлов данных. Итак, рассмотрим первую задачу. Пусть функция задана таблицей
В ведем исходные данные и матрицу, соответствующую таблице (2.9.1). Для того чтобы определить вектор или матрицу, введем с клавиатуры имя вектора и знак присваивания. Затем щелкнем по кнопке и откроем окно диалога определения размеров матрицы: П  осле этого заполним массив пустых полей, получим на экране монитора 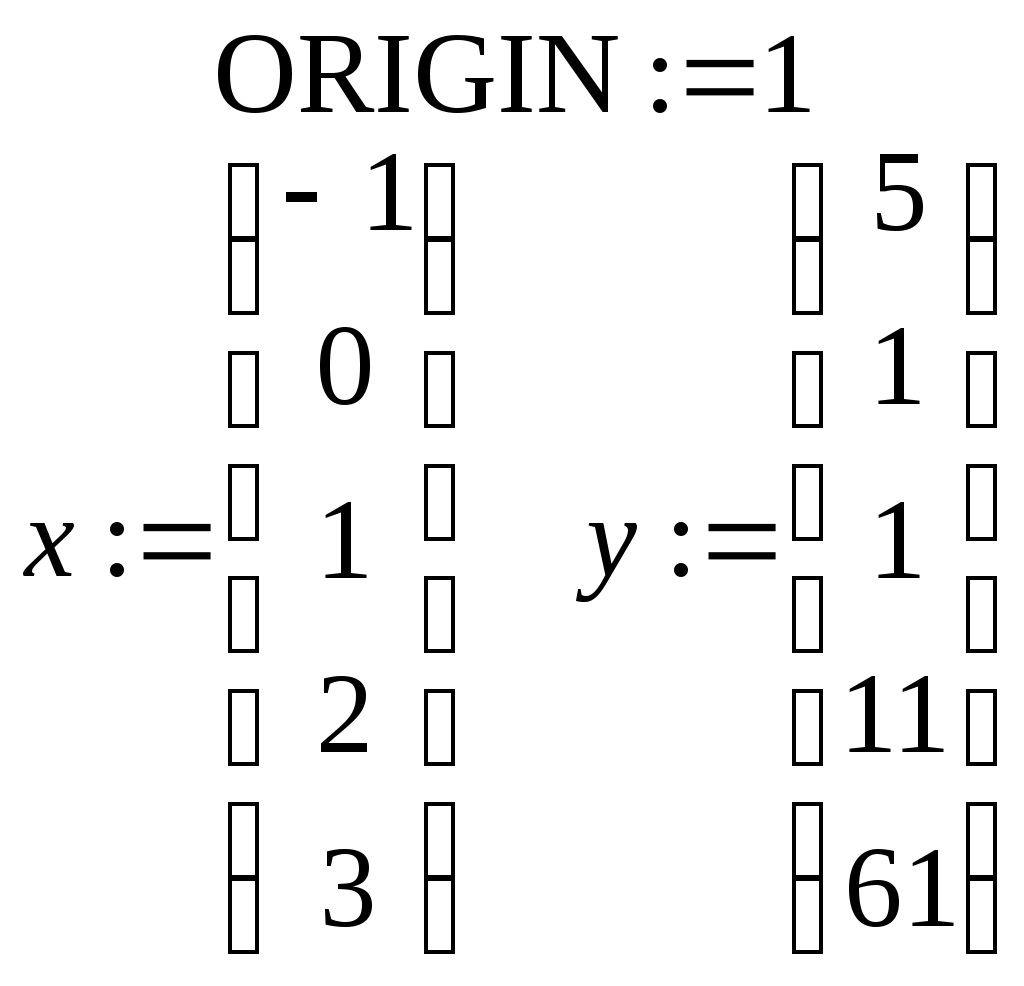 Переменная ORIGIN определяет начало нумерации строк и столбцов матрицы в пакете Mathcad, она описана в предыдущей лабораторной работе. Для определения таблицы (2.9.1) нужно задать функциональную, а не числовую матрицу, поэтому набираем 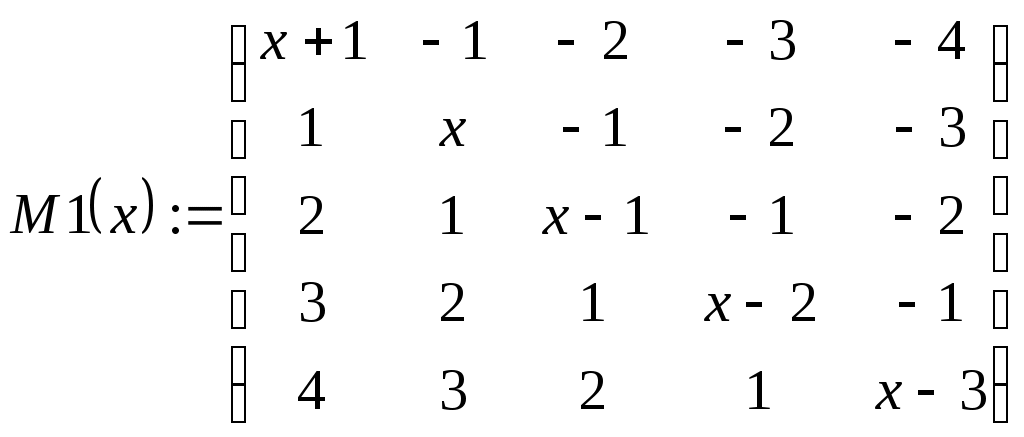 Д  алее вычисляем лагранжевы коэффициенты по формуле (2.9.2). Для этого необходимо преобразовать символьное выражение. Кнопка - Calculus Palette (Панель операций математического анализа) открывает панель, с помощью которой можно суммировать, дифференцировать, интегрировать, вычислять произведения и находить пределы как числовых, так и символьных выражений. Введем выражение  .Щелчком по строке Simplify (Упростить) меню Symbolics (Символьные вычисления) символьному процессору передается выражение, выделенное в рабочем документе, а преобразованное выражение отображается в рабочем документе ниже или справа от исходного выражения в зависимости от задания стиля выражения (Evaluation Style). В 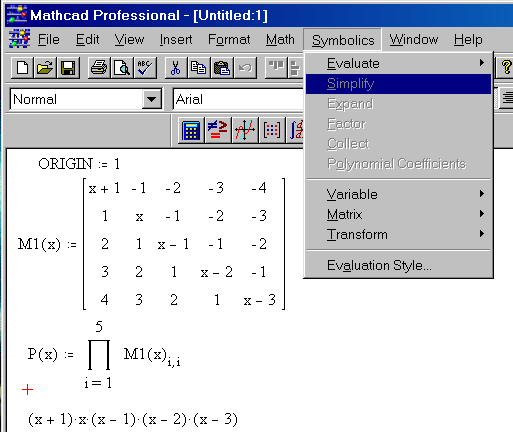 нашем случае получим на экране 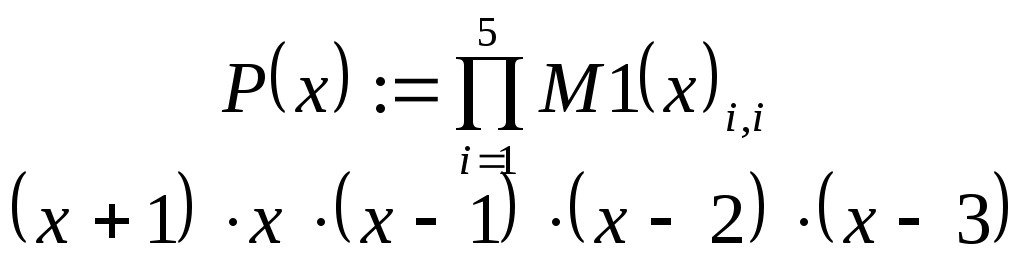 Аналогично вычисляются знаменатели формулы (2.9.2): 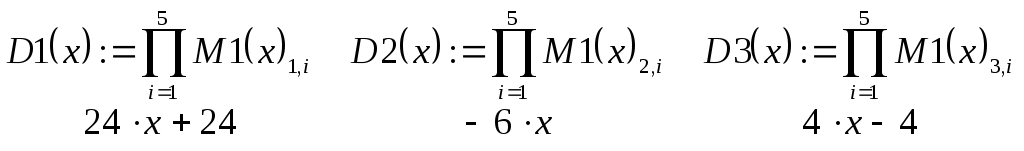 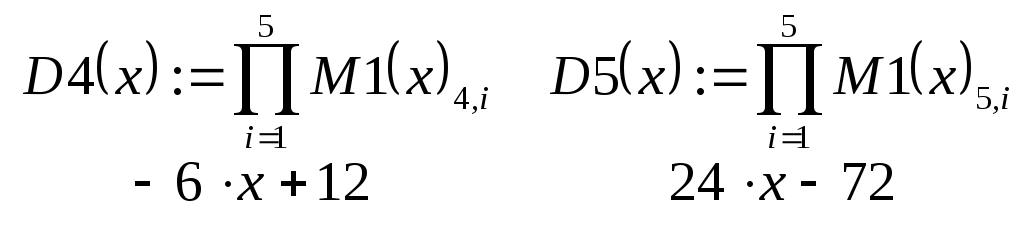 Далее таким же образом вычисляем лагранжевы коэффициенты: 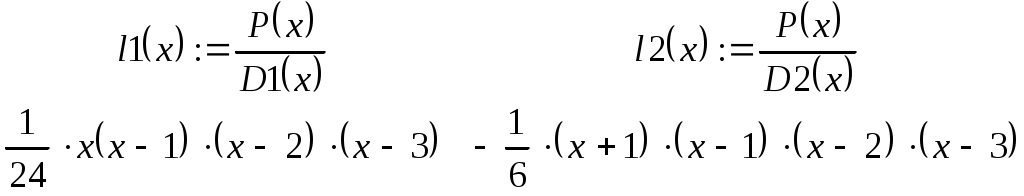 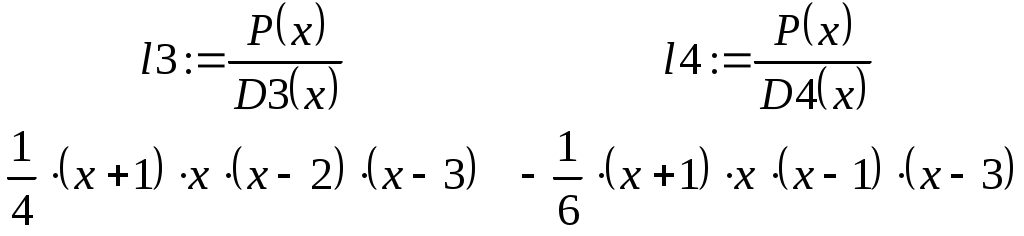 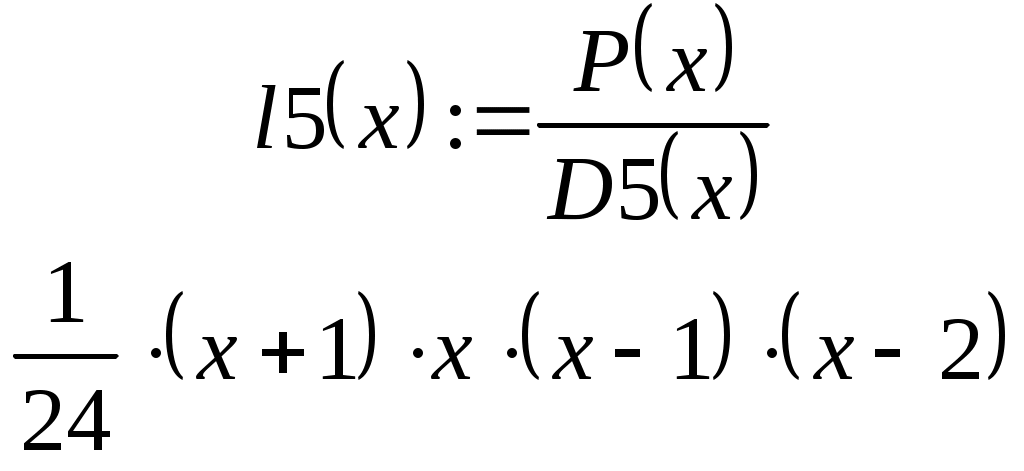 Наконец, получим сам многочлен Лагранжа:  По найденной формуле можно приближенно рассчитывать значения функции в любых точках как внутри, так и вне табличного интервала  с точностью, определяемой теоремой 2.2 (подразд. 2.4), например,  Решим теперь задачу задания № 2. Пусть задана таблицей и 
П  остроим сначала, как описано в предыдущей лабораторной работе, график этой зависимости: Далее последовательно строим числовую матрицу (2.9.3) схемы Эйткена при помощи дискретного аргумента:  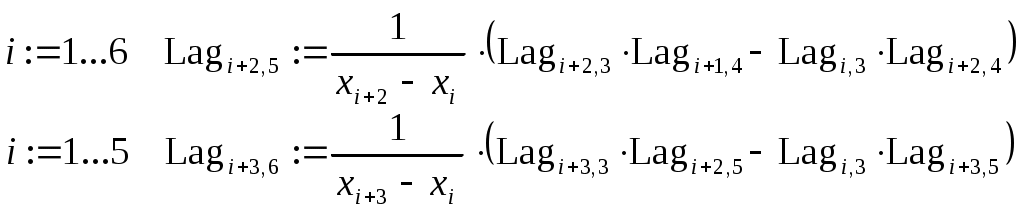 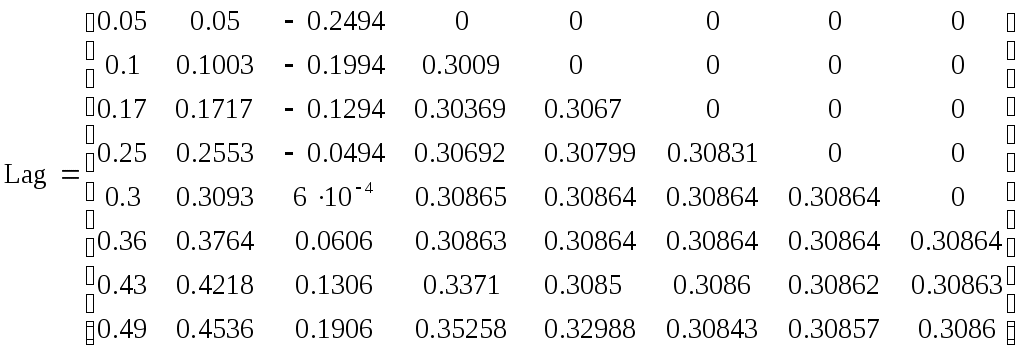     Во всех приведенных таблицах задано пять знаков после запятой в данных, выводимых на дисплей. Это сделано таким образом. После двойного щелчка левой мыши открывается окно ввода параметров настройки отображения чисел, затем выставляется цифра 5 в верхнем окошке. К сожалению, записать двойной цикл и вычислить все в одну строку с помощью дискретного аргумента здесь не удастся, так как, во-первых, нельзя в пакете Mathcad определять простую переменную через дискретный аргумент, во-вторых, переменные, определяющие дискретный диапазон, также не могут определяться через предыдущий дискретный аргумент. Однако эту задачу можно легко решить, составив коротенькую программу вычисления таблицы схемы Эйткена. В  оспользуемся кнопкой -Programming Palette (Панель программи-рования). Она открывает следующую панель: Кнопки этой панели вызывают операторы, во многом аналогичные основным операторам распространенных языков программирования. Язык Mathcad очень напоминает черты языка С. В этом нет ничего удивительного, так как сам Mathcad написан на этом языке. Основными составными операторами являются операторы выбора (if), повторения (until) и цикла (for) с заранее известным числом повторений. Кроме того, введено понятие локальной переменной, операторы досрочного выхода из цикла (break) и (continue) и оператор досрочного выхода из программы (return). К нопка - это команда добавления строки в программу или в тело цикла. С помощью этой кнопки алгоритмические конструкции в программе или цикле могут быть сделаны сколь угодно большими. При нажатии этой кнопки в окне рабочего документа появляется конструкция вида . Вертикальная линия объединяет отдельные операторы в операторный блок с одним входом и одним выходом, выполняющийся как единый оператор. Кнопка -это оператор присваивания значения локальной переменной. К нопка вводит в программы альтернативу с одним плечом (  неполная альтернатива). В первый квадратик (левее if ) записывается выполняемый оператор, в правый - булево выражение. Выполняемый оператор исполнится, если булево выражение возвращает значение «Да» (в среде Mathcad – любое числовое значение, отличное от нуля). Для организации полной альтернативы используется кнопка с оператором otherwise . Кнопка -это кнопка цикла с проверкой. В правый квадратик записывается булево выражение, управляющее цик- л ом, в нижний – тело цикла. Кнопка вводит в программы цикл с параметром. В первый квадрат вводится переменная цикла, в правом (после знака ) указываются пределы изменения этого параметра. Эти пределы можно просто перечислять через запятую или указывать в том виде, как для дискретной переменной:  В нижний квадрат помещается тело цикла.К нопки и позволяют досрочно выходить из циклов while и for , а кнопка - из всей программы. При этом оператор break передает управление обязательно в конец цикла, а оператор continue - в любое место цикла. Н аконец, кнопка вводит оператор обработки ошибок. Если при выпол- н ении оператора в правом квадрате возникнет ошибка, то будет выполняться оператор из левого квадрата. Оператор on error полезен в тех случаях, когда ошибку сложно локализовать, тем более что в программах пакета Mathcad, к сожалению, невозможно выводить на дисплей промежуточные результаты расчета. Итак, программа расчета матрицы схемы Эйткена может быть, например, такой: П 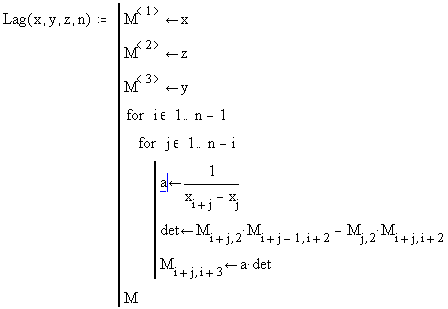 араметрами программы являются вектора исходных данных 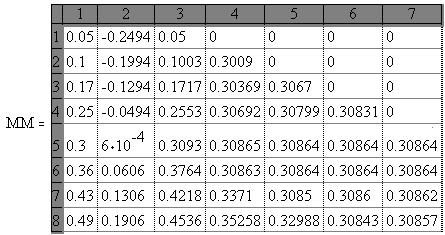 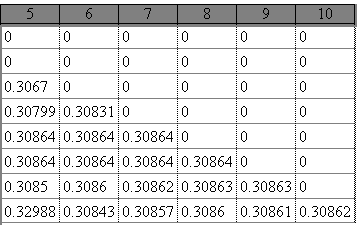. Компоненты вектора  равны:  ,  - число точек табличного задания функции . Для получения матрицы по схеме Эйткена необходимо определить лишь вектор и саму матрицу  :    |
