2. Приближение функций Задача приближения функций

• Название: 2. Приближение функций Задача приближения функций
• Дата: 16.04.2022
• Размер: 7.11 Mb.
• Имя файла: 2-2.12-1.doc
• Тип: Задача; #478932
• страница: 2 из 14

2.3. Полиномиальная интерполяция. Многочлен Лагранжа

Если в качестве базисной взять систему степенных функций, то есть , то получаем задачу полиномиальной интерполяции:

(2.3.1)

Теорема 2.1. Существует единственный интерполяционный многочлен степени , удовлетворяющий условиям (2.3.1).

В качестве искомого многочлена возьмем многочлен степени вида

(2.3.2)

Таким образом, система функций, по которой строится интерполяционный многочлен, есть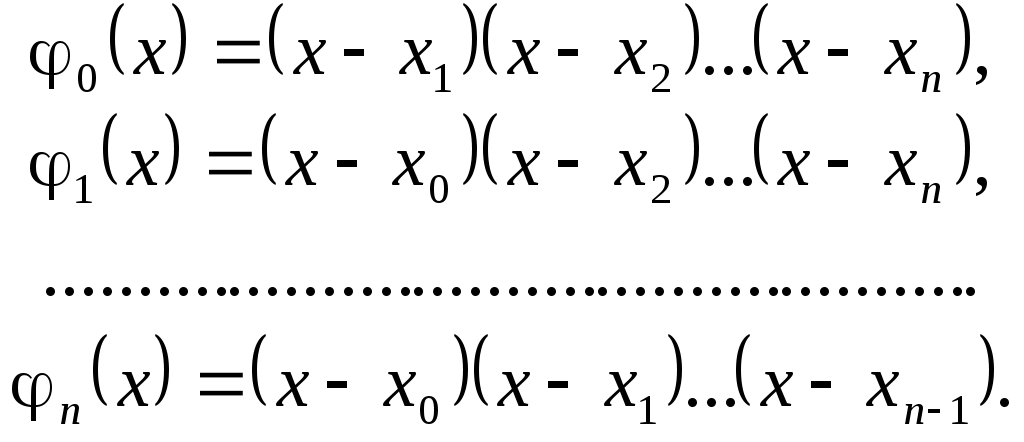



Для нахождения надо

найти набор коэффициентов

. Не будем сос-

тавлять и решать систему

линейных уравнений вида

(2.2.1), найдем коэффициен-

... ты иным способом.

Пусть , с учетом получим



Аналогично, полагая 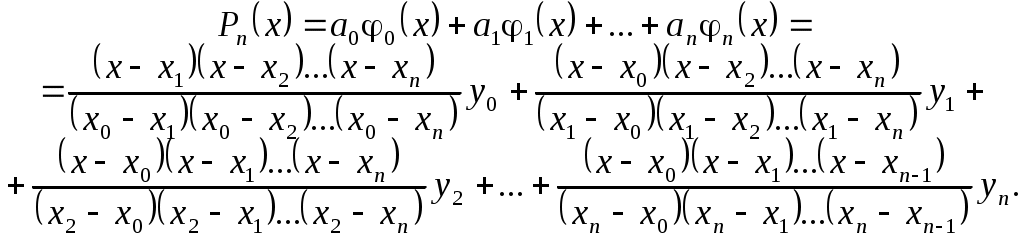и учитывая, что будем иметь



Если , то Тогда сам многочлен будет иметь вид

(2.3.3)

Эта формула называется интерполяционной формулой Лагранжа. Приведем ее в сокращенной записи:

(2.3.4)

Очевидно, представляет собой многочлен степени , удовлетворяющий условию



Таким образом, степень многочлена равна , при в формуле (2.3.4) обращаются в нуль все слагаемые, кроме слагаемого с номером , равного .

Выпишем отдельно многочлены Лагранжа первой и второй степени, ибо именно они чаще всего используются на практике.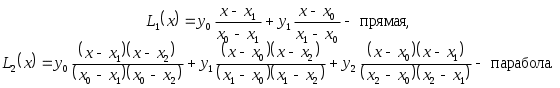

(2.3.5)

Пример. Написать интерполяционный многочлен Лагранжа для функции , значения которой заданы таблицей

	0	1	2	3
	0	0.1	0.3	0.5
	-0.5	0	0.2	1.0

В данном случае 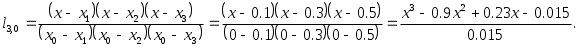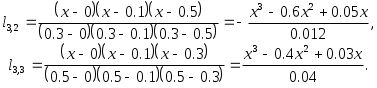, получаем при интерполяции кубическую параболу. Вычислим вначале :



, но его значение не понадобится, так как . Не будем его вычислять.



Тогда искомый интерполяционный многочлен Лагранжа третьей степени будет выглядеть так