2. Приближение функций Задача приближения функций
 Скачать 7.11 Mb.
|
2.7. Интерполяционный многочлен НьютонаПусть функция  задана в  точках таблично, то есть известны
Алгебраический многочлен 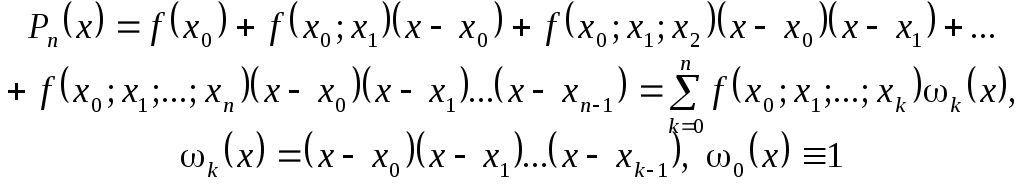 -й степени (2.7.1)называется интерполяционным многочленом Ньютона с разделенными разностями. Очевидна аналогия формулы (2.7.1) с формулой Тейлора. Действительно, так как по теореме 2.7  то   Формулы подраздела 2.4 о погрешности интерполяции  в точке  , не являющейся узловой, можно уточнить следующим образом:  (2.7.2)В практическом плане формула (2.7.1) обладает рядом преимуществ перед формулой Лагранжа. Если, например, по каким-либо причинам необходимо увеличить степень интерполяционного многочлена на единицу, добавив в таблицу еще один узел  , то при использовании формулы Лагранжа это приведет не только к увеличению числа слагаемых, но и к необходимости вычислять каждое из них заново. В то же время для вычисления  по формуле Ньютона (2.7.1) достаточно добавить к лишь очередное слагаемое, так как  Если величина  мала, а функция достаточно гладкая, то справедлива оценка:  из которой, с учетом предыдущего равенства, следует, что Тогда величину  (2.7.3)можно использовать для практической оценки погрешности интерполяции. |
