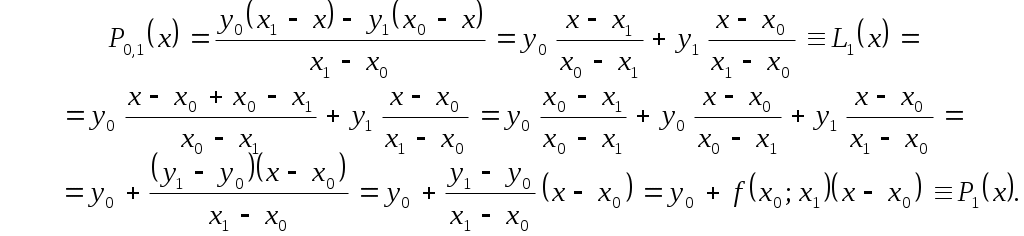Согласно этой схеме интерполяционные многочлены любого вида вычисляются последовательно по формулам
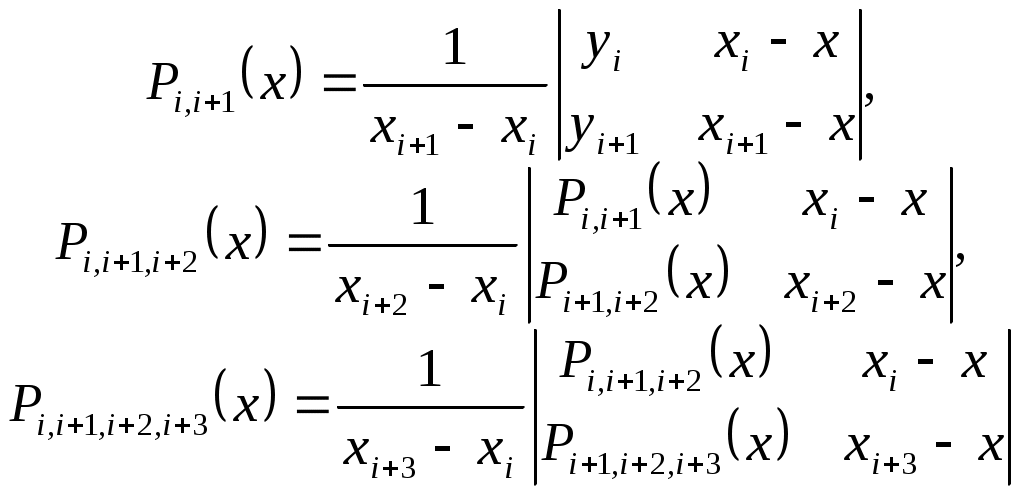 (2.8.1) (2.8.1)
и так далее. Интерполяционный многочлен 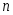 -й степени, принимающий в точках -й степени, принимающий в точках 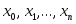 значения значения 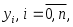 запишется следующим образом: запишется следующим образом:
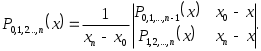 (2.8.2) (2.8.2)
Действительно, из первой формулы (2.8.1) при 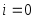 сразу получаем сразу получаем
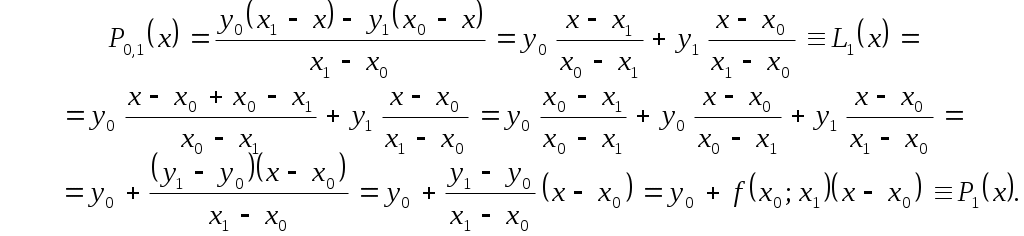
Остальные формулы проверяются аналогично. Кроме того, мы получили, что 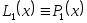 . Это действительно так по теореме о единственности интерполяционного многочлена . Это действительно так по теореме о единственности интерполяционного многочлена 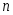 -й степени. Таким образом, -й степени. Таким образом, 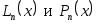 тождественно совпадают и являются по сути лишь разной формой записи единого интерполяционного многочлена тождественно совпадают и являются по сути лишь разной формой записи единого интерполяционного многочлена 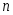 -й степени. -й степени.
Схема Эйткена применяется там, где не нужно общее выражение 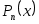 , а нужно лишь его значение при конкретных , а нужно лишь его значение при конкретных 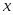 , и при этом значения функции даны в достаточно большом числе узлов. Вычисления по схеме Эйткена удобно вести с помощью таблицы, аналогичной таблице конечных или разделенных разностей: , и при этом значения функции даны в достаточно большом числе узлов. Вычисления по схеме Эйткена удобно вести с помощью таблицы, аналогичной таблице конечных или разделенных разностей:
-
Вычисления прекращают, если 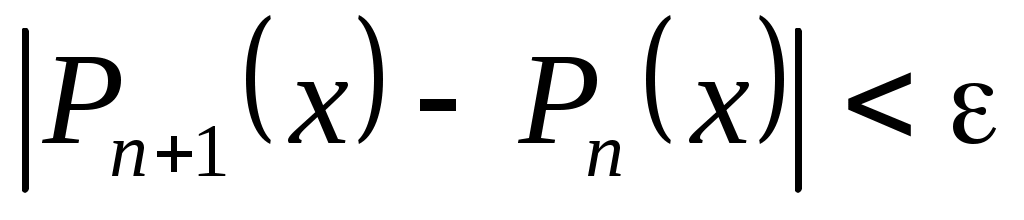 или если последовательные значения или если последовательные значения 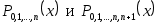 совпадут в пределах заданной точности. совпадут в пределах заданной точности.
Пример. Вычислить 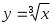 по схеме Эйткена в точке по схеме Эйткена в точке 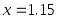 , если , если 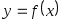 задана таблицей: задана таблицей:
-
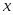
|
1.0
|
1.1
|
1.3
|
1.5
|
1.6
| |
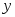
|
1.000
|
1.032
|
1.091
|
1.145
|
1.170
|
Составим таблицу и заполним по формулам (2.8.1) ее столбцы, начиная с четвертого:
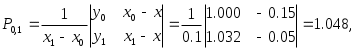
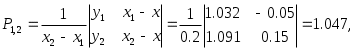
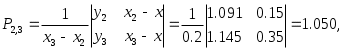
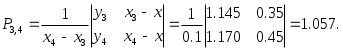
Следующий столбец таблицы заполняется аналогично:
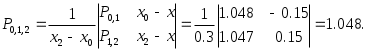
На этом вычисления можно прекратить, так как 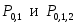 совпадают до третьего знака, следовательно, совпадают до третьего знака, следовательно, 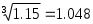 с точностью с точностью 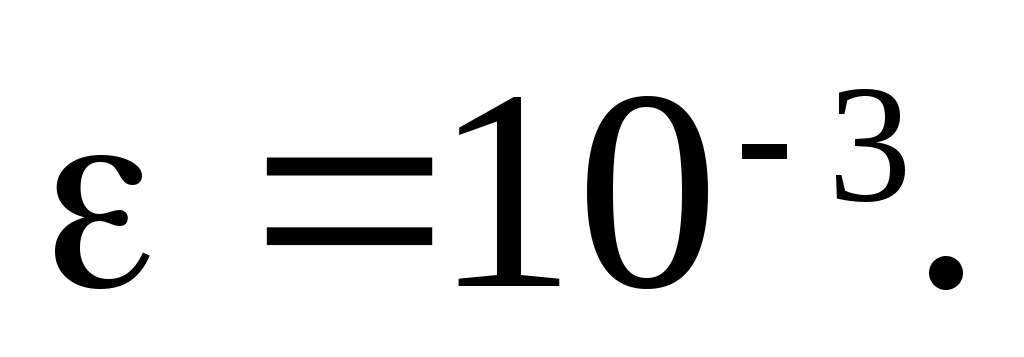 Итоговая таблица с результатами вычислений приведена ниже. Итоговая таблица с результатами вычислений приведена ниже.
-
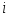
|
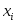
|
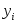
|
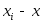
|
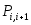
|
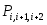
| |
0
|
1.0
|
1.000
|
-0.15
|
|
| |
|
|
|
|
1.048
|
| |
1
|
1.1
|
1.032
|
-0.05
|
|
1.048
| |
|
|
|
|
1.047
|
| |
2
|
1.3
|
1.091
|
0.15
|
|
| |
|
|
|
|
1.050
|
| |
3
|
1.5
|
1.145
|
0.35
|
|
| |
|
|
|
|
1.057
|
| |
4
|
1.6
|
1.170
|
0.45
|
|
| |
 Скачать 7.11 Mb.
Скачать 7.11 Mb.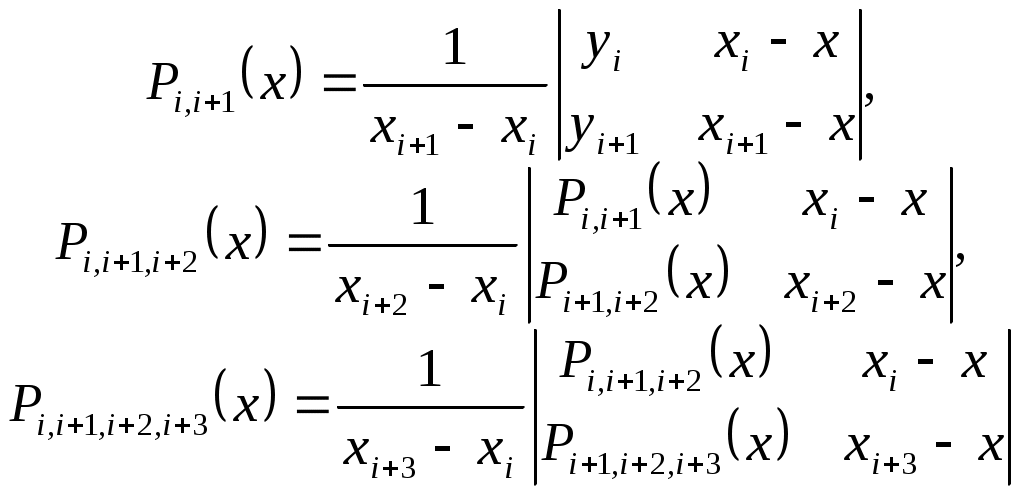 (2.8.1)
(2.8.1)