|
2. Приближение функций 2.1. Задача приближения функций
Вычисление значений функции 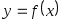 - задача, с которой постоянно приходиться сталкиваться на практике. Часто бывает, что вычисление - задача, с которой постоянно приходиться сталкиваться на практике. Часто бывает, что вычисление 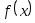 затруднительно, например: затруднительно, например:
1) функция 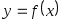 задана таблично задана таблично 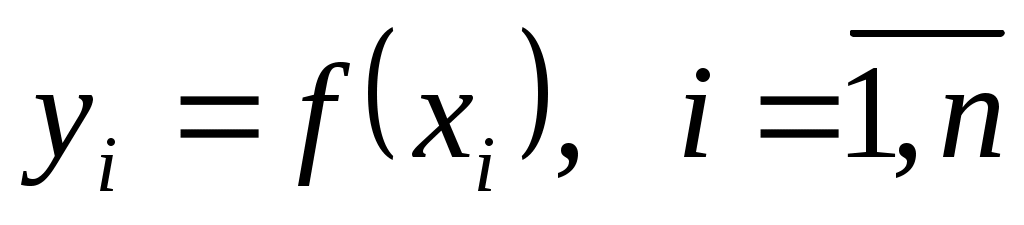 , а вычисление необходимо проводить в точках , а вычисление необходимо проводить в точках 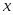 , не совпадающих с табличными; , не совпадающих с табличными;
2) вычисление функции 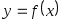 дорого; дорого;
3) для вычисления 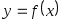 необходим эксперимент. необходим эксперимент.
В таких условиях целесообразно заменить 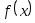 некоторой близкой к ней функцией некоторой близкой к ней функцией 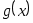 , которая вычисляется быстро и надежно, а погрешность приближения , которая вычисляется быстро и надежно, а погрешность приближения 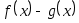 достаточно мала. При этом полезно при выборе функции достаточно мала. При этом полезно при выборе функции 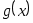 использовать любую дополнительную информацию о функции использовать любую дополнительную информацию о функции 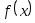 , о ее гладкости, четности, периодичности, монотонности и так далее. Это дает возможность осознанно выбрать класс , о ее гладкости, четности, периодичности, монотонности и так далее. Это дает возможность осознанно выбрать класс 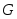 аппроксимирующих функций. аппроксимирующих функций.
Широко используются функции вида 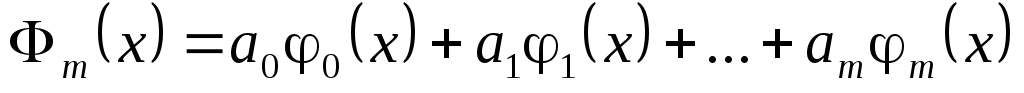 , представляющие собой линейные комбинации некоторых базисных функций , представляющие собой линейные комбинации некоторых базисных функций 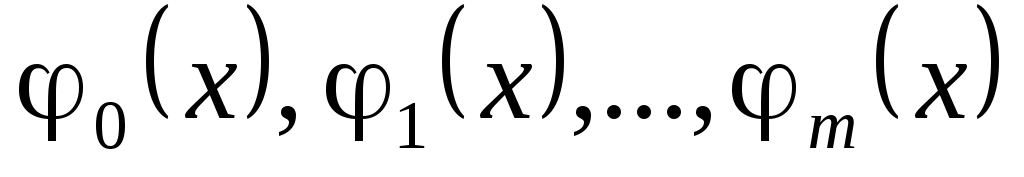 . Функция . Функция 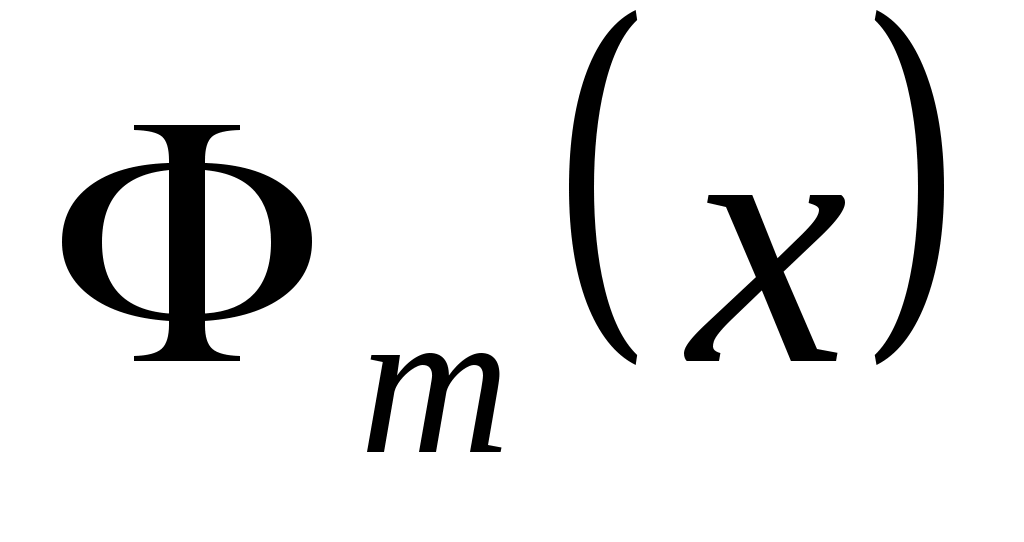 называется обобщенным многочленом степени называется обобщенным многочленом степени 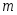 . .
Если ставится требование совпадения функции 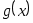 с функцией с функцией 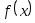 в некоторых фиксированных точках, то это приводит к задаче интерполяции. в некоторых фиксированных точках, то это приводит к задаче интерполяции.
 Построить функцию Построить функцию 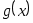 , удов- , удов-
  - - 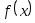 летворяющую условиям летворяющую условиям 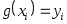 , ,
  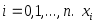 - узлы интерполяции. - узлы интерполяции.
   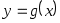 Очевидно, что выбор Очевидно, что выбор 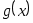 неодноз- неодноз-
 чен, так как по заданной табли- чен, так как по заданной табли-
це можно построить бесконечно
 много интерполирующих функций. много интерполирующих функций.
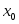 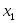 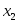 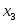 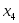 ... ... 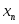
Рассмотрим обобщенный многочлен 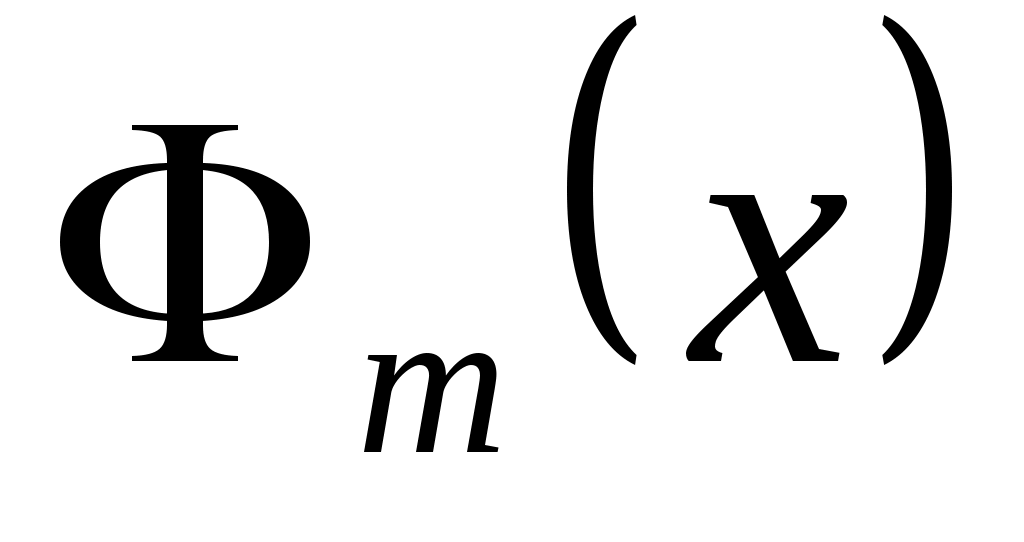 , удовлетворяющий условию , удовлетворяющий условию 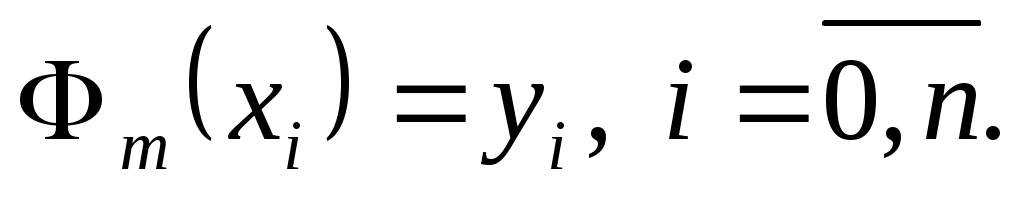 Эта формула, представленная в виде Эта формула, представленная в виде 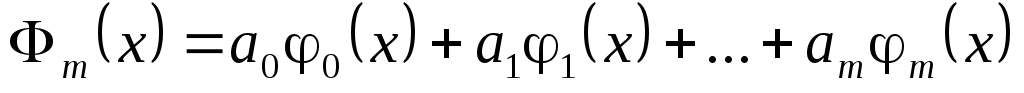 , очевидно, эквивалентна следующей системе линейных алгебраических уравнений: , очевидно, эквивалентна следующей системе линейных алгебраических уравнений:
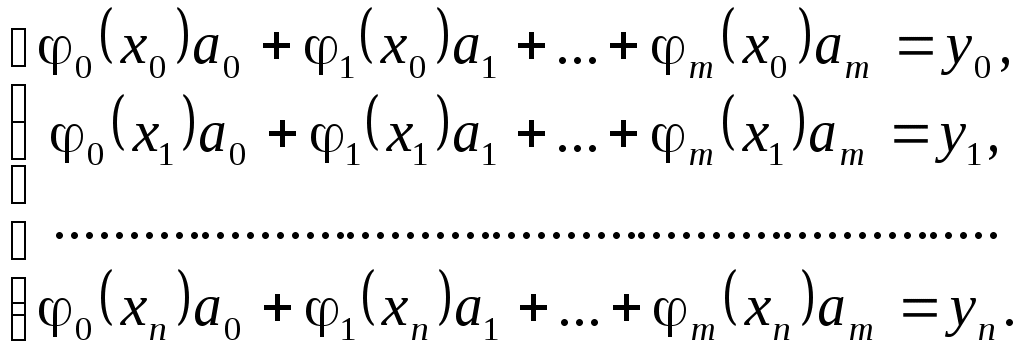 (2.2.1) (2.2.1)
Для определения 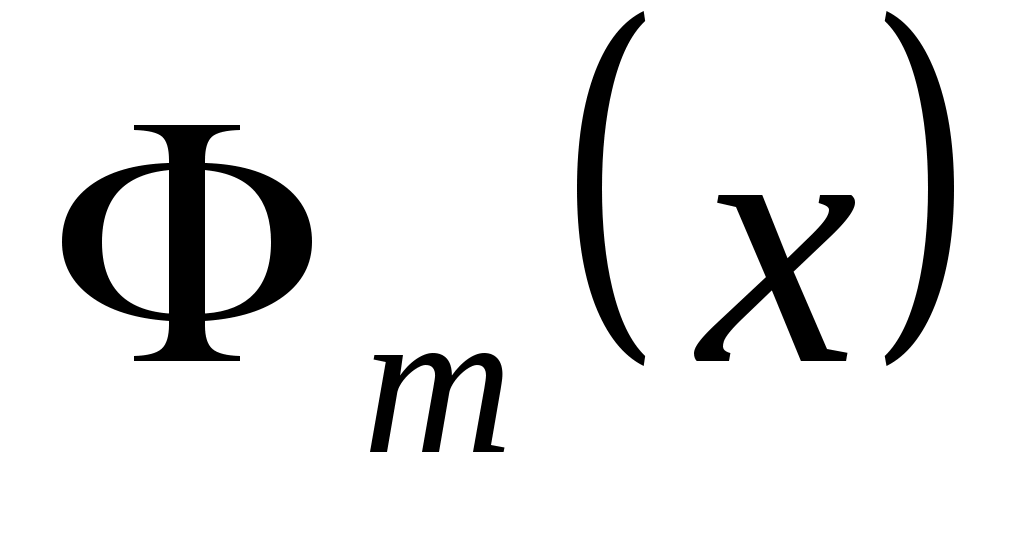 необходимо решить систем (2.2.1) относительно необходимо решить систем (2.2.1) относительно 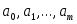 . На практике это делается чрезвычайно редко. Как правило, система (2.2.1) плохо обусловлена. В большинстве приложений используются специальные явные формулы для записи . На практике это делается чрезвычайно редко. Как правило, система (2.2.1) плохо обусловлена. В большинстве приложений используются специальные явные формулы для записи 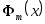 и вычисление и вычисление 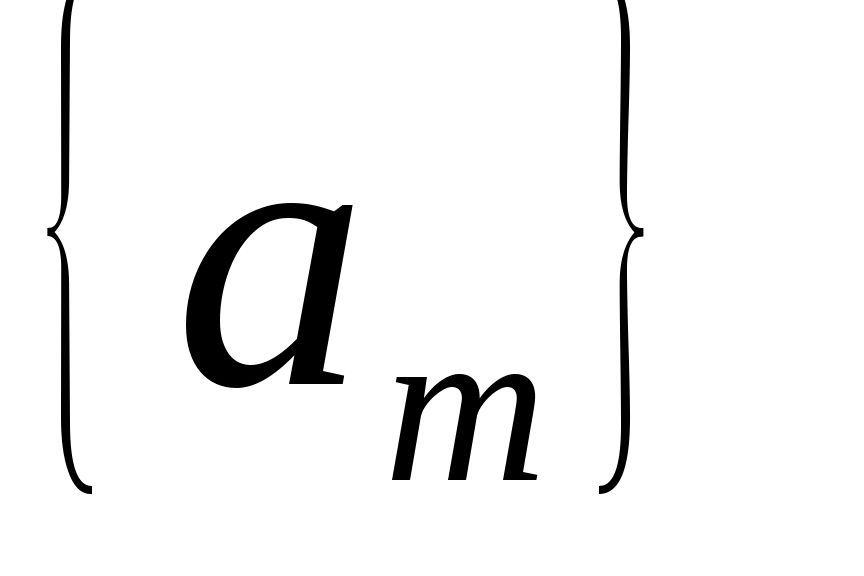 не нужно. не нужно.
|
 Скачать 7.11 Mb.
Скачать 7.11 Mb. Построить функцию
Построить функцию 
 -
- 




 чен, так как по заданной табли-
чен, так как по заданной табли- много интерполирующих функций.
много интерполирующих функций.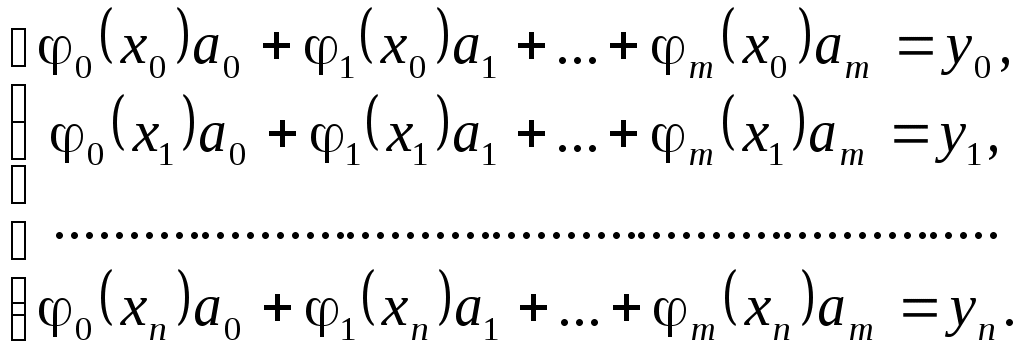 (2.2.1)
(2.2.1)