|
|
2. Приближение функций Задача приближения функций
Теорема 2.2. Пусть функция 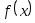 дифференцируема дифференцируема 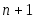 раз на отрезке раз на отрезке 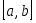 , содержащем узлы интерполяции , содержащем узлы интерполяции 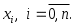 Тогда для погрешности интерполяции в точке Тогда для погрешности интерполяции в точке 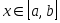 справедливо равенство справедливо равенство 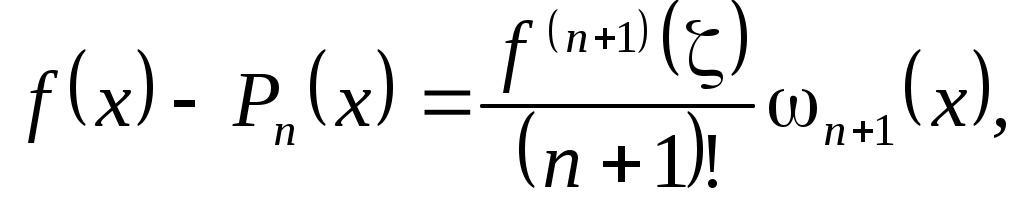 в котором в котором 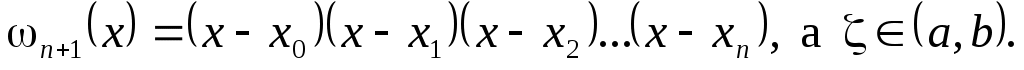
Последнюю формулу несколько модернизируют. Так как положение
точки 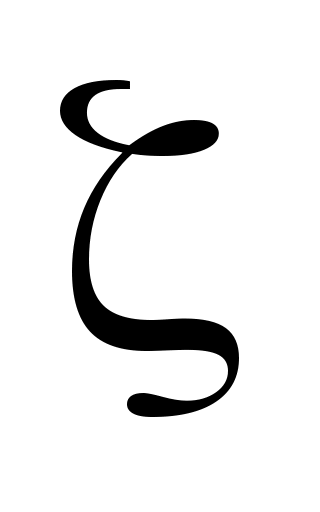 неизвестно, то неизвестно, то 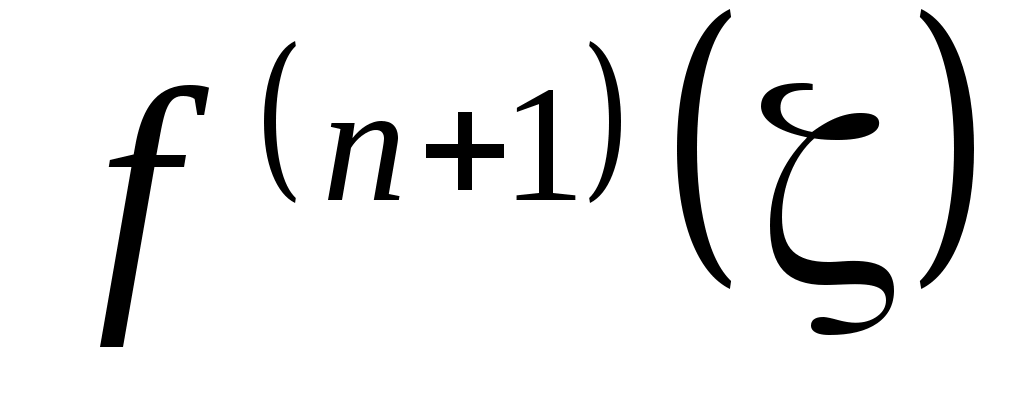 заменяют на заменяют на 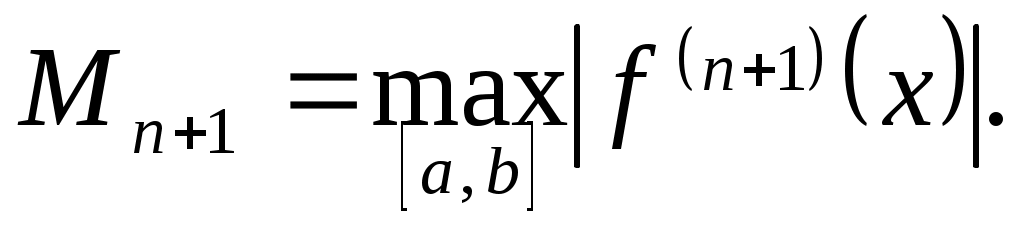 Тогда Тогда
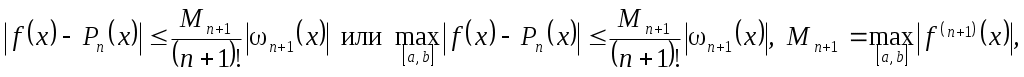 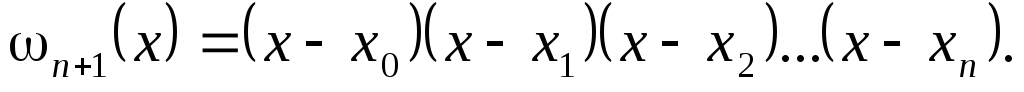
Пример. Вычислим значение 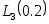 в предыдущем примере и оценим точность полученного значения: в предыдущем примере и оценим точность полученного значения:
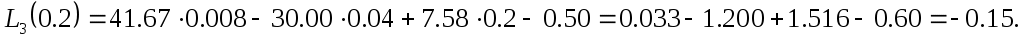
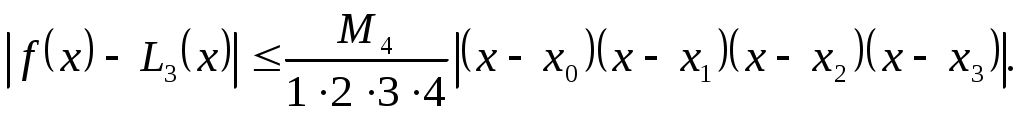
П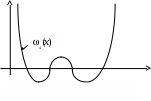 редставление о типичном характере функции редставление о типичном характере функции 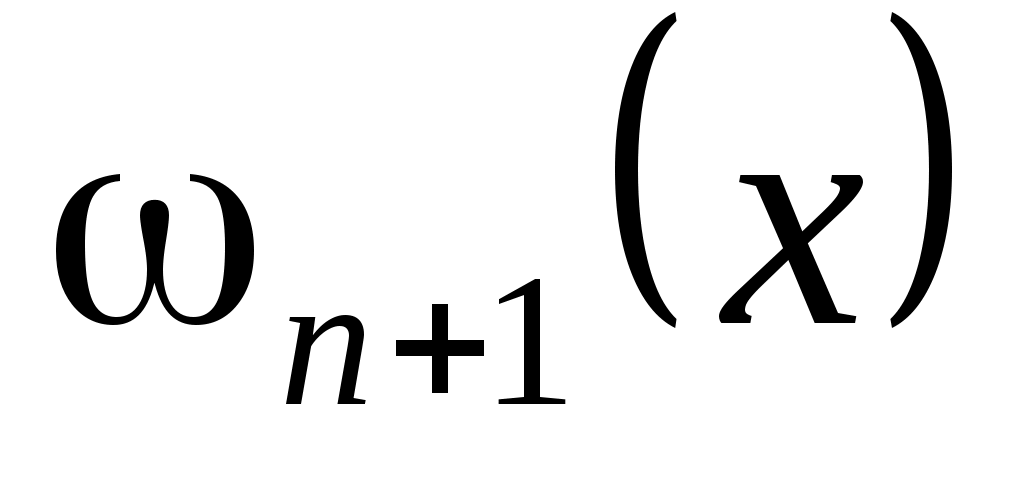 дает график слева. При выходе дает график слева. При выходе 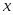 за пределы значений аргумента за пределы значений аргумента 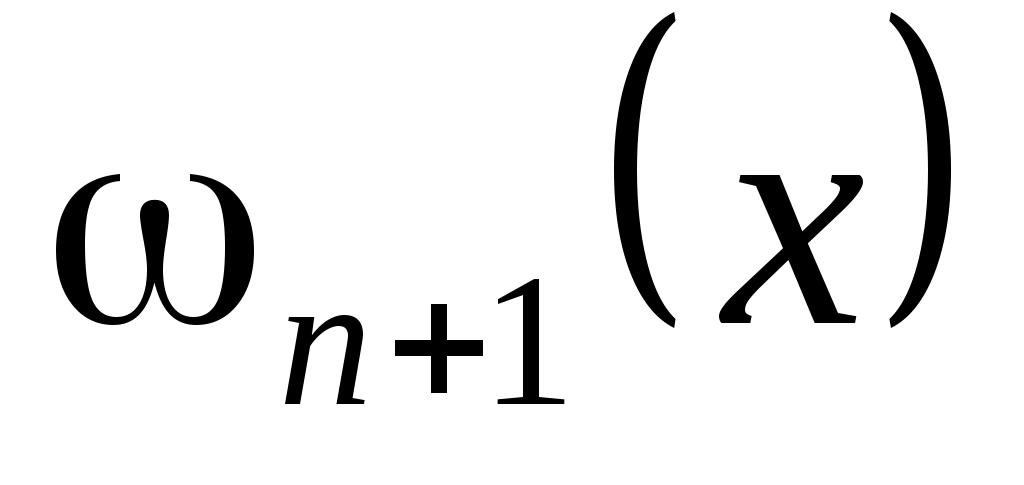 быстро стремится к плюс бесконечности. Несколько огрубляя оценку погрешности, можно получить быстро стремится к плюс бесконечности. Несколько огрубляя оценку погрешности, можно получить 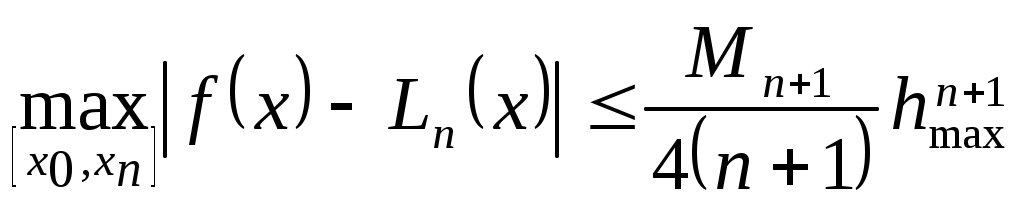 , где , где 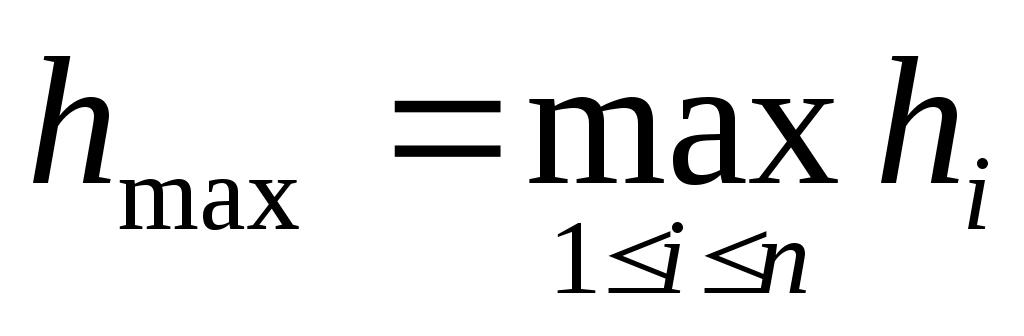 . В нашем случае . В нашем случае 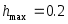 и и 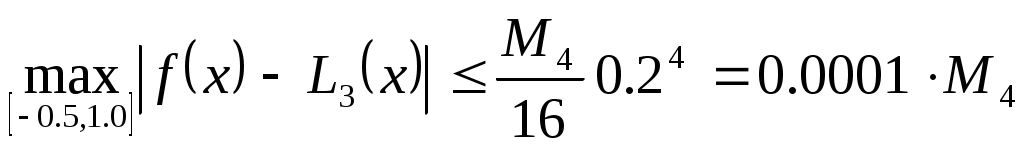 . Сколь-нибудь достоверную оценку . Сколь-нибудь достоверную оценку 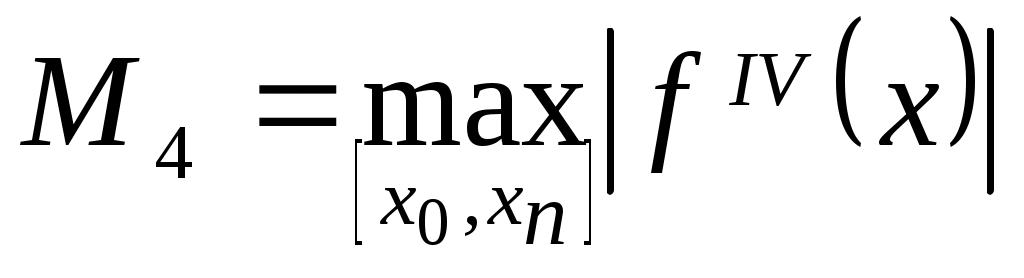 здесь получить невозможно. Если предположить здесь получить невозможно. Если предположить 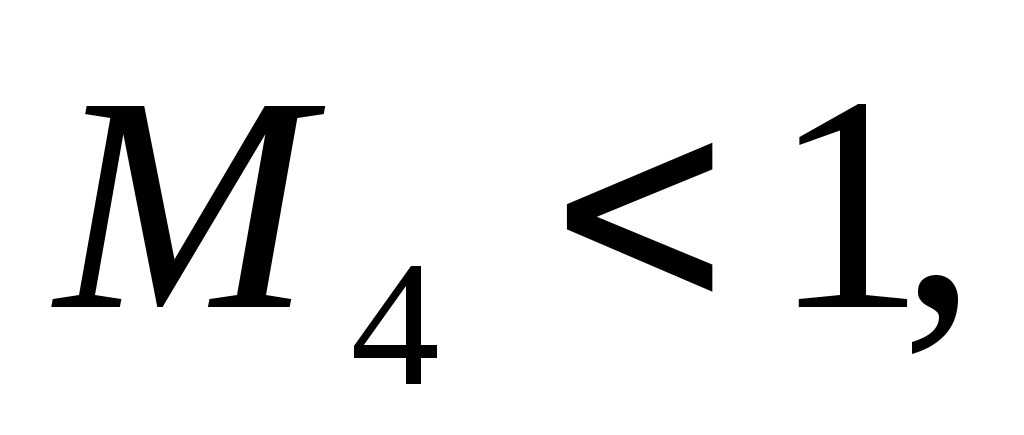 то то 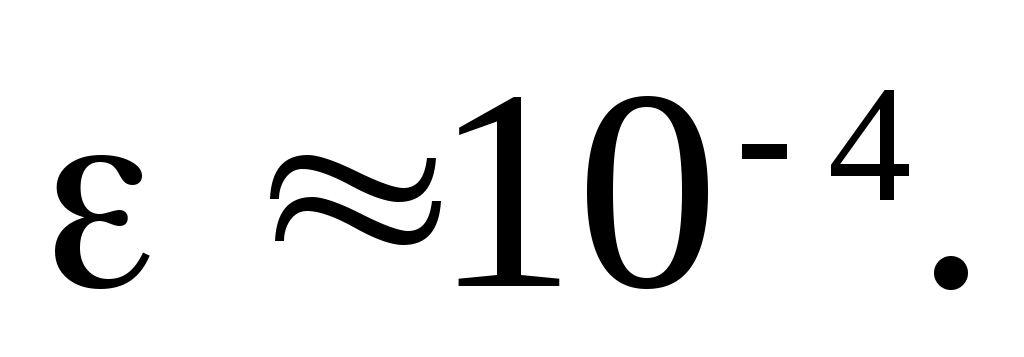
2.5. Конечные разности и их свойства
Пусть функция 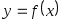 задана таблично задана таблично 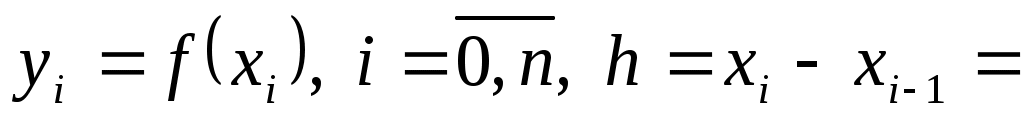 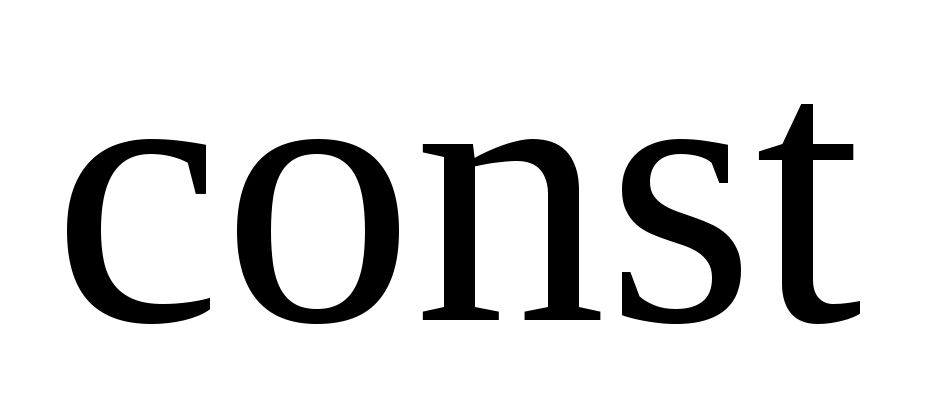 - шаг таблицы, - шаг таблицы, 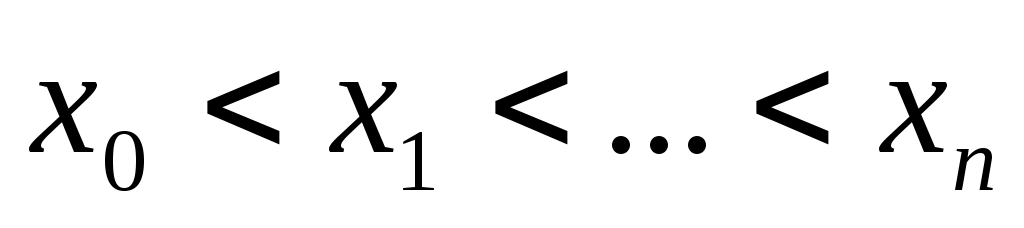 - узлы таблицы. - узлы таблицы.
Величина 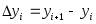 называется конечной разностью первого порядка функции называется конечной разностью первого порядка функции 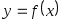 в точке в точке 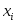 с шагом с шагом 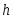 . .
Конечная разность порядка 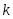 функции функции 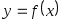 в точке в точке 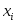 есть есть 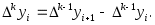 Таким образом, конечная разность второго порядка есть Таким образом, конечная разность второго порядка есть 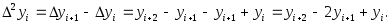 Аналогичным образом могут быть определены конечные разности произвольного порядка. Аналогичным образом могут быть определены конечные разности произвольного порядка.
Конечные разности чаще всего располагают в виде таблицы следующим образом:
-
Теорема 2.3. 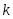 -я конечная разность выражается через значения функции в -я конечная разность выражается через значения функции в 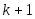 точке по формуле точке по формуле 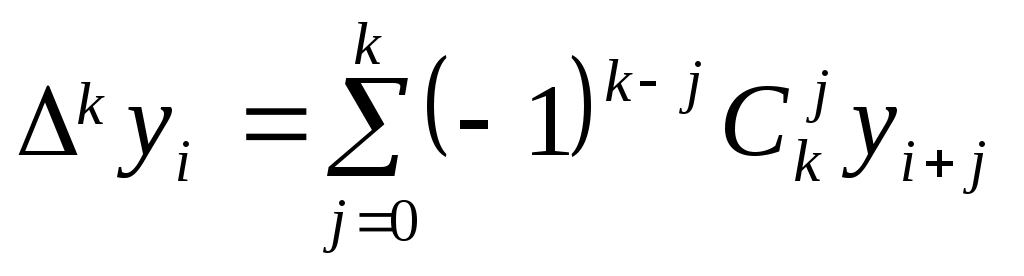 , где , где 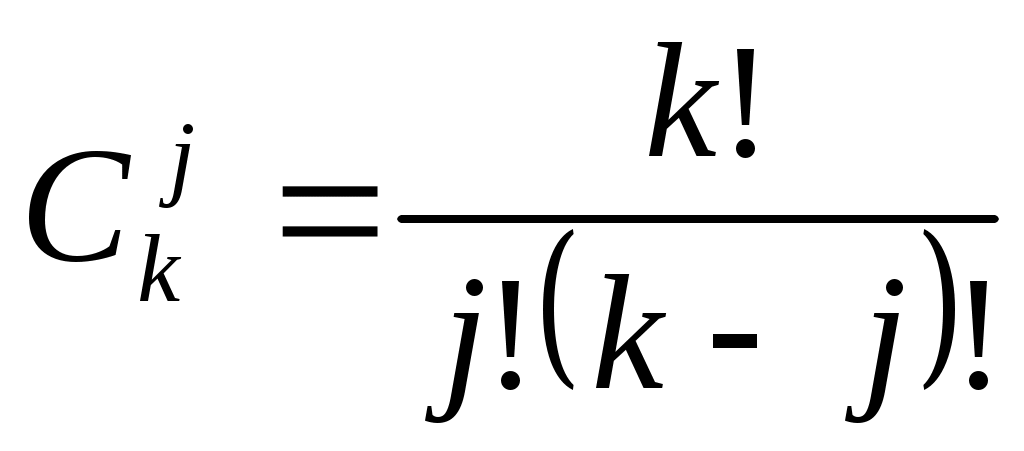 . (2.5.1) . (2.5.1)
В частности уже получена 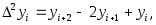 аналогично получаются формулы аналогично получаются формулы
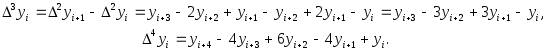
Коэффициенты, входящие в эти формулы, можно взять из треугольника Паскаля.
Теорема 2.4. Пусть функция 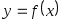 дифференцируема дифференцируема 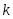 раз на отрезке раз на отрезке 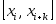 . Тогда справедливо равенство . Тогда справедливо равенство 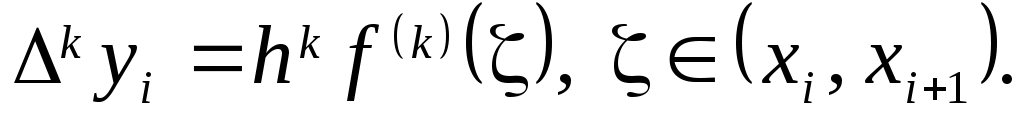 (2.5.2) (2.5.2)
Доказательство
Теорема в общем виде доказывается по индукции. Проверим ее выполнимость только для 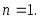
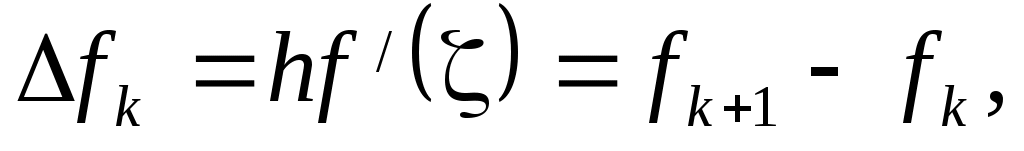 то есть то есть 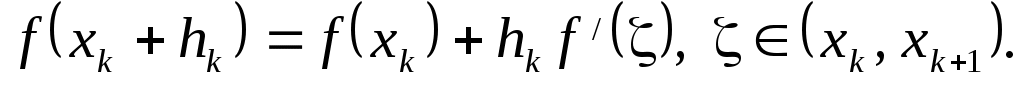
Но последняя формула - формула Лагранжа для 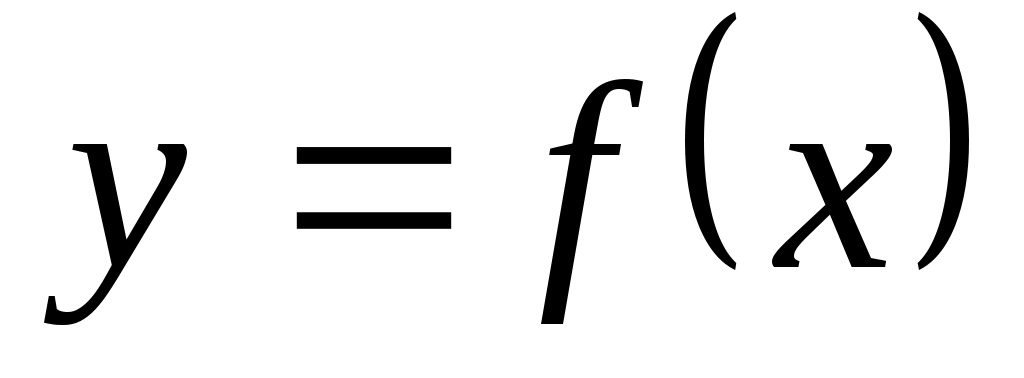 . Для последующих . Для последующих 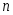 теорема доказывается по индукции. Эта формула может быть применима для оценки погрешности при интерполяции, когда функция задана только таблично. Если теорема доказывается по индукции. Эта формула может быть применима для оценки погрешности при интерполяции, когда функция задана только таблично. Если 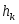 мало, то мало, то 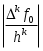 можно приближенно принять за можно приближенно принять за 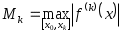 и, таким образом, оценить погрешность и, таким образом, оценить погрешность 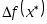 . .
В реальных вычислениях таблица конечных разностей 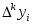 строится по значениям строится по значениям 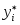 , каждое из которых содержит погрешность , каждое из которых содержит погрешность 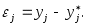 Тогда в силу формулы (2.5.1) вычисленные значения Тогда в силу формулы (2.5.1) вычисленные значения 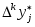 содержат неустранимые ошибки содержат неустранимые ошибки
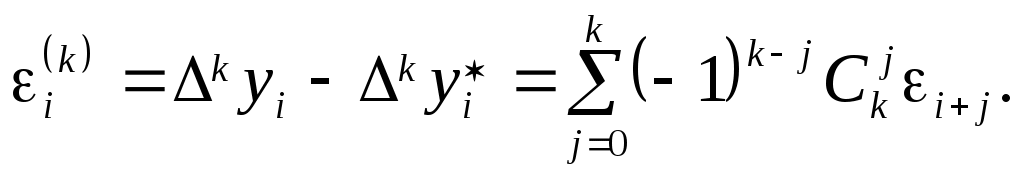 (2.5.3) (2.5.3)
Пусть 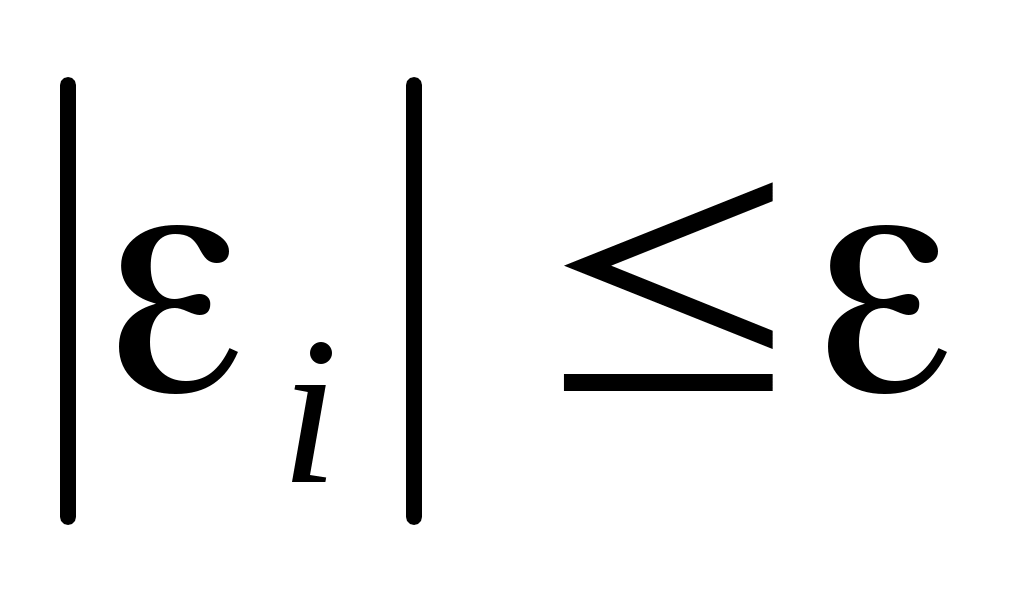 для всех для всех 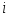 , тогда можно получить гарантированную оценку , тогда можно получить гарантированную оценку
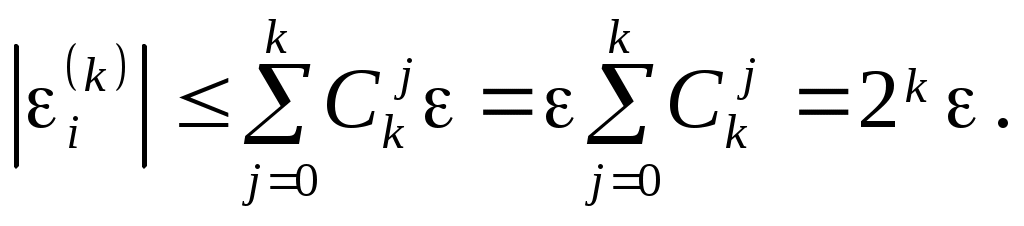 (2.5.4) (2.5.4)
|
|
|
 Скачать 7.11 Mb.
Скачать 7.11 Mb. редставление о типичном характере функции
редставление о типичном характере функции 
