Метод k-моделирования. МЕТОД К-моделирования. 3. каузальное моделирование популяций

• Название: 3. каузальное моделирование популяций
• Анкор: Метод k-моделирования
• Дата: 25.04.2022
• Размер: 2.74 Mb.
• Имя файла: МЕТОД К-моделирования.doc
• Тип: Документы; #496372
• страница: 5 из 12

8. Сети Петри

8.1. Автоматная сеть

Вернёмся к графу переходов вероятностного автомата или марковского процесса. В методе динамики средних мы рассматривали такой граф только для одного элемента системы. Мы приписывали вес равный вероятности или интенсивности перехода каждой дуге графа и этого было достаточно для написания дифференциальных уравнений динамики системы. Запишем в каждую вершину q_i число элементов N_i, находящихся в нём. Вектор, приписывающий число каждой вершине, называется маркировкой M_t = {N_i(t) | i=1..n}, а граф переходов с заданной маркировкой – это автоматная сеть. Такую сеть мы уже использовали для анализа марковских систем и систем массового обслуживания методом динамики средних.

Автоматная сеть позволяет наглядно изобразить полное состояние однородного ансамбля автоматов, но недостаточна для изображения взаимодействий в сложной системе. Следующий шаг в моделировании сложных систем сделан в сетях Петри.

8.2. Каноническая сеть Петри

Сеть Петри позволяет изобразить не только полное состояние сложной системы, но и зависимости переходов (q_i  q_j) от состояний других элементов, точнее от маркировки этих «воздействующих» на переход элементов. С этой целью необходимо ввести в сеть ещё один класс вершин, соответствующих переходам. Переходу ставится в соответствие правило исполнения.

Сеть Петри C – ориентированный двудольный граф C = G(QD, E), т.е. граф с двумя типами вершин Q и D, а множество дуг E  (QD)(DQ). Вершины из множества Q = {q₁,q₂,…,q_n} называются позициями и обозначаются символом O (кружок), вершины из множества D = {d₁, d₂, …, d_m} называются переходами и обозначаются символом ▌(черта). Дуги допустимы только между позициями и переходами: (позиция  переход) или (переход  позиция).

Обозначим:

Е – множество дуг,

*d_j – множество входных позиций для перехода d_j (множество позиций, из которых есть дуги в переход d_j),

d_j* – множество выходных позиций перехода d_j.

В общем случае между позициями и переходами может быть несколько дуг. Сеть Петри C – это мультиграф. Чтобы отобразить множественность дуг, каждой паре (q_i, d_j) и (d_j, q_k) ставится в соответствие натуральное число – вес дуги k_ij или k_jk. Это соответствие задают функции предшествованияIn и следования Out. Функции In и Out отражают связи между событиями и условиями и изображаются матрицами инциденции. Строкам матриц инциденции соответствуют позиции, столбцам – переходы. Элементы матриц In и Out равны весам дуг k_ij и k_jk. Функция In(d_j) – вектор-столбец, отображающий веса k_ij всех дуг, исходящих из позиций q_i  *d_j и идущих в переход d_j. Функция Out(d_j) – вектор-столбец, отображающий веса k_jk всех дуг, исходящих из перехода d_j и идущих в позицию q_k  d_j*. По умолчанию величины k_ij и k_jk, т.е. веса всех дуг равны 1.

Переходы сети Петри соответствуют событиям, происходящим в системе, позиции соответствуют условиям наступления этих событий.

На Рис. 8.1. изображена сеть Петри с пятью позициями, двумя переходами и матрицами инциденции In и Out.

Позиции: Q ={q₁, q₂, q₃, q₄, q₅}

Переходы: D = {d₁, d₂}

Входные множества для переходов: *d₁ = {q₁, q₂}, *d₂ = {q₃}

Выходные множества для переходов: d₁* ={q₃}, d₂*  = {q₄, q₅}

Дуги из Q в D: E₁ = {(q₁, d₁), (q₂, d₁), (q₃, d₂)}

Дуги из D в Q: E₂ = {(d₁, q₃), (d₂, q₄), (d₂, q₅)}

Веса дуг показаны и на графе Рис. 8.1., и в матрицах инциденции In иOut.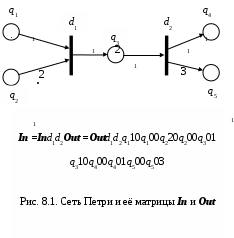

8.3. Маркировка Cетей Петри

Определение Cети Петри позволяет описать статические свойства моделируемой системы, взаимосвязь событий и условий. Для описания динамики вводится функция маркировки M: Q N,где N – множество целых неотрицательных чисел. Маркировка любого подмножества A Q обозначается M(A) и называется частичной. В частности, маркировка входа и выхода в переход d_j обозначаются как M(*d_j) и M(d_j*), соответственно.

Наглядно маркировка изображается точками внутри позиции как показано на Рис. 8.2. Точки называются фишками или маркерами. Таким образом, с помощью функции M позиции сети помечаются целыми неотрицательными числами. Сеть Петри с маркировкой называется размеченной или маркированной. В дальнейшем маркировка сети Петри будет рассматриваться как вектор M =  <M(q₁), M(q₂), …, M(q_n)> = <N₁, N₂, …, N_n>.

8.4. Функционирование сети Петри

Сеть Петри функционирует, переходя от маркировки к маркировке. Последовательность маркирокок называется историей сети Петри C. Начальная маркировка обозначается M₀, а сеть Петри C с начальной маркировкой M₀ задаётся парой <C, M₀>. Смена маркировок происходит в результате срабатывания (запуска) одного из переходов. Переход срабатывает только в том случае, если он разрешен (возбужден).

Переход d_j разрешен, если для всякой входной позиции q_i выполняется условие M(q_i)  k_ij, где k_ij – число дуг из позиции q_iв переход d_j. У разрешенного перехода каждая дуга, входящая в переход, обеспечена фишками в соответствующей входной позиции. Лишние фишки не влияют на запуск. Переход запускается удалением фишек из его входных позиций и образованием новых фишек в его выходных позициях. Запуск перехода меняет маркировку сети Петри. В результате получается новая маркировка M₁, которая определяется следующим образом.

Пусть срабатывает переход d_j, тогда для всякой входной вершины q_i

M₁(q_i) = M(q_i) – k_ij

для всякой выходной вершины q_l

M₁(q_l) = M(q_l) + k_jl

где k_ij– число дуг между q_i и d_j, т.е. k(q_i, d_j);

k_jl – число дуг между d_j и q_l, т.е. k(d_j, q_l).

Если вершина q_i является и входной, и выходной для перехода d_j и k_ij = k_jl, то ее маркировка, очевидно, не меняется. В этом случае говорят, что пара (q_i, d_j) образует петлю.

На Рис. 8.2.(а) изображена сеть Петри с начальной маркировкой M₀ = (1, 1, 0, 0, 0).

В этой маркировке разрешен переход d₁. После его срабатывания получается маркировка M₁ = (0, 0, 1, 0, 0) (Рис. 8.2. (б)) и переход d₂ становится разрешенным. Срабатывание перехода d₂ ведет к маркировке M₂ = (0, 0, 0, 1, 1) (Рис. 8.2. (в)).

Смена маркировки M на M₁ обозначается M d_j > M₁.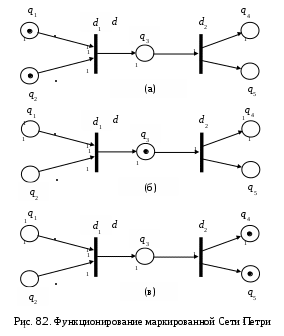


Размеченные сети Петри позволяют описать события произвольной длительности, при этом отображается только порядок следования событий. Выполнение сети начинается при ее начальной маркировке M₀ и проходит через последовательность маркировок, т.е. имеет историю. Историй может быть множество в зависимости от порядка срабатываний переходов. Таким образом, Сеть Петри с начальной маркировкой определяет структуру причинно‑следственных связей в дискретной системе и всевозможные варианты развития параллельных процессов в ней. Для правильного понимания динамики сети Петри важны следующие три предположения о её функционировании.

1. 
   Разрешенный переход не может находиться в этом состоянии бесконечно долго, он обязательно сработает через какое-то конечное время. В обычных сетях Петри это время предполагается случайной величиной. Это предположение вытекает как из физической природы моделируемых систем, так и из соображений «экономии мышления».
   

Зачем вводить переход, который никогда не срабатывает?

2. 
   Переход срабатывает мгновенно, что отражает дискретность поведения моделируемой системы с дискретными событиями.
   
3. 
   В каждый данный момент может сработать только один переход. Иными словами, поток событий и способ исполнения в сети Петри ординарен. Это предположение адекватно только в том случае, когда исполнитель переходов в системе всего один. Например, это процессор для операционной системы. Ординарность потока событий упрощает моделирование процессов в системах и соответствующих сетях Петри. Это предположение позволяет изображать динамику сети Петри в виде графа исполнения G(M,V), где M– множество маркировок, V­– множество дуг, изображающих переходы от маркировки к маркировке. В общем случае ординарность может и не соответствовать природе моделируемой системы.
   

Заметим, наконец, что сеть Петри может функционировать как в дискретном, так и в непрерывном времени. Наиболее сильное и сомнительное условие, принятое в обоих случаях – ординарность потока событий в сети Петри, когда разрешённые переходы срабатывают по одному.

8.5. Представления сети Петри

Ранее были использованы два способа представления сетей Петри: двудольный граф и матрицы инциденции. Правила функционирования сети Петри позволяют ввести подстановочное представление сети Петри, задающее причинно-следственную структуру параллельного процесса в сложной системе и, главное, удобное для ввода в компьютер.

Каждому переходу d_j в сети Петри, ставится в соответствие подстановка следующего вида:

d_j: M(*d_j)  In(d_j)  M(*d_j) – In(d_j), M(d_j*) + Out(d_j), j = 1, 2,…, m

где левая часть задаёт условие срабатывания перехода d_j, а правая – новую частичную маркировку согласно правилам функционирования сети Петри.


Особенно просто выглядит подстановочное представление для ординарных сетей, у которых все k_ij = 1. Тогда маркировки M(*d_j), M(d_j*) изменяются только на 1 и подстановка, имеет вид

d_j: M(*d_j)  1  M(*d_j) – 1, M(d_j*) +1

где единичный вектор 1 вычитается из всех входных маркеров и прибавляется ко всем выходным маркерам перехода d_j. В силу тривиальности условия срабатывания и вычисления новой маркировки, подстановка d_i для ординарной сети Петри допускает более компактный вид:

d_i: In (d_i)  Out(d_i).

Пример 8: На рис. 8.3. показаны различные представления одной и той же сети Петри:

а) Двудольный граф сети Петри

б) Матричное представление сети Петри

в) Система подстановок сети Петри

г) Компактная запись в виде подстановок произведений имен q_i на k_ij, причем k_ij = 1 не пишется, а k_ij  1 изображается либо как коэффициент, либо, как степень.

8.6. Применение аппарата сетей Петри

Сети Петри применяются для моделирования систем, в которых можно выделить дискретное множество событий и условия выполнения и окончания этих событий. Они допускают произвольную интерпретацию элементов модели, что обеспечило их широкое применение. С помощью сетей Петри разрабатывают аппаратное и программное обеспечение ЭВМ, моделируют физические, социальные, биологические системы. Сети Петри используются при разработке систем управления. Существует подход, когда весь процесс проектирования ведется в терминах сетей Петри, а затем производится анализ полученной сети и доказательство корректности проектируемой системы.