Метод k-моделирования. МЕТОД К-моделирования. 3. каузальное моделирование популяций

• Название: 3. каузальное моделирование популяций
• Анкор: Метод k-моделирования
• Дата: 25.04.2022
• Размер: 2.74 Mb.
• Имя файла: МЕТОД К-моделирования.doc
• Тип: Документы; #496372
• страница: 8 из 12

11. Метод компьютерного моделирования популяций

Предметом настоящего раздела является метод моделирования простой популяции автоматов, функционирующей в дискретном времени T= 1, 2, 3, …, t, … с помощью компьютерной программы «Популяция». Вообще говоря, такие системы можно моделировать линейными или нелинейными системами дифференциальных уравнений. Для решения этих уравнений можно использовать известные численные методы, писать программы или использовать готовые системы прикладных программ. Проблема состоит в высокой трудоёмкости этого пути. Между тем построение требуемых уравнений и их численное решение настолько стандартная процедура, что можно ограничиться только заданием К‑сети. Кроме того, в дидактических целях программа должна быть простой, легко управляемой и давать наглядные результаты в виде графиков и массивов результатов моделирования.

11.1. Моделирование простых и автоматных популяций

Пусть N – количество автоматов, n – число состояний, в которых может находиться каждый из автоматов. При этом каждый конкретный автомат не обязательно имеет все n состояний. Популяция может состоять из автоматов различных классов, отличающихся набором состояний и поведением. В каждом i‑том состоянии пребывает N_i автоматов, так что N = N₁ + N₂ + … + N_n(n – натуральное, N_i– неотрицательное действительное при i = 1, …, n). Использование действительных чисел вместо целых позволяет не задавать очень большие числа N_i и избежать погрешности при округлении. В конечном итоге нас все равно интересует только динамика или поведение популяции. При этом можно использовать статистические вероятности и другие статистические характеристики.

В каждом такте, то есть через заданный промежуток времени, количество автоматов в j‑том состоянии изменяется или остается тем же. Это происходит следующим образом. Некоторое состояние i влияет на состояние j и переводит его в состояние k с интенсивностью K(i, j, k). Множество всех таких интенсивностей это трехмерный массив

P= {K(i, j, k) | i = 1..n, j = 1..n, k = 1..n}.

Это означает, что N_i автоматов, находящихся в состоянии i, влияют на N_j автоматов, находящихся в состоянии j, и переводит некоторое их количество M_ijkв состояние k.

При линейном взаимодействии M_ijk= K(i, j, k) min(N_i, N_j),

при взаимодействии в растворе: ;

при нелинейном взаимодействии в смеси: ,

где j = 1, ..., n, то есть одно i‑тое состояние может воздействовать на множество j‑тых. Соотношения и задают вероятность встречи автоматов в i‑том и j‑том состояниях в единичном объёме раствора и смеси.

Обратим внимание, что если никаких других состояний, кроме i и j, в системе нет, то N_i + N_j = N, и интенсивности переходов в растворе и смеси совпадают.

Условие i = j при линейном взаимодействии означает, что автомат, находящийся в состоянии i, самостоятельно переходит в состояние k независимо ни от каких других автоматов. Если все переходы в популяции линейные и для всех переходов i = j, то имеет место линейная автоматная популяция. Такие популяции мы исследовали с помощью автономных вероятностных автоматов.

При нелинейном переходе условие i = j означает, что для взаимодействия необходима встреча двух автоматов в i‑том состоянии, один из которых перейдет в k‑тое состояние с интенсивностью K(i,i,k).

Если при переходах автоматов из одних состояний в другие общее число автоматов N неизменно, то популяция является замкнутой. В замкнутой популяции можно получить статистические вероятности состояний автоматов P_i= N_i /N.

Интерес представляют открытые популяции, где возможно удаление автоматов и появление новых. Для записи этих действий используется внешнее или 0‑состояние q₀, обозначаемое символом «*». Будем считать, что автоматов находящихся в 0‑состоянии всегда достаточно для реализации переходов, а численность 0‑состояний не меняется.

Появление новых автоматов происходит под воздействием уже существующих. Автоматы, находящиеся в состоянии i, добавляют в состояние j новые автоматы с интенсивностью K(i, *, j). Количество появившихся автоматов равно K(i, *, j)N_i при всех типах взаимодействий. Отметим, что при порождении новых автоматов интенсивность – это любое число, соответствующее числу «потомков». Например, пусть рыба мечет 5 тысяч икринок, состояние с – самка, готовая метать икру, и – икринка, 0 – внешнее состояние, тогда K(с,*, и) = 5000.

Удаление автоматов, находящихся в состоянии j, происходит под воздействием уже существующих автоматов, находящихся в некотором i‑том состоянии. Удаление происходит с интенсивностью K (i, j, *), т.е. автоматы в i‑том состоянии «убивают» автоматы в j‑том состоянии с вероятностью p(i, j, *) в окрестности взаимодействия.

В общем случае может оказаться так, что число автоматов, удаляемых из состояния i, будет больше, чем их находится в этом состоянии. В этом случае удаляются только N_i автоматов из числа находящихся в состоянии i, т.е. получается N_i = 0. Эта возможность учтена в формулах для числа удаляемых автоматов. Кроме того, в программе моделирования популяций предусмотрен сторож, не допускающий значения N_i < 0. Обратим внимание, что теорема инвариантности на случай получения N_i < 0 не распространяется.

Итак, изменение количества N_i(t) автоматов в такте t имеет вид:

N_i(t + 1) = N_i (t) + ΔN_i (t), где ΔN_i = V_i – I_i + R_i.

– число автоматов перешедших в i‑тое состояние в такте t;

– число автоматов покинувших i‑тое состояние в такте t;

 – число автоматов, «родившихся» в i‑том состоянии.

Здесь M_ijk вычисляются по формулам приведенным выше.

Чтобы получить среднее количество автоматов в каждом состоянии на (t+1)‑ом шагу, необходимо воспользоваться этими формулами t раз.

Несмотря на ограниченность данного подхода, класс моделируемых популяций включает множество интересных систем, допускающих множество интерпретаций в различных предметных областях. Можно было бы попытаться найти общий метод аналитического решения подобных задач и в переходном, и в стационарном режимах. Мы ограничились описанием аналитических методов поиска стационарных состояний сложных систем, если это возможно. Причина такого ограничения в том, что эта книга и программа «Популяция» написаны не математиками и не для математиков, а инженерами для инженеров и информатиков, а также и для любых специалистов, пытающихся применить точные методы в своей предметной области. Имея программу «Популяция» достаточно описать поведение отдельных элементов исследуемой системы в их связи с другими элементами и получается модель, которая легко модифицируется и быстро даёт наглядные результаты. При этом будет представлено и поведение популяции в переходном режиме. А это уже немало в тех предметных областях, где господствуют качественные рассуждения. Особенно это касается гуманитарных наук.

11.2. Интерфейс программы «Популяция»

Итак, в нашем распоряжении имеется метод математического и компьютерного моделирования сложных систем, который уместно назвать популяционное моделирование. Метод популяционного моделирования был реализован программой «Популяция» для линейных и нелинейных, простых и автоматных популяций, таких, что все переходы в них могут быть заданы фразами вида:

«Состояние i переводит состояние j в состояние k с интенсивностью K(i, j, k). Тип».

Имея это в виду, будем далее записывать переходы К-модели выражением вида

i: j > k;K;0|1|2

где, соответственно:i, j, k – имена состояний: действующего, исходного и результирующего, K – интенсивность перехода, а числа 0, 1 и 2 – альтернативные описания типа перехода: линейный, раствор и смесь.

Интерфейс программы состоит из двух форм: исходная и результирующая. Исходная форма предназначена для задания начального состояния, количества тактов, момента начала моделирования и таблицы переходов (их интенсивности, типа и задержек). Описание исходной формы представлено на Рис. 11.1. Меню «Файл» позволяет сохранять, открывать и редактировать введённые задания.

И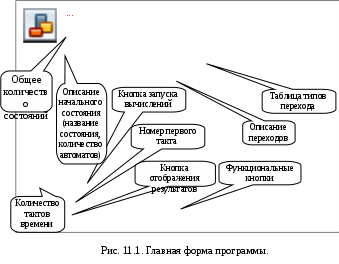
сходные данные о задаче записываются в текстовой файл при нажатии кнопки «Сохранить как» меню «Файл». Формат записи следующий.

1. 
   Первая строка – количество состояний n.
   
2. 
   Следующие 2n строк – имена состояний и их начальное количество.
   
3. 
   Одна строка – k+ 1, где k – количество строк в «Матрице переходов».
   
4. 
   Следующие 7k строк – строки «Матрицы переходов» как они описаны выше. Внешнее состояние задаётся знаком «*». При этом числами в позиции «Тип перехода» следует задать только нелинейные переходы. Линейность предполагается по умолчанию.
   
5. 
   Множество состояний и начальное состояние системы задаётся в левой части исходной формы. Множество переходов – в правой. Над таблицей переходов имеются подсказки к заданию типов состояний и переходов: «Тип перехода: 0 – линейный, 1 – раствор, 2 – смесь» и т.д. согласно таблице на главной форме.
   

Кнопка «Запуск» предназначена для начала вычислений. Окна «Номер первого шага» и «Количество шагов» управлют счётчиком тактов. Например, можно начинать моделирование исторического процесса с некоторой даты в течение заданного числа лет. Кнопка «Графически» вызывает результирующую форму (Рис. 11.2.)

Н
астройка результирующей формы позволяет задавать цвет фона, крайние значения по осям графика, видимость графиков, цвет, толщину и тип линий. Есть возможность увеличивать части графика, для этого надо выделить увеличиваемую область левой кнопкой мыши из левого верхнего угла в правый нижний угол (). Чтобы отменить увеличение, надо выделить левой кнопкой мыши область в других направлениях (, , ). Результаты (графические и численные) можно сохранять или вызывать кнопками сохранения и вызова на панели управления результатами. Графики сохраняются в формате ACDSee 7.0 BMP Image. Численные результаты сохраняются в текстовом формате.

Для лучшего понимания рекомендуется самостоятельно и с помощью программы «Популяция» рассмотреть функции переходов на Рис.11.3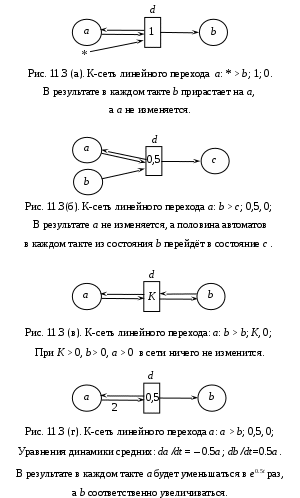

11.3. Типы переходов и задержки во времени

Ранее рассмотрено использование только простых переходов, изображённых на Рис.11.4 (а). Однако некоторые очевидные соображения и модификации значительно расширяют возможности моделирования. Добавленные виды переходов изображены на Рис.11.4 (б), (в), (г), (д). Это сохраняющий, удаляющий, остаточный и ингибиторный переходы. Итак, имеем.

1. 
   Простой переход, описанный правилом: «Состояние А переводит состояние В в состояние С с интенсивностью К по типу 0,1,2».
   
2. 
   Сохраняющий переход не изменяет число состояний в обеих входных позициях, что позволяет моделировать, например, гиперболический рост с обострением. Его правило «Состояния А и В не изменяются, но порождают новые состояния С с интенсивностью К по типу 3,4,5».
   
3. 
   Удаляющий переход извлекает маркеры из обеих входных позиций, как это делается в стандартной сети Петри. Его правило «Состояния А и В исчезают, и порождают новые состояния С с интенсивностью К по типу 6,7,8».
   
4. 
   Остаточный переход – модификация простого перехода такая, что изменяют свои состояния все те автоматы популяции, которые не изменили его в аналогичном простом переходе. Его правило «Состояние А переводит в состояние С те автоматы, которые находятся в состоянии В, но не перешли бы в состояние С при простом переходе. Интенсивность К; типы 9, 10, 11».
   
5. 
   Ингибиторный переход, дополнительный к простому: «Если в области действия нет состояния  А, то состояние В переходит в состояние С с интенсивностью К по типу 0, 1, 2». Здесь состояние А играет роль не инициатора, а ингибитора, запрещающего переход.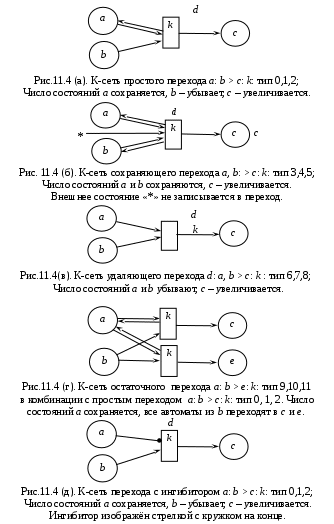
   

Все эти переходы могут работать линейно, в растворе, и в смеси. Соответствующие указания для программы даются в столбце таблицы переходов «Тип перехода». Линейные переходы имеют номера 0, 3, 6, 9; переходы в растворе – 1, 4, 7, 10; в смеси – 2, 5, 8, 11. Таким образом, имеется три типа и пять видов переходов, отличающихся способом подсчета интенсивностей. В результате получается следующая таблица возможных переходов в простых К-моделях.

Таблица 11.1.
Виды и типы переходов программы «Популяция»
Вид перехода	Тип перехода
	Линейный	Раствор	Смесь
Простой	0	1	2
Сохраняющий	3	4	5
Остаточный	6	7	8
Удаляющий	9	10	11
Ингибиторный	12	13	14

Кроме того, допустимы и временные запаздывания действующих состояний К-модели. Например, число повзрослевших особей в популяции определяется не наличным числом рождённых, а рождёнными некоторое время назад, определяемое возрастом взрослой особи. Соответствующие задержки указываются в столбцах Задержка 1 и Задержка 2 таблицы переходов.

Все эти возможности отражены в главной форме интерфейса программы «Популяция» (Рис.11.1).

11.4. Стохастическая корректность К-моделирования

1. Корректность перехода

В процессе изложения чаще всего неявно предполагалось, что интенсивности переходов p ≤ 1, т.е. являются вероятностями. Но бывают случаи, когда необходимо порождать несколько автоматов взамен удаляемого. Оказывается, что при p  1 число удаляемых автоматов может быть столь велико, что превышает их приращение от других переходов, и результат может оказаться отрицательным. Такой переход мы назовём некорректным.

Итак, необходимо учесть интенсивности p  1.

В простом случае запись перехода A, B > C, p, <0|1|2> читается так.

Состояние А переводит состояние B в состояние C с вероятностью (интенсивностью) pF(A,B). (Вспомним о договоренности обозначать одной буквой и состояние автомата, и число автоматов, находящихся в нём.)

Пусть дан переход A, B > C,p,<0|1|2> , т.е. «линейный», «раствор» или «смесь», соответственно. Обозначим через U= F(A,B) число автоматов, которые попали в область взаимодействия данного перехода. (Вспомним о договоренности обозначать одной буквой и состояние автомата, и число автоматов, находящихся в нём.) Число Uзависит от типа перехода и равно

U = min(A,B) или AB/N или AB/(A+B) (1)

для переходов типа «линейный», «раствор» и «смесь», соответственно. Число автоматов, которые действительно взаимодействуют при переходе, равно

V = p min(A,B) или pAB)/N или pAB/(A+B) (2)

для переходов типа «линейный», «раствор» или «смесь», соответственно.

При p < 1 именно V автоматов выбывают из входных состояний В (и А в удаляющем переходе) и переводятся в выходное состояние С. Нетрудно убедиться что число V всегда меньше исходных чисел А и В, поэтому эти манипуляции с автоматами не приведут к некорректности перехода.

При p  1 число V может оказаться больше А или В, и удаление такого числа автоматов из входных состояний приведёт к некорректности. А между тем, согласно здравому смыслу, удалять можно только существующие автоматы, а добавлять в выходное состояние можно сколько угодно, чтобы моделировать рост системы. Так мы и сделаем.

При p ≤ 1 будем удалять и переносить в другое состояние V автоматов.

При p  1 будем удалять только U, а добавлять все V автоматов.

Теперь допустимо p 1 без нарушения корректности перехода. Особую трудность составляет использование переходов типа «остаточный» и «ингибитор».

2. Типы переходов «остаточный» и «ингибитор»

Прежде всего, необходимо уточнить, что значат типы «остаточный» и «ингибитор». Словами их можно описать так.

3. Остаточный переход: A, B > C,p, <9|10|11>

Переход А,B > C с интенсивностью p = 1 совершают все те и только те автоматы, которые не сработали в соответствующем переходе

A, B > C,p,<0|1|2> .

Приp ≤ 1 число удалённых из В и перешедших в С автоматов равно p(В – V).

При p  1 из В удаляются только U автоматов, а в С добавляются все (В – U).

Это правило реализовано в программе «Популяция».

4. Ингибиторный переход: A, B > C, p, <12|13|14>

Переход B > C с интенсивностью pсовершают все те, и только те автоматы, которые не имеют в своей области взаимодействия ингибитора в состоянии A.

Число ингибиторов U вычисляется по формулам (1). В состояние C добавляются автоматы по формуле V = p(В – U), а удаление происходит так.

При p ≤ 1 из В удаляются p(В – V) сработавших автоматов.

При p  1 из В удаляются только (В – U) автоматов, свободных от ингибиторов.

5. Стохастическая корректность

Стохастическая корректность в методе динамики средних состоит в том, что

1. 
   ни один автомат не может участвовать в переходе или во взаимодействии более одного раза за такт моделирования и
   
2. 
   численность автоматов в любом состоянии не может быть менее 0.
   

5.1. Марковская модель

Для простой марковской модели ансамбля автономных вероятностных автоматов стохастическая корректность обеспечивается

1. 
   условием нормировки для строк стохастической матрицы переходов Q Σ_j = 1..n p_ij= 1 при любом i = const, где p_ij – вероятность перехода автомата из состояния i в состояниеj и
   
2. 
   тем, что автоматы в этой модели не взаимодействуют, а изменяют состояния сами по себе.
   

Преобразование вектора-строки Р вероятностей состояний происходит согласно уравнению

Р^(k+1) = Р^(k)Q

откуда с очевидностью следует стохастическая корректность. Корректность сохраняется и при использовании девиатора D = Q – Е в дифференциальном уравнении

dP/dt = Р D

и в уравнении для финальной вероятности автомата в ансамбле

Р_фин D = 0

Простота марковской модели ансамбля автоматов состоит ещё и в том, что стохастическая матрица Q не изменяется в процессе функционирования ансамбля.

5.2. Каузальная модель

При написании К-модели программист имеет дело не с ансамблем, а с системой автоматов, которые могут взаимодействовать между собой. При этом каждый автомат может быть упомянут не в одном, а в нескольких взаимодействиях. Чтобы обеспечить однократное взаимодействие каждого автомата следует придерживаться правила стохастической корректности для всех переходов

 P_ij ≤ 1 (3)

где P_ij – вероятность i-того перехода, изменяющего для j-тое состояние.

Нарушение стохастической корректности приведёт к тому, что одно и то же состояние, участвующее в разных переходах, может учитываться в такте неоднократно и, более того, число автоматов в некоторых состояниях станет меньше нуля. Интенсивности взаимодействий P_ij часто зависят от численности автоматов нелинейно и вычисляются автоматически. Программист не видит результата этих вычислений, т.е. не контролирует стохастическую корректность К-модели до её исполнения. Поэтому следует тщательно исследовать К-модель. Если корректность нарушается, то происходит либо быстрый рост численности популяции автоматов и переполнение разрядной сетки компьютера, либо в некоторых состояниях численность автоматов может оказаться меньше 0. В ранних вариантах программы «Популяция» эта ситуация (N_i< 0) обнаруживалась («контроль нуля») и насильственно присваивалось значение N_i = 0, что означало простое игнорирование стохастической некорректности. В последних вариантах программы контроль знака N_i можно отключать, и программист может обнаружить его отрицательное значение, а также сравнить результаты моделирования при включённом и выключенном «контроле нуля». В корректной К-модели результаты совпадут.

Неоднократный учёт одних и тех же автоматов во взаимодействиях одного такта может быть как во входных, так и в выходных состояниях переходов вида: А, В > C. Если неоднократно учитываются автоматы в состоянии А, то будут инициированы лишние взаимодействия, не обеспеченные численностью этого состояния. Если это В, то из этого состояния будут удалены лишние автоматы и их число может стать отрицательным. Для удаляющих переходов типа 6, 7, 8 отрицательным может стать и число автоматов в состоянии А. Состояние С является принимающим и может только переполняться из-за ложного учёта отсутствующих автоматов в состояниях А и В.

В любом случае проверка стохастической корректности должна быть сделана до составления моделирующей системы дифференциальных уравнений. К-модель позволяет получить численные результаты решения этой системы, минуя этап составления и анализа уравнений. Нарушения корректности К-модели можно обнаружить не только по указаниям программы, но и исходя из общей картины процесса. Она не должна противоречить здравому смыслу и интуиции исследователя.