Метод k-моделирования. МЕТОД К-моделирования. 3. каузальное моделирование популяций

• Название: 3. каузальное моделирование популяций
• Анкор: Метод k-моделирования
• Дата: 25.04.2022
• Размер: 2.74 Mb.
• Имя файла: МЕТОД К-моделирования.doc
• Тип: Документы; #496372
• страница: 10 из 12

12. Моделирование простых популяций

Модели простых популяций имеют множество полезных интерпретаций в различных предметных областях. Этот раздел посвящен освоению К-сетей и К-моделей на самых простых популяционных задачах: модели роста и модели мобилизации. Изложение сопровождается рисунками, полученными с помощью программы «Популяция». На этих рисунках (и далее везде) видна не только результирующая форма программы с графиками, но и её исходная форма с данными для представленных графиков. Более сложные модели читатель будет строить самостоятельно решая задачи, предлагаемые в конце книги.

Напомним для начала метод популяционного моделирования – математического и компьютерного моделирования сложных систем. Метод реализован для простых систем, где все переходы могут быть заданы фразами:

«Состояние i переводит состояние j в состояние k с интенсивностью K(i, j, k);тип».

Имея это в виду, мы договорились записывать переходы К-модели выражением вида

i: j > k; K;0|1|2

где, соответственно:i, j, k – имена состояний: действующего, исходного и результирующего, K – интенсивность перехода, а числа 0, 1 и 2 – альтернативные описания типа перехода: линейный, раствор и смесь.

Разумеется, допустимы совпадения имён i = j, i= k, j= k, i= j= k.

1. 
   При линейном переходе тройка (i: i > k) означает самостоятельный переход автомата из состояния i в состояние k.
   
2. 
   При нелинейном переходе, типа 1 или 2, тройка (i: i> k) означает, что автоматы из состояния i переходят в состояние k под воздействием других автоматов, находящихся в том же состоянии i.
   
3. 
   Интерпретация других случаев совпадений в тройке (i: i > k) понятна из предыдущего и может быть освоена экспериментально.
   
4. 
   Возможно рассмотрение открытых популяций, где присутствуют появление и гибель автоматов. Для этих целей введено внешнее состояние *. Рождение описывается вероятностью p(i: *> j), смерть – вероятностью p(i: j> *).
   

Далее мы рассмотрим некоторые простые модели.

12.1. Модели роста

Начинать изучение компьютерного моделирования сложных систем следует с простых К-моделей. Таковыми являются модели роста. Они содержат всего один переход и дают возможность детально изучить и понять как работает программа «Популяция». Показаны анализ и моделирование модели роста в её различных вариантах: линейный, раствор, смесь. Читатель может рассматривать этот раздел, как пример и инструкцию к решению задач популяционного моделирования.

Разнообразие моделей роста возникает, во-первых, из природы самих предметных областей, а, во-вторых, из разнообразия типов переходов. Между тем эти модели, как уже отмечалось, могут содержать интенсивности превышающие 1. Это создаёт трудности для их анализа и синтеза.

Для начала введём основные параметры роста. Пусть a_t и a_t+1 – число автоматов, находящихся в состоянии aв моменты дискретного времени t и t+1.

Показателем или скоростью роста назовём величину k, которая входит в определение процесса роста и не изменяется со временем.

Для линейного роста a_t+1 = a₀ + kt.

Для экспонециального роста a_t+1= a₀k^t илиa_t+1= a₀e^kt.

Ресурсом роста назовём некоторое множество автоматов в состоянии b, из которых создаются новые автоматы в состоянии a. Обычно ресурс роста ограничен.

12.1.1. Линейный рост с неограниченным ресурсом

М 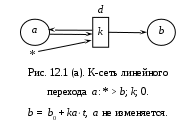одель линейного роста популяции с неограниченным ресурсом роста может быть представлена линейным переходом a:* > b;k, 0; где новые автоматы в состоянии b возникают из внешнего состояния «*», с постоянной скоростьюka, заданной числом родителей aи интенсивностью k, причём число родителей a не изменяется. Этот рост наблюдается при производстве каких-либо предметов (автоматов в состоянии b) одним и тем же производителем (автоматом в состоянии a), причём ни число производителей, ни их производительность не изменяются, а материалы для производства берутся из внешней среды в неограниченном количестве. К-сеть такого производства показана на Рис.12.1.(а).

Дифференциальное уравнение линейного роста имеет вид db/dt =ka, откуда следует линейное решение b = b₀ + kat, где ka – скорость роста. На Рис.12.1(б) представлены исходная и результирующая формы программы «Популяция», соответствующие линейному ростуb, приb₀ = 0, a = 2, k = 3. Здесь теоретическое и модельное поведение системы совпадают.





12.1.2. Линейный рост c ограниченным ресурсом

В реальных системах, всё равно биологических или экономических, ресурсы роста ограничены. Тогда новые элементы системы (c) делаются прои 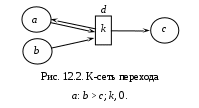зводителями (a) из автоматов ресура (b) со скоростью k, что записывается как линейный переход a:b > c;k, 0; aне изменяется, а все автоматы из состояния b перейдут в состояниеcсо скоростью k.

К-сеть показана на Рис.12.2.

Уравнения линейного ростаc с ограниченным ресурсом b выглядят так:

c = c₀ + kt∙min{a,b},

b = b₀ – min{kt∙min{a,b}, b }

Функция min появляется из-за того, что рост ограничен, как числом производителей, так и ресурсами, а расход ресурса не может быть больше, чем его остаток.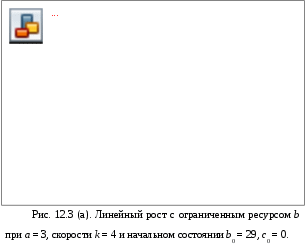


Рассмотрим случай, когда a < b. Тогда уравнения динамики имеют вид:

c = c₀ + kat

b = b₀ – min{kat, b}

Это значит, что скорость прироста определяется числом производителей и имеет место линейный рост со скоростью ka до тех пор, пока условие a₀ < b не будет нарушено, после чего скорость роста изменится и будет определяться уже ресурсом. 

График такого роста за 7 тактов при a =3, k = 4, b₀ = 29, c₀ = 0показан на Рис. 12.3 (а). Обратим внимание, что график убывания ресурса надламывается на втором такте, что говорит о том, что с этого момента рост ограничивается не числом производителей, а оставшимся ресурсом.

Кроме того, стационарное состояние c = 36 превышает b₀ = 29, т.е. то, что могло быть произведено. Это значит, что наша модель требует дополнительного рассмотрения. Дело в том, что скорость расхода ресурса меняется скачком именно в том месте, где нарушается условие a < b.

П
ри условии a > b уравнения динамики роста выглядят так:

c = c₀ + kbt

b = b₀ – min{kbt, b}

Согласно этим уравнениям скорость роста определяется ресурсом, причём на каждую единицу ресурса производится k единиц продукта. Показатель роста k изменил смысл, и если k >1, то такой режим может существовать только 1 такт. Вот почему в последнем такте роста нашей модели получается не точный и даже нелепый результат для стационарного режима.

Чтобы избежать такой ошибки ресурс следует задавать в количестве производимых предметов и он должен быть кратным скорости роста k. Осмысленный результат при a > b получается, еслиk < 1. Тогда в каждом такте продукта производится меньше наличного ресурса. График этого процесса дан на Рис. 12.3(б).

12.1.3. Нелинейный рост с ограниченным ресурсом.

Линейный рост с ограниченным ресурсом отражает ситуацию, когда ресурс роста находится «под руками» и его не надо искать или добывать. Если же это не так и ресурс надо искать, то рост описывается нелинейными переходами – раствор и смесь.

Рост в растворе происходит, когда продукт c находится в той же куче, что и ресурс, и производитель. Такова, например, ситуация когда все эти объекты представляют собой множество животных типа пауков «черная вдова», из которых надо выбрать подходящую пару (производитель-самка, ресурс-самец). В конце брачных игр чёрная вдова пожирает самца, поскольку он является одноразовым и больше не пригоден для воспроизводства. Подходящей интерпретацией является и популяция лососей, где родители погибают при нересте и превращаются в корм для потомства.

Рост в смеси происходит, когда продукт производства выводится за пределы популяции и не участвует в процессе производства. Ограничимся этим случаем.

Рост в смеси задаётся нелинейным переходом a:b > c;k, 2. К-сеть не отличается от случая линейного роста с ограниченным ресурсом. Единственное отличие – тип перехода. Ясно, что стационарный режим вырождается: b_стац = 0,c_стац = b₀ и c+b = b₀, a = a₀.

Таблица 12.1.
D		R
b	–1	kab/(a+b)
c	1

Дифференциальные уравнения динамики средних получаются из произведения DRсогласно таблице 12.1. и имеют вид

db/dt = – kab/(a+b)

dc/dt = kab/(a+b)

Н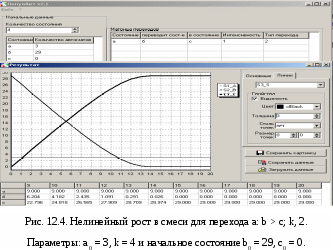
а Рис.12.4. показаны кривые нелинейного роста при тех же условиях, что и на Рис.12.3(а): a =3, k = 4, b₀ = 29, c₀ = 0. Но теперь процесс идёт без надломов, а стационарный режим соответствует начальным условиям.

12.1.4. Экспоненциальный рост с гибелью родителей

Экспоненциальный рост возникает, когда новые автоматы сами становятся родителями, а не приходят из внешнего мира. Этот рост экспоненциален и описывается, например, следующим линейным переходом.

a: a > a;k, 0; (12.1)

Здесь задано уничтожение всех aавтоматов-родителей (состояние a) и порождение ka новых автоматов в том же состоянии a при каждой реализации перехода. Таким образом происходит увеличение числа родителей в k раз в каждом такте. При этом сами родители погибают – делятся пополам Рис.12.5(а), что характерно для клеток и одноклеточных организмов.

С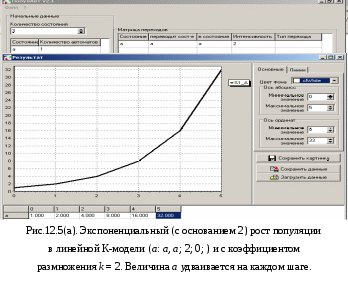
огласно (12.1) соответствующее дифференциальное уравнение, имеет вид

da/dt =ka (12.2)

а его решение – это уравнение экспоненциального роста a_t = a₀∙e^kt.

На первый взгляд это теоретическое решение не соответствует кривой роста, полученной методом моделирования и показанной на Рис.12.5(а) при a₀ = 1, k = 2. Однако, воспользовавшись теоремой масштабирования, мы можем домножить единицу времени на величину ln2/k, а за такую единицу времени величина a удвоится, как это показано на Рис.12.5(а).

Построим дискретную динамическую модель роста. В данном случае показатель роста равен k.При срабатывании перехода (12.1) происходит следующее преобразование величины a: a_t+1 = a_t– min{a_t, k a_t} + k a_t.

При k  1 имеем k a_t a_t, откуда a_t+1 = a_t= a₀,и никакого роста нет.

При k > 1 имеем a_t+1 = k a_t.

Эта рекуррентность порождает ряд значений a:

a₀ = a₀k⁰, a₁ = a₀k¹, a₂ = a₀k², a₃ = a₀k³,…, a_t = a₀k^t,…

При k = 2 получается удвоение числа a на каждом шаге процесса, что наглядно демонстрирует Рис.12.5(а).

П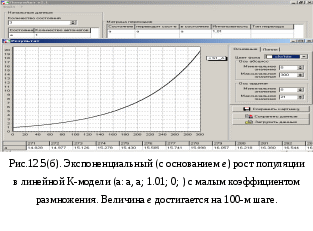
осмотрев на Рис.12.5(б), мы можем убедиться, что при k = 1,01 процесс роста происходит в хорошем соответствии с экспонентой по основаниюe. В данном случае коэффициент масштабирования практически равен ln2.

12.1.5. Экспоненциальный рост с сохранением родителей

Теперь можно рассмотреть и другие линейные модели экспоненциального роста. Если родители не погибают, но пополняются детьми, то подходит модель, заданная линейным переходом a: * > a;k, 0; В данном случае при извлечении новых автоматов из внешнего состояния «*» родители не гибнут. Так происходит рост численности популяций многоклеточных растений и животных. Процесс экспоненциального роста с коэффициентом k описывается рекуррентностью a_t+1 = a_t+ k a_t = (1+k)a_t, а она в свою очередь порождает последовательность:

a₀ = a₀(1+ k)⁰, a₁ = a₀ (1+ k)¹, a₂ = a₀(1+ k)²,…, a_t = a₀(1+ k)^t, … (12.3)

При подходящем масштабировании эта последовательность моделируется экспонентой с основанием eи показателем роста k

a = a₀e^kt

Таким образом, на Рис.12.5(б) изображён ещё и процесс роста без гибели родителей, но только при k= 0,01.

12.2. Модели мобилизации

Рассматривая модели роста мы не учитывали процессов вымирания особей. Такие процессы тоже протекают по тем же законам, что и рост, поэтому в моделях роста следует просто уменьшить скорость прироста k, взяв за её величину разность скоростей роста и умирания: k = k_роста – k_{вымирания} . При k_роста > k_{вымирания} всё будет как в моделях роста. При обратном соотношении k_роста < k_{вымирания} роль вымирающей популяции будет играть ресурс.

Простота модели мобилизации позволяет найти почти все её стационарные режимы аналитически. Анализ модели показывает, что даже в, казалось бы, тривиальном случае можно сделать совершенно неочевидные выводы. Далее будет показано, что популяция каннибалов, в которой убийство и смерть особи сопровождается поеданием её трупа, тоже может жить и размножаться, даже если вероятность убийства при встрече выше вероятности замены новым членом популяции. Таким образом, внутривидовая конкуренция не уничтожает популяцию, но, наоборот, может способствовать отбору наиболее сильных особей. Это, впрочем, один из известных тезисов Чарльза Дарвина.

Несмотря на простоту модели мобилизации, приходится немало потрудиться, чтобы рассмотреть её в различных вариантах. Оказалось, что и стационарное состояние не всегда можно найти, минуя переходной режим, как показало исследование линейной модели. Далее мы даже не пытаемся найти аналитическое решение уравнений динамики системы в переходных режимах. Для столь простой системы они, конечно, могут быть найдены. В большинстве же более сложных случаев поиск аналитических решений затруднителен, и если такие решения можно найти, то возникает проблема вычисления и представления соответствующего переходного поведения. Между тем во многих случаях вполне можно ограничиться теми графиками, которые рисует компьютер на основании модели.

Уравнения динамики средних для модели мобилизации были получены нами в п.10.1. для линейной популяции, при условии, что M – величина более высокого порядка малости по сравнению с M: M =о(M). Общий вид матричного уравнения динамики средних

dM/dt = D  R

Приравняв производную нулю, получим уравнение для стационарного режима:

D  R =0

Кроме этих уравнений для замкнутых популяций справедливо

Σ_i=1..nP_it = 1 или, что то же, Σ_i=1..nN_it = N

Для разных типов переходов вектор R будет различным в соответствии с формулами из п.п. 10.6. и 11.1. Для облегчения составления этих уравнений все случаи для комбинирования переходов в модели мобилизации сведены в таблицу 12.2.Как следует из Табл. 12.2. в модели мобилизации может быть 6 комбинаций типов переходов. Кроме того, некоторые из полученных уравнений будут следовать из других благодаря нормировке, а некоторые из независимых уравнений, те в которых есть функция min, расщепятся на 2 уравнения. Кроме того, используя теорему соразмерности, мы выразим все результаты анализа модели мобилизации через параметр v = q/p. Такое представление не зависит от конкретных значений qиp. Назовём его относительной формой.

Таблица 12.2.
Сводная таблица для получения уравнений динамики средних в модели мобилизации
D-оператор			Вектор R = {pj(Mt(*dj)); j =1,2} интенсивностей
D	d1	d2	0 – линейный	1 – раствор	2 – смесь
Ж	–1	1	pЖ	pЖ2 / (Ж + М)	pЖ
М	1	–1	q min{Ж, М}	qЖМ / (Ж + М)

12.2.1. Линейная модель мобилизации

Начнём с линейной модели мобилизации из п.10.4. Для стационарного режима имеем уравнение

pЖ = q min{Ж, N – Ж}

Расщепляя его, получаем два возможных режима (1) и (2).

(1) При Ж  N – Ж имеем стационарное уравнение pЖ = q(N – Ж) и, следовательно, Ж = N q/(p+ q) или P_Ж= q/(p+ q), а М = N p/(p+ q), причём Ж  М , что и следовало ожидать. В относительной форме

Ж = N v/(v+1)

М = N /(v+1)

(2) При N – Ж  Ж имеем стационарное уравнение pЖ = qЖ и, соотношение q = p, как некий рубеж между режимами (1) и (2).

В случае (2) получить решение для стационарного режима можно решив дифференциальное уравнение динамики средних при N – Ж  Ж и устремив время в бесконечность.

dЖ/dt = q Ж – pЖ= Ж(q – p)

Разделяя переменные имеем

dЖ/Ж = (q – p) dt

откуда получаем классическое экспоненциальное решение

Ж_t = Ж₀e^(q – p)t

Очевидно, что при t  и q < p популяция вымирает, а при q > p численность Ж растёт, и когда она достигает такого положения, что выполняется условие Ж  N – Ж, популяция стремится к стационарному состоянию уже в режиме (1) и достигает численности Ж = N v/( v+1). Но достигает ли популяция этого стационарного состояния? Разумеется! Функция Ж₀e^(q – p)t монотонно возрастает при q > p и ничто не мешает числу Ж_tрасти, пока не будет достигнуто условие режима (1), который ограничивает дальнейший рост Ж.

Наконец, на рубеже режимов (1) и (2), при q = p,т.е.v = 1, поведение популяции зависит от начальных условий. При Ж₀  М₀ достигается устойчивое состояние Ж = М = 0,5N . В противном случае, при Ж₀  М₀, сохраняется начальное состояние Ж_t = Ж₀, М_t = М₀.

На Рис.12.6 (а) и (б), 12.7 (а) и (б) представлены результаты моделирования простой популяции с линейными интенсивностями переходов, описанной в п. 10.1. Модель имеет начальное состояние Ж = 20, М = 80; и параметры: p = 0.3; q = 0.9, когда популяция живёт, и наоборот Ж = 80, М = 20, q = 0.3, p = 0.6, когда она вымирает. Число тактов моделирования Т = 10  100 в зависимости от типа модели. Впрочем, эти параметры меняются от модели к модели для наглядности. Все изменения параметров описаны в легендах к рисункам.

Нетрудно убедиться что в стационарном режиме модель подтверждает теоретические расчеты. Однако переходной режим на Рис.12.6(а) совсем не похож на экспоненту и представляет собой ломанную кривую.

Дело в том, что при выбранном варианте параметров p + q = 1.2 > 1. При заданных начальных значениях Ж =20, М =80 приращения Ж и М в первых тактах настолько велики, что не удовлетворяют условию малости М. Поэтому величины Ж и М «проскакивают» стационарные значения, а их графики «ломаются» чтобы вернуться на стационарный режим. Это значит, что дифференциальные уравнения неприменимы в переходном режиме такой системы, хотя стационарное состояние сохраняется. Иная картина представлена на Рис.12.6(б).

В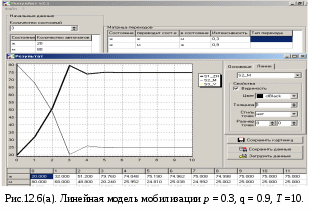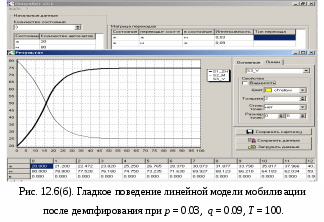

математической модели сглаживание динамикипопуляцииполучается одновременным уменьшением интенсивностей переходов, т.е. уменьшением шага вычислений и более медленным приближением к стационарному состоянию. Согласно теореме масштабирования поведение системы в стационарном режиме от этого не изменится, но переход в стационарный режим становится гладким. Результат такого демпфирования как раз и показан на Рис.12.6(б), где интенсивности переходов уменьшены на порядок: p = 0.03, а q = 0.09, а число тактов моделирования увеличено до 100.

Реальные системы могут иметь как раз такие параметры p и q , что переходный режим не будет гладким, а будет чем-то вроде того, что показано на Рис.12.6(а). Такое явление в теории управления называется перерегулирование. Для ликвидации перерегулирования в механических системах управления вводится демпфер – устройство снижающее реакцию системы управления на входное воздействие. В электронных системах управления также вводится искусственное ослабление реакции выхода на входной сигнал.

Н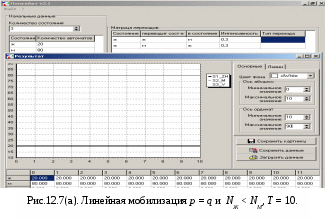
а Рис.12.7(а) показано стационарное состояние популяции на рубеже между режимами выживания и вымирания. На Рис.12.7(б) показано вымирание популяции или, если угодно, крах мобилизации из-за массового бегства призывников.

1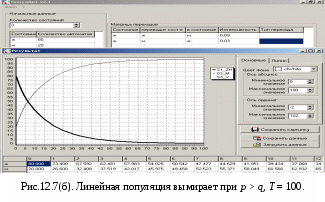
2.2.2. Нелинейные модели мобилизации

Рассмотрим теперь ту же популяцию, живущую в растворе из множества мест (М) и множества особей (Ж). Пусть теперь оба перехода нелинейные типа раствор. К‑сеть для этого раствора представлена на Рис.12.8.

Здесь по-прежнему, p – вероятность гибели, q – вероятность восстановления особей. В данном случае переход d₁ означает не естественную смерть, а внутривидовую конкуренцию особей. Если две живые особи встречаются, то одна из них с вероятностью p убьет другую и съест. Более того, вся экологическая ниша нашей популяции занята и никаких источников пищи, кроме биомассы самих особей и той энергии, которую даёт занимаемое место, больше нет. При этом место может прокормить своего хозяина, но для размножения необходимо убить и съесть своего собрата по виду. Такой способ питания «с места» и убитыми особями своего вида называется каннибализм или адельфофагия. На первый взгляд адельфофагия – биологический нонсенс. Но так ли это?

У 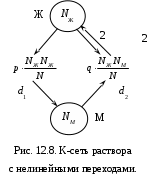равнения динамики средних для раствора имеют следующий вид: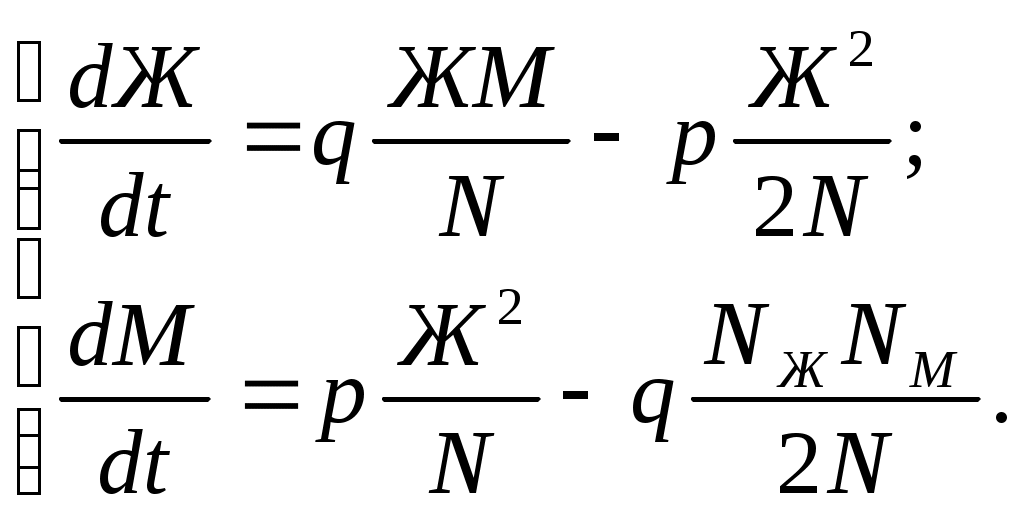



Так как популяция у нас замкнутая и Ж + М = N,получается одно уравнение для Ж.

Найдем стационарный режим, при тех же начальных значениях Ж = 20, М = 80 с параметрами p = 0.03, q = 0.09.

Имеем:



Откуда



М = 14,286.

Р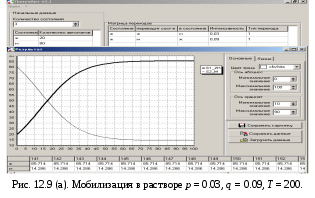
езультат моделирования иллюстрирует Рис.12.9(а). Он отличается от линейного варианта с теми же параметрами и начальными условиями другими стационарными значениями Ж и М и значительно меньшей скоростью изменений, так что для достижения стационарного режима потребовалось не 10 и не 100, а 200 тактов. Всё это неудивительно.

Но вот рисунок Рис.12.9(б) демонстрирует качественно иное поведение нелинейной популяции. При тех же начальных условиях линейная модель приходит к полному вымиранию живых организмов, а нелинейная к стационарному состоянию, в котором живые и мёртвые организмы остаются в достаточном количестве в соотношении Ж/М = 40/60.

Нелинейная популяция выживает при внутривидовой конкуренции, даже если интенсивность убийства намного больше чем интенсивность восстановления. Объяснение этого факта состоит в том, что при низкой численности живых особей они редко встречаются и перестают конкурировать. Найти и убить соперника в растворе, где соперников мало, настолько маловероятно, что жертвы успевают размножаться. По этой же причине, вытеснение генов, ослабляющих особь-носителя в конкуренции, не может быть завершено до конца. «Слабаки» всегда будут присутствовать в популяции.

В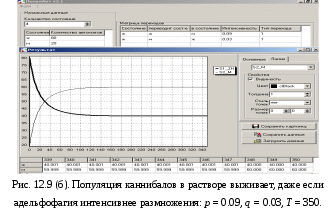
ообще, нелинейные системы ведут себя «мягче» линейных в отношении исчезающих состояний. С другой стороны их поведение гораздо сложнее и интереснее линейного случая. Так в известной модели "хищник‑жертва" возникают колебания численности хищников и жертв, сдвинутые по фазе. Рост числа жертв ведёт к росту числа хищников и снижению числа жертв, а вслед за тем и к частичному вымиранию хищников, что, в свою очередь даёт возможность размножения жертв и т.д. Модель хищник-жертва оставляется читателю как задача для самостоятельного исследования.

12.2.3. Мобилизация со смешанными переходами

У 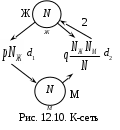страним конкуренцию заменив переход d₁ на линейный. Пусть особи умирают сами по себе с вероятностью p. (Рис.12.10.) Уравнения динамики средних при N =Ж + М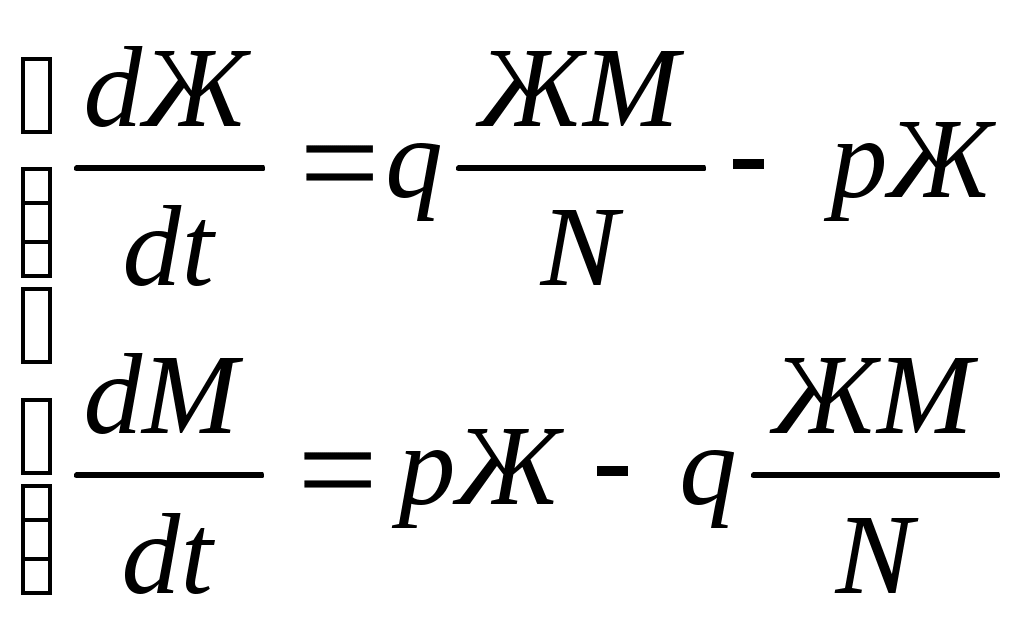



Решение системы дано в Таблице 12.3.