Метод k-моделирования. МЕТОД К-моделирования. 3. каузальное моделирование популяций

• Название: 3. каузальное моделирование популяций
• Анкор: Метод k-моделирования
• Дата: 25.04.2022
• Размер: 2.74 Mb.
• Имя файла: МЕТОД К-моделирования.doc
• Тип: Документы; #496372
• страница: 7 из 12

10. Динамические модели популяций

Как и сеть Петри, К‑сеть может использоваться для моделирования сложных систем, состоящих из множества взаимодействующих элементов – популяций. Абстрагируясь от природы популяции, будем называть её элементы автоматами. А саму динамическую модель, построенную на основе К-сети, будем называть К-моделью. Этот последний термин синоним термину К-сеть, но подчёркивает динамический характер и модельную функцию К-сети.

10.1. К‑модель мобилизации

Проще всего пояснить основные идеи популяционного моделирования на примере. Рассмотрим, например, замкнутую «популяцию», которую представим как популяцию автоматов-особей с двумя состояниями Ж (живая) и М ( мёртвое место). Вероятность гибели особи и освобождения места (перехода из Ж в М) в течение одного такта равна p. Живая особь, может найти одно место и разделиться на двух живых или, иначе говоря, оживить мёртвое место. Вероятность этого события в течение одного такта равна q. Временем на поглощение и деление можно пренебречь по сравнению со временем поиска места. В популяции определены два перехода: гибель, независимая от состояния популяции, и восстановление, возможное только при наличии одной живой особи и одного места. С целью экономии обозначений будем иногда записывать функцию времени X(t)в виде X_t или вообще не указывать этот индекс без необходимости. В этих обозначениях начальное состояние популяции: M₀ = {Ж₀, М₀}.

Предложенная К-модель имеет массу различных интерпретаций. Это и модель заселения мест (М) экологической ниши живыми (Ж) организмами, и модель замены отказавших узлов системы (М) исправными узлами (Ж), это и модель спасения раненых на поле боя живыми бойцами, это, наконец, модель мобилизации призывников (М) теми, кто уже призван в армию (Ж), причём призывники активно избегают призыва – «умирают». Последняя интерпретация позволяет называть описанную популяцию моделью мобилизации, как это принято в экономической литературе. Автоматы этой модели мы будем называть особями.

Зададим, для начала, модель мобилизации с линейными интенсивностями переходов. К‑сеть для модели мобилизации показана на Рис. 10.1.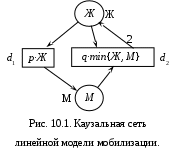

Описание этой популяции, пригодное для ввода в компьютер:

Ж = Ж₀, М = М₀;

Ж> М: pЖ, линейно;

Ж, М > 2Ж: q∙min{Ж, М}, линейно.

Здесь запятая « , » – разделитель между элементами множеств. Знак « > » – разделитель между входами и выходами перехода. Знак « : » – разделитель между переходом и его интенсивностью. Знак « ; » – разделитель между целостными частями описания. Выражения pЖ и q∙min{Ж, М} – интенсивности, т.е. среднее число особей, погибших и восстановленных в течение одного такта, соответственно. Точка « . » завершает описание.

Интерпретация предложенного описания популяции зависит от единицы времени. Если единица времени достаточно мала, то p << 1 и q << 1 – вероятности переходов в течение такта, а p∙Ж и q∙min{Ж, М} – среднее число автоматов, изменяющих состояние за такт. Если единица времени велика, то p и q – интенсивности переходов одного автомата, а величины p∙Ж или q∙min{Ж, М} – это интенсивности допустимых переходов на всём множестве автоматов, готовых к переходу. В первом случае мы имеем уже знакомую модель вероятностных автоматов, во втором – возможны осложнения.

10.2. Классификация К-моделей

К-модели классифицируются по нескольким критериям.

Во-первых, следует выделить линейные и нелинейные модели взаимодействий. Эти модели, как было указано выше, отличаются видом функций интенсивностей переходов p_j(M_t(*d_j)).

Во-вторых, о сложности модели можно судить по числу состояний и автоматов, участвующих в одном акте взаимодействия и в переходе.

В-третьих, К-модели различаются по составу моделируемой популяции.

Все эти различия решающим образом влияют на моделирование популяций и, следовательно, требуют более содержательного описания.

10.2.1. Линейные и нелинейные взаимодействия

Линейные взаимодействия таковы, что интенсивности p_j(M_t(*d_j)) пропорциональны минимальным маркерам N_it в M_t(*d_j). Линейные модели адекватны в тех случаях, когда интенсивность перехода является имманентным свойством каждого отдельного автомата. Так в нашей гипотетической популяции способность восстанавливать мертвую особь присуща только части особей, находящихся в состоянии Ж, но если уж эта способность есть, то она реализуется, и эта реализация единственна в данном такте.

Иной способ понимания свойства линейности К-модели – положить, что взаимодействия между автоматами являются дальнодействующими, т.е. взаимосвязи (отношение соседства) между элементами системы можно представить полным графом. Рассмотрим, например, боевое столкновение двух воюющих сторон 1 и 2 в чистом поле, когда каждый «живой» боец видит каждого «живого» противника и может поразить его из дальнобойной винтовки, т.е. перевести его в состояние «мёртвый». Пусть N₁ и N₂ – численности «живых» с обеих воюющих сторон в данный момент времени, p и q – вероятности попадания в противника у стрелков соответствующих сторон, N_M – численность «мёртвых». Общая численность мест, занятых всеми живыми и мёртвыми солдатами, равна N=N₁ + N₂ + N_M.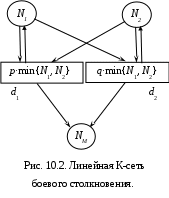

Линейная К-сеть такого столкновения показана на Рис. 10.2. В ней два перехода d₁, d₂ и три позиции1, 2, M.

Маркировка M_t этой К-сети задаётся тройкой {N₁, N₂, N_M}, а интенсивности уничтожения противников (число врагов, убитых каждой стороной в каждом такте времени) вычисляются по следующим формулам:

p₁(M_t(*d₁)) =p₁(N₁, N₂)= p∙min{N₁, N₂}

p₂(M_t(*d₂)) = p₂(N₁, N₂) = q∙min{N₁, N₂}

где: p₁(N₁, N₂) – интенсивность перехода d₁ из N₂ в M, p₂(N₁, N₂) – интенсивность перехода d₂ из N₁ в M. Член min{N₁, N₂} отражает тот очевидный факт, что число одновременных выстрелов не может превышать ни числа видимых противников, ни числа стреляющих. Этот член может появиться в сети автоматически. Таким образом, чтобы задать линейные переходы, достаточно указать только их вероятности (в данном случае p и q).

Нелинейные популяции таковы, что p_j(M_t(*d_j)) зависит от степеней и произведений маркировок N_it из M_t(*d_j). Нелинейная модель адекватна, если интенсивность перехода пропорциональна вероятности возможных благоприятных сочетаний, причём все эти сочетания и соответствующие переходы могут быть реализованы в одном такте с заданной вероятностью. Так, в рассмотренной модели мобилизации следовало бы учесть вероятность «встречи» одной живой и одной мёртвой особи, точнее попадания мёртвой особи в поле зрения живой. Такая вероятность будет пропорциональна произведению плотностей взаимодействующих автоматов. Тогда интенсивность восстановления будет пропорциональна величине Ж∙М/N.

По аналогии с линейной популяцией, можно представить нелинейный случай, как близкодействующее взаимодействие автоматов. При этом взаимодействие происходит на некотором конечном расстоянии. Это расстояние можно задать коэффициентом, имеющим смысл эффективного сечения или зоны, в которой только и возможно взаимодействие. Будем называть эту зону областью действия для действующего автомата и областью восприимчивости для автомата, подвергающегося воздействию. В случае взаимодействия двух автоматов область действия и область восприимчивости совпадают и могут называться просто областью взаимодействия.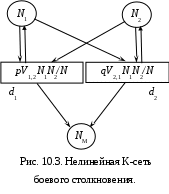

Так в модели боевого столкновения следует полагать, что оружие, (например, меч или копьё) не обладает бесконечной дальностью поражения. Для обеих воюющих сторон дальность поражения, т.е. область действия, может быть различной и задаётся коэффициентами V_1,2 и V_2,1. Теперь для того, чтобы задать интенсивность взаимодействия, мало задать вероятности p и q. Необходимо домножить их на коэффициенты V_1,2 и V_2,1 и на значение N₁N₂/N, которое задаёт интенсивность встречи двух близкодействующих бойцов.

Величину N₁N₂/N можно получить автоматически, а значения коэффициентов pV_1,2 и qV_2,1 следует задать «руками». Ясно, что эти задаваемые величины теперь уже не обязаны быть вероятностями, и могут превышать единицу. Более того, и итоговые интенсивности взаимодействий pV_1,2N₁N₂/N и qV_2,1N₁N₂/N могут превышать единицу, т.е. не быть вероятностями. Этот случай соответствует порождению новых автоматов в системе. Нелинейная К-сеть боевого столкновения показана на Рис. 10.3.

10.2.2. Простые популяции

Сложность популяции задаётся числом взаимодействующих автоматов в каждом переходе. Полезно выделить более простые случаи.

Простые популяции таковы, что взаимодействуют только пары автоматов. Каждый переход инициируется одним или двумя состояниями, а простой D‑оператор состоит из нулей и единиц, может быть с разными знаками. В столбцах матрицы D находится не более двух единиц, как в примере с «особями».

Простейшая популяция – это простая линейная популяция.

Автоматная популяция – это простейшая популяция, в которой все элементы являются автономными вероятностными автоматами. Этот случай относится к ранее развитому методу динамики средних.

10.3. Динамика К-сети

Граф, который мы назвали К-сетью, – это статическая модель популяции автоматов. Она задаёт только причинно следственные связи между элементами системы автоматов. Динамическая модель популяции – К-модель – определяется функционированием К-сети. Функционирование К‑сети подобно несущей сети Петри с учётом интенсивностей переходов, а именно: переход d_j срабатывает только тогда, когда маркировка его входа такова, что M(*d_j) ≥ In(d_j). В нашем примере: Ж  ≥ 1 и min{Ж, М} ≥ 1. При срабатывании перехода маркировка на его входе уменьшается, а на выходе увеличивается в соответствии с *d_j и d_j*. В нашем примере переход Ж > М: p∙Ж уменьшает маркировку Ж позиции Ж и увеличивает маркировку М позиции М на p∙Ж, а переход Ж, М > 2Ж: q∙min{Ж, М} уменьшает Ж на q∙min{Ж, М}, уменьшает М на q∙min{Ж, М} и увеличивает Ж на 2q∙min{Ж, М}.

Пусть N_t =   – численность популяции в момент t, P_it = N_it/N_t – доля автоматов, находящихся в момент t в состоянии N_i. При N_t  ∞ это вероятность пребывания автомата в i‑том состоянии. Вектор‑функция P_t = {P_it | i = 1, …, n} задаёт динамику популяции в среднем или её поведение.

10.4. Уравнения динамики средних для замкнутой популяции

Пусть R = d₁, d₂, d₃, d₄, …, d_s – допустимая последовательность переходов К‑сети. Рассмотрим только тот случай, когда сеть такова, что каждый из её переходов неоднократно найдётся в последовательности Rпри достаточно длительном наблюдении. Вектор R длины m, в котором j‑тая компонента это число вхождений перехода d_j в последовательностьR, называется характеристикой последовательности Rили характеристикой динамики К-сети. Взяв период наблюдения К-сети за единицу времени, мы отождествим характеристикуR и вектор‑функцию R = {p_j(M_t(*d_j)) | j = 1,…, m} интенсивностей переходов. Пусть теперь R – вектор‑столбец длины m, характеризующий динамику (число переходов) К-сети за единичное время. Тогда вектор‑столбец Rt – характеристика динамики за время t.

При описании К-моделей общего вида мы использовали обозначение N_i для числа автоматов, находящихся в состоянии i. Чтобы не загромождать запись уравнений буквой N, её можно опускать, и тогда имя i состояния будет обозначать и число автоматов в этом состоянии, как это обычно принято в элементарной алгебре. С той же целью экономии обозначений мы записываем функцию времени X(t)в виде X_t .

Функции In иOut для К-сети задаются (nm)‑матрицами инциденций, где строкам соответствуют позиции сети (кроме внешней), а столбцам – переходы. Элементы этих матриц значения k_ijи k_ji, соответственно. Вектор столбец R­ задает интенсивности переходов и его длинаравна длине строки матриц In иOut. Наглядно это демонстрирует Таблица 10.1.

Таблица 10.1.

Матричное описание К‑сети для популяции автоматов-особей

In

d1

d2

Out

d1

d2

D

d1

d2

R = {pj(Mt(*dj)) | j =1,2}

Ж

1

1

Ж

0

2

Ж

–1

1

p∙Ж

М

0

1

М

1

0

М

1

–1

q∙min{Ж, М}

Динамика К-сети (К-модель) задаётся матричным уравнением К‑сети, аналогичным фундаментальному уравнению сети Петри:

M = Out  Rt – In Rt = (Out – In) Rt = D  Rt

где:

Out – In = D – оператор изменения маркировки сети или D‑оператор (от Derivative – производная);

M – вектор‑столбец длины n – изменение маркировки сети при срабатывании любой допустимой последовательности переходов с характеристикой Rt;

 – матричное умножение.

Устремим t к нулю, и заменим его на дифференциал dt. Тогда и M станет величиной более высокого порядка малости по отношению к M: M =о(M) и её тоже можно заменить на dM. Теперь можно перейти к дифференциальному виду, и записать дифференциальное уравнение динамики средних для К‑сети в векторном виде:

dM/dt = D  R

Приравняв производную нулю, получим уравнение для стационарного режима:

D  R =0

Кроме этих уравнений для замкнутых популяций справедлива нормировка

Σ_i=1..nP_it = 1 или, что то же, Σ_i=1..nN_it = N

Особенностью полученных линейных систем является тот факт, что уравнения в них могут быть расщепляемыми.

В нашем примере с популяцией особей имеем систему

dЖ/dt = q∙min{Ж, М} – p∙Ж

dМ/dt = p∙Ж – q∙min{Ж, М}

где каждое из уравнений расщепляется на два различных уравнения, действующих в зависимости от соотношения значений Ж и М. Поскольку популяция замкнута и N = Ж +М = const, эти два дифференциальных уравнения сводятся к одному

dЖ/dt = q∙min{Ж, N – Ж} – pЖ,

которое расщепляется на два уравнения и интегрируется.

Если в К‑сети найдётся m переходов, меняющих интенсивности как функция min{x, y}, то система из m уравнений даст О(2^m) вариантов систем в соответствии с различными наборами значений функций min{x, y}. При этом популяция может иметь несколько различных стационарных состояний.

Анализ этой модели будет проведён далее в п.12 в связи с анализом различных вариантов модели мобилизации.

10.5. Растворы и смеси

До сих пор мы задавали интенсивности переходов непосредственно или, как говорят, «руками». Попытаемся автоматизировать подсчёт интенсивностей переходов в К-моделях популяций. Будем полагать, что моделируемые популяции сильно перемешаны, т.е. за время моделирования каждый автомат может оказаться в любом месте с одинаковой вероятностью независимо от расстояния до него.

Что касается линейных взаимодействий, то формулы для интенсивностей переходов, представленные в п.п. 10.1 и 10.2.1 в комментариях не нуждаются и их вычисление всегда можно провести автоматически. Однако нелинейные взаимодействия допускают различные интерпретации и способы вычисления интенсивностей. Для простоты рассмотрим только простые нелинейные популяции, поскольку результаты легко обобщаются на нелинейные популяции общего вида. Выделим два типа популяций: раствор и смесь.

Популяция типа раствор представляет собой равномерное размещение взаимодействующих автоматов во множестве мощности N мест, большинство из которых – места, не содержащие взаимодействующих автоматов. Примерами таких популяций в биологии являются популяция белых медведей и птиц, которые не собираются в одном месте для воспроизводства. Проблемой таких популяций является низкая вероятность встречи, если ареал расселения велик по сравнению с численностью популяции. Вероятность встречи самца и самки может оказаться меньше чем вероятность смерти отдельной особи, и популяция вымирает из-за малой численности в большом ареале расселения.

Популяция типа смесь собирается для взаимодействия в ограниченной области как, например, птичьи базары, пассажиры в трамвае или покупатели в магазине. Так что вероятность взаимодействия данной пары не зависит от общего числа мест, а зависит только от количества автоматов собравшихся вместе для взаимодействий.

Ясно, что в сложных популяциях различные взаимодействия могут происходить по-разному: и линейно, и как в растворе, и как в смеси. Поэтому тип популяции может быть (и чаще всего бывает) смешанным, а характеристики: линейный, раствор и смесь относятся далее не ко всей популяции, а отдельно к каждому взаимодействию. Рассмотрим интенсивности переходов для различных типов взаимодействий. Для экономии слов будем употреблять термины раствор и смесь достаточно вольно. Например, будем говорить о взаимодействиях или переходах в растворе или в смеси.

Пусть тройка (i,j,k)обозначает переход автомата из состояния j в состояние k под воздействием автомата, находящегося в состоянииi, а p(i,j,k) – вероятность такого перехода. При этом число автоматов в состоянииi не изменяется, если i k. Будем полагать, что каждый автомат занимает ровно одно место в пространстве, где «живёт» популяция. Общее число таких мест равно N. При этом часть мест может быть пустой, т.е. популяция как бы «растворена» во множестве мощности N. Пусть теперь:

N_i – число автоматов в состоянии i;

N_ijk– интенсивность перехода(i,j,k),т.е. число автоматов, совершающих этот переход в каждом такте моделирования;

V_ij – область взаимодействия для перехода (i,j,k)– число мест в окрестности состояния i (илиj), в которые должны попасть оба автомата i и j, чтобы взаимодействие состоялось. Ясно, что области взаимодействия состояний i и j одинаковы, т.е.V_ij=V_ji. Следует так же иметь в виду, что области V_ij должны быть порядка одного места:V_ij  1, чтобы можно было пренебречь их пересечениями.

K(i,j,k)= p(i,j,k)V_ij – интенсивность перехода (i,j,k) для одной пары автоматов, попавших в область взаимодействия размера V_ij в состоянияхi и j.

Наша задача состоит в вычислении общей интенсивности перехода N_ijk для различных типов взаимодействия. В растворе плотность автоматов в состоянииj равна p_j = N_j /N, общий объём области взаимодействия равен V_ij min{N_i, N_j}. Пусть N_i= min{N_i, N_j}. Тогда число взаимодействующих автоматов равно N_ijk = V_ij min{N_i,N_j}×p_j = V_ijN_iN_j/N.

Отсюда следует, что для взаимодействия в растворе

N_ijk = p(i,j,k)∙V_ijN_iN_j /N = K(i,j,k)∙N_iN_j /N.

Точно те же рассуждения для взаимодействия в смеси приводят к выводу, что значение N, следует заменить на сумму(N_i+ N_j) поскольку в этом случае оба взаимодействующих множества автоматов «растворены друг в друге», а прочие автоматы роли не играют. Так для заражения гриппом больные и здоровые люди должны встречаться в каком-нибудь тесном месте, например в офисе, чтобы обменяться вирусом, а прочие обстоятельства – размер города или всей страны – роли не играют. Итак, для компактного взаимодействия

N_ijk = p(i,j,k)∙V_ijN_iN_j/(N_i+N_j) = K(i,j,k)∙N_iN_j/(N_i+N_j)

Другой способ получения этих же формул состоит в следующем. Коль скоро p_j = N_j /N – плотность состояния j в объёме N, то вероятность встречи двух состояний i и j в области взаимодействия V_ij, близкой к единице объёма равна N_iN_j/N². Тогда во всём объёме N состоится N_iN_j/Nвстреч, вероятность события-перехода в момент встречи равна p(i,j,k), а интенсивность перехода K(i,j,k) = p(i,j,k)V_ij, где V_ij – коэффициент, учитывающий, что взаимодействие происходит на некотором расстоянии между автоматами. Интенсивность перехода K(i,i,k) может превышать 1, и обычно она является эмпирическим коэффициентом. Очевидно, что величина K(i,j,k) для одной пары автоматов – это параметр взаимодействия, который следует задать «руками», а остальная часть формулы для интенсивности перехода может быть вычислена автоматически, если указать тип перехода.

10.6. Инвариантность К-моделей

Поведение популяции мы определили как вектор функцию P_t = {P_it | i = 1, …, n} вероятностей состояний, зависящую от времени. Очевидно, что поведение любой популяции не зависит ни от единиц измерения времени, ни от её точной численности. Поэтому будем говорить, что две вектор‑функции P_t и P`_t инвариантны и задают одно и то же поведение, если одна из них переходит в другую при смене масштаба времени и/или численности. Такие преобразования масштабов назовём масштабированием. Соответственно, модели, порождающие инвариантное поведение эквивалентны. Рассмотрим условия, при которых такая инвариантность возможна.

Обратим внимание, что матрица D имеет как положительные, так и отрицательные элементы. Положительные элементы задают прирост (+N_j)числа автоматов в состоянии j. Отрицательные элементы матрицы D задают убыль числа автоматов (–N_j) в этом состоянии. Мы предполагали ранее, что эти приращения меньше чем общее число автоматов: |N_j| << N_j, для всех j = 1, …, m, так что этим самым обеспечивается достаточная точность вычислений. При этом графики функций в переходном режиме достаточно гладкие, т.е. не имеют точек излома и смены направления роста N_jt для всех j = 1, …, m. Невнятный термин «достаточно» станет понятен при анализе конкретных моделей популяций. Пока предположим, что для данной К-модели существует максимальный вектор R_max = {p_j^max(M_t (*d_j)) | j = 1, …, m} интенсивностей переходов, такой, что выполняется |N_i| << N_i и обеспечивается достаточная точность вычислений и гладкость графиков N_jt для всех j = 1, …, m.

К-модели имеют следующие свойства, которые можно сформулировать как теоремы.

10.6.1. Масштабируемость.

Теорема масштабируемости. К-модели масштабируемы. Это значит, что:

1. 
   Вектор‑функцию R_max интенсивностей переходов можно умножать на число 0 < r< 1без изменения стационарного поведения популяции.
   
2. 
   Компоненты вектора M₀ можно одновременно умножать на произвольное действительное число s > 0 без изменения стационарного поведения популяции.
   

10.6.2. Нормировка.

Теорема нормировки. Если в замкнутой К-модели сумма всех (кроме N₀) компонент вектора M_tравна 1, то M_t= P_t – вектор вероятностей её собственных состояний.

Эти утверждения справедливы в силу исходного предположения, что все потоки событий в системе простейшие, т.е. плотность вероятности события и интенсивность потока событий связывает соотношение dp = λdt. Другим, уже чисто математическим, основанием для утверждений об инвариантности и вероятностях состояний является тот факт, что изменение масштаба времени или численности популяции эквивалентно умножению матриц In,Out,D, R и M на одно и то же число, что не меняет характер решения соответствующих уравнений (кроме, разумеется, масштабов).

Вектор-функция R = {p_j(M_t(*d_j)) | j =1, …, m} интенсивностей переходов может быть проинтерпретирована как вектор вероятностей переходов, только если такт t и, соответственно, компоненты вектора R достаточно малы. В этом случае модель популяции допускает компьютерное моделирование методом t, где за величину приращения времени t берётся один такт, и каждое новое значение N_j(t) вычисляется потактно. Это ничто иное, как численное интегрирование дифференциальных уравнений динамики средних для популяции. Такая модель называется синхронной.

Масштабируемость имеет место только для стационарного состояния К-модели. Дело в том, что если потактные изменения N_j(t) будут слишком велики, то возникнет эффект малой точности вычислений в переходном режиме. В результате процесс моделирования может «проскакивать» малые изменения N_j(t). Модель станет слишком грубой и это исказит график функции N_j (t), нарушит его гладкость.