Метод k-моделирования. МЕТОД К-моделирования. 3. каузальное моделирование популяций

• Название: 3. каузальное моделирование популяций
• Анкор: Метод k-моделирования
• Дата: 25.04.2022
• Размер: 2.74 Mb.
• Имя файла: МЕТОД К-моделирования.doc
• Тип: Документы; #496372
• страница: 3 из 12

ГЛАВА 2. МАРКОВСКИЕ СИСТЕМЫ

4. Марковские модели

4.1. Необходимые понятия теории вероятностей

Для понимания последующего материала главы необходимо вспомнить некоторые элементы теории вероятностей.

Некоторое событие называется случайным по отношению к данному опыту, если при осуществлении этого опыта оно может наступить, а может и не наступить.

Пусть А – случайное событие по отношению к некоторому опыту. Пусть данный опыт произведен N раз и при этом событие А наступило в N_A случаях, соотношение



назовем частотой наступления события А в рассматриваемой серии опытов.

Частота большинства случайных событий обладает свойством устойчивости, т.е. при увеличении числа опытов частота стабилизируется, приближаясь к некоторой постоянной величине.

Вероятность случайного события – это связанное с данным событием постоянное число, к которому стремится частота наступления этого события в длинных сериях опытов.

Предложенное ранее определение вероятности обычно называют «статистическим определением» или «частотным определением», такое определение интуитивно понятно, но строгую теорию на основе такого определения не построить. Поэтому рассмотрим аксиоматический подход, предложенный А.Н. Колмогоровым, более типичный для математических дисциплин.

Пусть задано некоторое множество  – множество элементарных событий. Пусть S – совокупность событий,где S определяется, как непустая совокупность подмножеств множества .

Аксиомы событий (требования к совокупности S):

1. 
   Если множества A₁, A₂, … (в конечном или счетном числе) суть события, то их объединение A₁ + A₂+ … тоже является событием.
   
2. 
   Если множество A является событием, то его дополнение (до ) также является событием.
   

Два события Aи B, не имеющие (как два подмножества) общих элементов, называются несовместными.

Аксиомы вероятностей:

1. 
   Вероятность события A– это неотрицательное число p(A)  (0  p(A)  1), поставленое в соответствие каждому событию A.
   
2. 
   Аксиома счетной аддитивности. Если события A₁, A₂, … попарно несовместны, то p(A₁ + A₂ + …) = p(A₁) + p(A₂) + …
   

2. Аксиома аддитивности (частный случай аксиомы счетной аддитивности): p(A + B) = p(A) + p(B), если Aи B несовместны.

3. 
   p() = 1.
   

Аксиомы 1–3 составляют основу всей теории вероятностей. Все теоремы этой теории, включая самые сложные, выводятся из них формально-логическим путем. В частности, важнейший результат, который потребуется в дальнейшим, есть формула полной вероятности. Пусть наступление некого события А зависит от сопутствующих событий B₁, B₂, … , B_i…, которые сами наступают с вероятностями p(B_i), iI. Условной вероятностью называется вероятность p(A/B_i) события А при условии наступления события B_i. Тогда полная вероятность события А есть величина

p(A) = _iI p(B_i) p(A/B_i) (1.4.1)

Случайной величиной, связанной с данным опытом, называется величина, которая при каждом осуществлении этого опыта принимает то или иное числовое значение, заранее неизвестно, какое именно.

Любое правило, устанавливающее связь между возможными значениями случайной величины и их вероятностями, называется распределением вероятностей (или просто распределением) случайной величины.

Табличка вида

x1	x2	…	xn	…
p1	p2	…	pn	…

задает распределение случайной величины X.

Здесь x₁, x_2, …, x_n, … – возможные значения величины Х, а p₁, p₂, …, p_n, … – их вероятности. Понятно, что p_i  0 и

_i=1..np_i =1.

Последнее соотношение называют условием нормировки.

Рассмотренный способ задания распределения вероятностей применим только в том случае, когда случайная величина может принимать лишь конечное или счетное множество значений, такие случайные величины называются дискретными.

В некоторых задачах определение всех значений p_i вызывает серьезные затруднения, поэтому зачастую на практике распределение вероятностей характеризуется каким-то набором чисел, которые называются параметрами. Важнейшим параметром является математическое ожидание или среднее значение случайной величины.

Математическим ожиданием или средним значением дискретной случайной величины X, заданной распределением вероятностей

x1	x2	…	xn	…
p1	p2	…	pn	…

называется сумма

M(X) = x₁∙p₁ + x₂∙p₂ + … + x_n∙p_n + …

Таким образом, математическое ожидание дискретной случайной величины Х равно сумме произведений возможных значений величины Х на их вероятности.

Математическое ожидание есть некий центр, вокруг которого группируются возможные значения случайной величины.

Дисперсией случайной величины Х называется число, определяемое формулой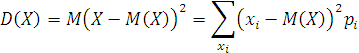



Таким образом, дисперсия есть математическое ожидание квадрата отклонения случайной величины Х от её математического ожидания. Дисперсия характеризует величину возможного разброса значений случайной величины вокруг их центра.

При изучении самых разнообразных систем и явлений действительности встречаются процессы, точно предсказать течение которых заранее невозможно. Например, нет никакой возможности заранее предсказать численный состав колонии бактерий, а также расположение каждой бактерии внутри колонии. Такие процессы называются случайными.

Математическая модель случайных процессов реального мира – это функция от времени t, значения которой – случайные величины. Договоримся такую функцию от времени также называть случайным процессом.

Случайный процесс является математической моделью для описания случайных явлений, развивающихся во времени. При этом предполагается, что состояние процесса в текущий момент времени есть некоторая случайная величина.

4.2. Понятие о марковских процессах

Вернёмся к модели динамической системы из п. 1.3.1. Во многих случаях исследователь не может точно задать вектор‑функции выхода F и перходов G, т.е. детерминировать их. Это значит что наряду с известными вектор‑переменными X, Y, Z в системе действует неопределенный фактор . В благоприятных случаях (а их большинство) этот фактор можно представить случайной величиной или вероятностью. Такие факторы, процессы, системы и задачи называются стохастическими. Наиболее просто исследовать стохастические системы, обладающие свойством марковости.

Случайный процесс называется марковским, если для любого момента времени t₀ вероятностные характеристики процесса при t > t₀зависят только от его состояния Q(t₀) и не зависят от того, каким образом было достигнуто состояние Q(t₀) при t < t₀. Иными словами, марковский процесс «не помнит» своей предыстории. Он «помнит» только текущее состояние.

4.3. Автономный вероятностный автомат

Не трудно видеть, что этим свойством, по определению, обладает дискретный автомат. Пусть мы не можем (или не хотим, или не имеет смысла) задать случайный фактор , переводящий автомат из состояния в состояние. Зато мы можем путём наблюдений узнать множество P вероятностей p_ijпереходов (q_i q_j) из i‑того состояния в j‑тоеи задать функцию

 : Q²  P

где p_ij  [0, 1] – вероятности переходов, Q – множество состояний системы.

Функцию  легко задать матрицей Q = || p_ij||, где p_ij – вероятность перехода из i‑того состояния в j‑тое: (q_i  q_j), i, j  {0, 1, 2, …, n}.

Q	q1	q2	q3	…
q1	p11	p12	p13	…
q2	p21	p22	p23	…
q3	p31	p32	p33	…
…	…	…	…	…

Σ_j = 1..n p_ij = 1 при любом i = const.

Полученная модель стохастической системы есть автономный вероятностный автомат. В отличие от ранее рассмотренных автоматов, автономный автомат не имеет входа, но зато переходит из состояния в состояние без внешнего воздействия. Такими свойствами обладают многие реальные системы.

Матрица Q называется стохастической. Имея стохастическую матрицу, мы не можем указать конкретное состояние, в которое система попадёт в следующем такте. Зато мы можем попытаться вычислить вероятность P_i пребывания стохастического автомата в i‑том состоянии, то есть долю времени, которую автомат пребывает в состоянии q_i за достаточно длительный срок.

Состояние стохастической системы недетерминировано, но можно задать распределение вероятностей состояний Р = {Р₁, Р₂,…, Р_n}. Это распределение – стохастический вектор Р, по определению, удовлетворяет условию нормировки:

∑_i = 1..n Р_i = 1 (4.1)

Вектор Р – вектор‑строка вероятностей состояний. Договоримся верхним индексом указывать момент k времени (номер такта), к которому относится данное распределение вероятностей состояний Р^(k). Исходя из формулы полной вероятности можно убедиться, что в (k+1)‑м такте вероятности Р_i в стохастическом векторе Р получаются умножением вектора на матрицу по правилам алгебры матриц. Далее  – матричное умножение.

Р^(k+1) = Р^(k) Q (4.2)

Очевидно, что все Р^(k) при k = 0, 1, 2,… тоже будут стохастическими векторами, отображающими распределение вероятностей Р_iпри различных k.

В иной форме динамику стохастического автомата можно описать, если вычислить приращение вероятности в течение одного такта.

∆Р = Р^(k+1) – Р^(k) = Р^(k)(Q – Е) = Р^(k) D (4.3)

где Е – единичная диагональная матрица, D – оператор девиации (изменения, отклонения) вектора Р за единичное время ∆t = 1. Если теперь взять за длину такта бесконечно малый интервал ∆t  0, то можно перейти к дифференциальному уравнению

dP/dt = Р  D (4.4)

4.4. Эргодичность и стационарность

Система называется эргодической, если из любого состояния она может быть переведена в любое другое за конечное число шагов. Иными словами граф переходов эргодической системы сильно связен.

Эргодические системы имеют ряд полезных свойств. В теории вероятностей показано, что в эргодических системах при k  ∞ все Р_i^(k) стремятся к финальным вероятностям: lim Р_i^(k) = Р_i фин. Соответственно, Р^(k)  Р_фин.

Ясно, что по достижении финальной вероятности Р_фин, система достигнет стационарного режима, т.е. вектор Р стабилизируется и его производная станет равна нулю. Уравнение для стационарного режима в векторной форме выглядит совсем просто.

Р_фин D = 0 (4.5)

После раскрытия произведения получается система из n однородных линейных уравнений, дополняемая уравнением нормировки (4.1), что и обеспечивает решение.

Возвращаясь к эргодичности, заметим, что в стационарном состоянии процессы в эргодических системах обратимы, т.е. не зависят от знака времени. Если снять обратимый процесс на киноленту, а потом её просматривать, то мы не сможем отличить, в какую сторону прокручивается кино – по ходу событий или в обратном направлении. Важнейшую роль эргодичность играет в классической термодинамике и статистической физике. Но вернёмся «к нашим баранам».

4.5. Пример 2. Задача о хвостистах.

П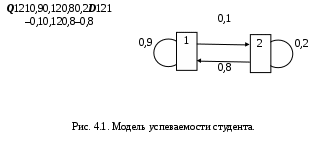
усть успехи студента в учебе описываются вероятностным автоматом с двумя состояниями: 1 – все экзамены сданы и 2 – у студента есть «хвост». За такт возьмем 1 семестр, Р⁽⁰⁾ = {0,5; 0,5}, стохастическая матрица Q, девиатор D и граф переходов показаны на Рис. 4.1.

Выполняя преобразование (4.2) по правилам алгебры матриц

Р_j = ∑_i =1..n(Р_i  p_ij)

получим следующую последовательность

Р⁽⁰⁾ = {0,5; 0,5} – сначала мы ничего не знаем об успеваемости

Р⁽¹⁾ = {0,45 + 0,40; 0,05 + 0,10} = {0,85; 0,15}

Р⁽²⁾ = {0,765 + 0,12; 0,085 + 0,03} = {0,885; 0,115}

Р⁽³⁾ = {0,8885; 0,1115}… и т.д. до Р_фин = {1 – 0,1(1); 0,(1)}≈{0,89; 011}

Итак, более 10% студентов оказались «хвостистами» и будут рано или поздно отчислены.

Найдём финальные вероятности, не прибегая к итерациям. Выпишем уравнения для вероятностей состояний:

Р_j = ∑_i =1..n Р_i  p_ij

∑_{i = 1..n} P_i = 1 (i = 1.. n)

Решение этой системы и есть вектор Р финальных вероятностей. В нашем примере

0,8 Р₂ – 0,1 Р₁ = 0

0,1 Р₁ – 0,8 Р₂ = 0

Р₁ + Р₂ =1

Р₁ = 0,8(8)

Р₂ = 0,1(1)

4.6. Метод динамики средних

Здесь мы исследовали всего один элемент системы, а вывод делаем относительно всего множества элементов. В теории вероятностей доказывается, что такой перенос свойств элемента на весь ансамбль допустим для эргодическихсистем.

Вернёмся к графу переходов вероятностного автомата или марковского процесса. Мы приписывали вес равный вероятности или интенсивности перехода каждой дуге графа и этого было достаточно для написания дифференциальных уравнений динамики вероятностей Р_iсостояний системы. Запишем в каждую вершину q_i среднее число элементов N_i = Р_i∙N, находящихся в нём. Такой граф переходов в дальнейшем называется маркированной сетью. Условие нормировки для замкнутой системы теперь примет вид

∑_{i = 1..n} N_i =  N , (i = 1.. n)

и наши уравнения будут описывать динамику средних значений величин N_i. Такой перенос результатов с одного элемента на весь ансамбль называется методом динамики средних, поскольку он основан на том факте, что отдельный элемент системы ведёт себя как все прочие элементы и как сама система в среднем. Метод тем точнее, чем больше ансамбль.

Одним из первых метод динамики средних применил Гиббс при построении статистической механики, подтвердившей все результаты классической феноменологической термодинамики статистическими методами. Поэтому стационарные состояния больших ансамблей, полученные этим методом, называют ещё и гиббсовскими состояниями. В последнее время для стационарных состояний динамических систем утвердился термин аттрактор – состояние, притягивающее к себе процесс.

5. Асинхронные марковские модели

5.1. Потоки событий

Рассмотрим теперь дискретные марковские процессы с непрерывным временем, когда моменты возможных переходов неопределенны и случайны. В этом случае мы уже не можем задать какой‑то фиксированный такт, во время которого происходит переход. Переходы нашего вероятностного автомата происходят в случайные моменты времени. Такие модели систем мы будем называть асинхронными.

Последовательность одинаковых событий, следующих одно за другим в случайные моменты времени называется потоком событий. Потоки событий – это и есть те случайные факторы , которые делают поведение системы стохастическим. Однако, в отличие от теории вероятностей, здесь термин событие не означает исход какого‑то опыта. Событие – мгновенное изменение состояния системы – не имеет вероятности. Вероятностями обладают промежутки времени между событиями, факт появления события на каком‑то интервале времени и т.п.

Таким образом, событие не имеет длительности. Точнее, длительность реального события настолько мала, что в математической модели потока событий ею можно пренебрегать.

Поток событий можно представить точками на оси времени (Рис. 5.1.).


Поток событий характеризуется двумя величинами:

1. 
   Интенсивность  – среднее число событий приходящихся на единицу времени. Интенсивность может быть как постоянной:  = const, так и функцией от времени: = (t). Величина = 1/ называется средним интервалом времени между событиями.
   
2. 
   Вероятность P_n(t) того, что в интервале времени [0, t] произойдет n событий. Таким образом, число n событий в интервале времени t есть случайная величина n = n(t). В общем случае P_n(t) зависит от времени.
   

5.2. Классификация потоков событий

1. Поток называется регулярным, если интервалы времени  между событиями равны друг другу  = const. На практике такие потоки редко встречаются и для них существуют специальные методы анализа.

2. Поток называется стационарным, если его характеристики не зависят от времени:  = const. Фактическое число события n(t) – случайная величина, но для фиксированных n и t вероятность P_n(t) = const.

Случайные сгущения и разрежения событий в потоке еще не означают, что поток нестационарен. Нарушение стационарности обычно имеет ясную физическую причину. Таковы, например, сгущения потоков клиентов в «часы пик». Причина таких сгущений – единое расписание работы всех горожан. В таких случаях модель стационарного потока имеет смысл для определенного периода времени. Так в рабочее время интенсивность потока клиентов равна _раб – до конца рабочего дня, _пик – пиковая интенсивность, _веч – вечером, _ноч – ночью. При этом _ноч < _раб ≤ _веч <_пик. Многие потоки можно считать стационарными на ограниченных участках времени. При грамотном анализе систем такие неоднородности могут быть и должны быть учтены.

3. Поток называется потоком без последействий, если для любых двух непересекающихся интервалов времени t₁ и t₂ число событий на интервале t₂ не зависит от числа событий на интервале t₁. Иными словами, события в потоке независимы друг от друга.

Например, поток покупателей, идущих в гастроном, не имеет последействия, а поток покупателей, отходящих от кассира, последействие имеет. Каждому из них нужно время для расчета с кассиром, и в это время от кассира покупатель не отходит. Впрочем, если средний интервал времени  между событиями много больше времени обслуживания у кассира, то последействием можно пренебречь и считать обслуживание точечным событием.

4. Поток событий называется ординарным, если события в нём появляются поодиночке, а не группами. С математической точки зрения это означает, что вероятность попадания двух событий в бесконечно малый интервал времени dt является величиной более высокого порядка малости, чем вероятность одного события. Так очевидно, что при интенсивности λ попасть в интервал dt событие может с вероятностью dp = λdt, а два события могут попасть туда же с вероятностью dp² = λ²dt² = (λdt) = (dp). Величина (x) называется величиной более высокого порядка малости по сравнению с x. В математическом анализе показано, что такими величинами можно пренебрегать при интегрировании без потери точности вычислений.

5.3. Простейший поток

Простейший поток событий обладает сразу тремя свойствами. Он стационарен, ординарен и без последействия. Рассмотрим простейший поток на интервале [0; t + dt]. Вычислим вероятность P_n(t + dt) того, что на этом интервале произойдёт n событий. Это возможно в двух случаях.

1. Все n событий произошли с вероятностью P_n(t) на интервале [0; t] и ни одного события не произошло на интервале [t;t + dt]. Поскольку на этом интервале длительности dt может произойти не более одного события, вероятность отсутствия события равна

P₀(dt) = 1 – λdt (5.1)

2.Предшествующие(n – 1) события с вероятностью P_n‑1(t) произошли на интервале [0; t], а одно n‑тое событие произошло на интервале [t; t + dt] с вероятностью

P₁(dt) = λdt (5.2)

Итак, имеем рекуррентное уравнение

P_n(t+ dt) = P_n(t)[1– λdt]+ P_n‑1(t)λdt (5.3)

Отсюда:

[(P_n(t + dt) – P_n(t)]/dt = dP_n(t)/dt = λ[P_n‑1(t) – P_n(t)](5.4)

Для n = 0 используя (5.1) имеем следующие выкладки

P₀(0) = 1

P₀(t + dt) = P₀(t)P₀(dt) = P₀(t)[1 – λdt]

dP₀(t)/dt = – λP₀(t) – уравнение с разделяющимися переменными.

Разделим их

dP₀(t)/P₀(t) = – λdt – уравнение экспоненты

Интегрируя левую и правую части на отрезке [0; t] имеем

∫_0..t dP₀(t)/P₀(t) = – λ ∫_0..t dt

ln[P₀(t)/P₀(0)] = – λt

P₀(t) = e ^– λt (5.5)

Итак, вероятность P₀(t) того, что в простейшем потоке событие не произойдёт на интервале [0, t] падает от 1 до 0, причём тем быстрее, чем больше интенсивность потока.

Гораздо сложнее и интереснее дело обстоит с вероятностью P_n(t). В теории вероятностей показано, что решением рекуррентного уравнения (5.3) является распределение Пуассона.

P_n(t) = (λt)ⁿ e^– λt/n!

Простейший поток событий и распределение Пуассона играют ту же роль, что случайные отклонения показаний прибора и распределение Гаусса в теории ошибок. Статистика ошибок получается, как сумма случайных отклонений произвольного характера. Простейший поток – перемешивание большого числа различных потоков событий.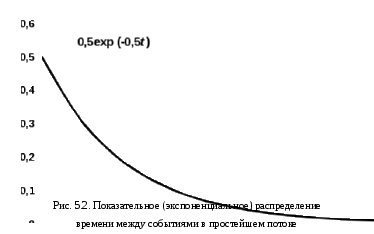


Обратим внимание на распределение времени  между событиями простейшего потока. Запишем формулу для вероятности Р(  t) того, что промежуток времени  между событиями простейшего потока будет меньше или равен t: (  t). Событие (  t) – отрицание события ( > t), а последнее состоит в отсутствии событий простейшего потока в течение времени t. Вероятность его P₀(t) нам известна из (5.5). Отсюда

Р(  t) = 1 – P₀(t) = 1 – e^– λt

Дифференцируя Р(  t)по t получим плотность распределения времени :

Р(  t) = p(t) = e^– λt

Это распределение называется показательным или экспоненциальным и показано на Рис. 5.2.

5.4. Другие потоки событий

На практике встречаются потоки событий, отличающиеся от простейшего потока. Например, кассир обслуживает покупателя некоторое случайное время , распределённое по нормальному закону.

Поток событий называется рекуррентным или потоком Пальма, если он стационарен и ординарен, а интервалы между событиями ₁, ₂, ₃,… – независимые случайные величины с одинаковым распределением, причём любым. В частности, простейший поток – это рекуррентный поток с показательным распределением времени между событиями. Регулярный поток – тоже рекуррентный, но с вырожденным распределением для . Это постоянная величина или очень «острое» нормальное распределение.

Другим способом получения потока является просеивание простейшего потока. Пусть простейший поток посетителей учреждения сортируется диспетчером по k различным направлениям, так что на каждое i‑тое направление попадает посетитель с номером j по правилу i = j(mod k).В этом случае по i‑тому направлению будет направлен так называемый поток Эрланга k‑того порядка. Интервал между событиями в потоке Эрланга – сумма интервалов из простейшего потока. В частности, простейший поток событий – это поток Эрланга 1‑го порядка. При k  ∞ поток Эрланга превращается сначала в поток Пальма с нормальным распределением для , а далее – в регулярный поток. Важно следующее утверждение.

• 
  Системы, в которых все потоки простейшие, являются марковскими.
  

5.5. Уравнения Колмогорова‑Чепмена для замкнутой системы

Вернёмся к модели стохастической системы с дискретными состояниями и непрерывным временем. Такую систему можно описать асинхронным вероятностным автоматом. В этом случае каждому переходу (q_i q_j) соответствует интенсивность λ_ij потока событий, состоящих в реализации этого перехода. Будем полагать, что этот поток простейший, и в каждый момент времени в нём выполняется только один переход. Ординарность потоков событий обеспечивает применимость простой автоматной модели. Наглядно такую систему можно изобразить графом переходов марковского процесса:

G = <Q, U, α:Λ  U>

где:

Q – множество состояний системы, |Q| = n.

U – множество переходов (q_iq_j)  U, U  Q²

Λ – множество интенсивностей переходов λ_ij, приписанных отображением α дугам (переходам) графа G.

Отображение α можно задать матрицей Λ размерами nn. В её клетках расположены интенсивности λ_ij. Как и в модели с дискретным временем нас будет интересовать стохастический вектор Р(t) = {P₁(t), P₂(t),…, P_n(t)}, где P_i(t) – вероятность нахождения системы в состоянии q_i в момент времени t, иначе говоря – доля времени, которую система проводит в этом состоянии.

Итак, возможны два типа марковских моделей стохастических систем: синхронная и асинхронная. В синхронной модели система рассматривается как множество одинаковых синхронных вероятностных автоматов, заданных стохастической матрицейQ вероятностей p_ij для переходов (q_i q_j). Поведение системы представляется одним таким автоматом на большом промежутке времени.

В асинхронной модели система рассматривается как множество одинаковых аксинсинхронных вероятностных автоматов, заданных матрицей Λ интенсивностей λ_ij, для тех же переходов (q_i q_j). Поведение системы представляется одним асинхронным автоматом на большом промежутке времени.

Процесс в обеих этих моделях имеет две проекции: история – последовательность состояний и тайминг – последовательность переходов. В синхронной модели на первом месте стоит история системы – последовательность состояний, изменяемых одновременно во всех элементах системы в каждом такте. В асинхронной модели тактов нет, а процесс функционирования системы лучше представляется таймингом – ординарным потоком событий‑переходов q_i q_j из состояния q_i в состояниеq_j, происходящих в случайные моменты времени.

Каково соотношение между этими моделями? Интуитивно ясно, что если эти две модели описывают одну и ту же систему, то и результаты моделирования должны совпадать, т.е. эти модели в каком-то смсысле эквивалентны. Действительно.

Рассмотрим матрицы D и , описывающие динамику синхронной и асинхронной модели, соответственно. Эти матрицы таковы, что вероятности p_ij перехода q_i q_j в матрице D соответствует интенсивность _ij потока переходовq_i q_j в матрице . Более того, сумма элеменов каждой строки в обеих матрицах по определению равна 0. (Напомним, что D= Q– E, а в матрице Qсумма элементов строки равна 1). Пусть P_ij(t) – вероятность перехода q_i q_j за время t. Ранее было показано, что вероятность одного этого перехода за время   t  равна

Р_ij(t) = 1 – P₀(t)= 1 – e^– λt

а плотность распределения для Р_ij(t) – это вероятность p_ij перехода q_i q_j в данный момент времени (т.е. за время одного такта   dt)

p_ij= P_ij(dt) = P₁(dt) = λdt

Здесь мы взяли dt за длительность такта. Итак, доказан следующий

Принцип эквивалентности синхронные и асинхронные марковские модели эквивалентны и D = k. Подбирая коэффициент k можно сделать D матрицей вероятностей, а – матрицей интенсивностей. Изменяя единицу времени (дительность такта) можно переводить матрицы D и  друг в друга.

Рассмотрим внимательнее матрицу Λ. Если i ≠ j, то в клетке матрицы Λ стоит λ_ij – интенсивность перехода q_i → q_j. Если же i = j, то в клетке λ_ii должна стоять интенсивность потока выходов из состояния q_i, причём с отрицательным знаком.

λ_ii = – Σ _j  i λ_ij

и тогда

Σ_j=1..n λ_ij = 0

Это значит, что никуда из множества состояний Q система не выходит.

Пусть теперь P – вектор‑строка вероятностей состояний, P' = dP/dt – вектор‑строка производных от вероятностей состояний.

Тогда по правилам алгебры матриц

P' = P  Λ (5.6)

Σ_i=1..nP_i(t) = 1

Эти система уравнений носит имя уравнения Колмогорова‑Чепмена. Для ее решения необходимо задать начальное условие, т.е. значение вектора P в момент t = 0. Обычно это вектор вида P = <1, 0, 0, …, 0>, где q₁ – начальное состояние, P₁(0) = 1.

Спрашивается, что будет происходить с вероятностями состояний P_i(t) при t → ∞ ? В теории случайных процессов доказывается, что если число n состояний системы конечно, и из любого i‑того состояния можно попасть в любое j‑тое за конечное число шагов, то вероятности P_i= lim P_i(t) при t   существуют и называются финальными вероятностями состояний.

Ранее мы назвали такие системы эргодическими. Финальную вероятность P_iможно трактовать, как долю времени пребывания системы в i‑том состоянии. С другой стороны эргодические системы таковы, что вместо одной системы, наблюдаемой в течение долгого времени при t → ∞ мы можем наблюдать N → ∞ идентичных систем одновременно. Тогда финальная вероятность оказывается долей систем, находящихся в i‑том состоянии.

Поскольку финальные вероятности постоянны, то говорят, что система достигла стационарного состояния. При этом все производные P'_i = 0 и система уравнений Колмогорова‑Чепмена становится системой линейных однородных уравнений с одним условием нормировки.

P  Λ = 0 (5.7)

Σ_i=1..nP_i(t) = 1

Такая система легко решается методом исключения неизвестных. При этом можно не рассматривать одно из однородных уравнений.

5.7. Пример 3. Ненадёжный агрегат

Пусть некий агрегат имеет 3 состояния:

q₁– агрегат исправен и дает прибыль S₁в единицу времени.

q₂ – агрегат неисправен, и диагностируется, что требует расходов S₂ в единицу времени.

q₃– агрегат ремонтируется, что обходится в сумму S₃в единицу времени.

Таким образом, математическое ожидание прибыли составляет

S = P₁ S₁ – P₂ S₂ ­– P₃ S₃

где: P_i– вероятность состояния q_i, т.е. доля рабочего времени, которую агрегат проводит в состоянии q_i.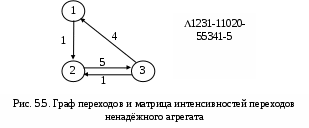

Предшествующий опыт эксплуатации показал, что агрегат переходит из состояния в соответствии с графом переходов, показанным на Рис. 5.4. Переход (3  2) происходит при ошибочной диагностике. За единицу времени можно взять и 1 сутки, и 1 месяц, и 1 год. Здесь это всё равно, главное, чтобы все интенсивности измерялись в одинаковых единицах. Спрашивается, при каких значениях S₁, S₂ и S₃ агрегат приносит прибыль? Очевидно, таковым условием является S > 0 или P₁S₁– (P₂S₂  + P₃S₃) > 0.

Найдем P₁, P₂ и P₃ в стационарном режиме. Построим, прежде всего, матрицу интенсивностей переходов  и воспользуемся матричной формулировкой уравнений Колмогорова‑Чепмена.

При составлении этих уравнений вручную можно пользоваться следующим правилом. Производная P'_i равна разности суммарного входного и суммарного выходного потоков. В стационарном режиме эта разность равна нулю, т.е. входной и выходной потоки в каждом состоянии равны. Просматривая состояние за состоянием на Рис. 5.4. имеем систему уравнений:

для q₁: P₁ = 4P₃

для q₂: P₁ + P₃ = 5P₂

для q₃: 5P₃ = 5P₂

Нормировка: P₁ + P₂ + P₃ = 1

Нетрудно убедиться, что этот простой метод даёт тот же результат, что и умножение вектор‑строки P на матрицу . Решая систему уравнений получаем:

P₁ = 2/3; P₂ = 1/6; P₃ = 1/6

Пусть S₁ = 300; S₂ = 200; S₃ = 400

S =2/3(300) – 1/6(200 + 400) = 200 – 100 = 100

Эксплуатация агрегата даёт прибыль.

Задачи к главе 2

Задачи к главе 2 предназначены для решения на практических занятиях. Они легко решаются аналитически и вручную для стационарного режима. Для более глубокого освоения теории желательно решить их для переходного режима. Впрочем, это можно отложить до освоения главы 3 и работы в компьютерном классе. Тогда можно будет исследовать и переходной, и стационарный режимы с помощью программы «Популяция».

Как показывает опыт, наибольшие затруднения при решении сюжетных задач вызывает переход от словесной формулировки задачи к математической модели. При этом особенно трудно осваивается задание системы интенсивностей переходов в единой системе единиц измерения времени для каждого перехода. В сюжетной задаче эти интенсивности задаются по‑разному. Рекомендуется следующий порядок действий.

1. 
   Нарисовать граф переходов. Для этого необходимо сначала выписать все необходимые состояния системы, а затем соединить их дугами.
   
2. 
   Выбирается длительность такта и все интенсивности переходов (или их вероятности) относятся к этому такту. Лучше делать это с интенсивностями. Дуги графа переходов подписываются полученными числами.
   
3. 
   Если в задаче есть интенсивности и вероятности, следует пересчитать всё в интенсивностях.
   
4. 
   Если некоторые интенсивности получились больше 1, то следует уменьшить длительность такта и, соответственно, все интенсивности (вероятности) поделить на такую величину (обычно степень десяти), чтобы все числа стали меньше 1, а сумма вероятностей выходов из любого состояния была не больше 1.
   
5. 
   Составить матрицы переходов Q и Dили матрицу интенсивностей .
   

Используя граф переходов и матрицы Dи записать систему линейных уравнений и уравнение нормировки для вероятностей состояний. В случае с интенсивностями это будут уравнения Колмогорова‑Чепмена.

6. 
   Решить систему.
   

При использовании программы «Популяция» решение системы получается автоматически и в переходном режиме (см. Гл. 3). Задачи даны в порядке увеличения сложности.

1. Задача о пьяницах

Для рытья канавы наняли 100 пьяниц. После работы пьяница напивается с вероятностью 0,5. На следующий день по пути на работу напившийся вчера пьяница опохмеляется и с вероятностью 0,5 снова напивается и не доходит до рабочего места. Сколько пьяниц действительно копают канаву?

2. Задача о враче

Рабочий день врача 8 часов, т.е. 480 минут. На осмотр больного уходит в среднем 15 минут. После осмотра врач занимается документацией или отдыхает в среднем 2 минуты. Около 5‑ти раз в день врач отвлекается в среднем на 10 минут. Осмотр больного не прерывается. Сколько больных врач может осмотреть за один рабочий день при таком режиме работы?

3. Задача о кассирах

Кассовый аппарат требует осмотра или заправки ленты в среднем 5 минут каждые 2 часа. Кассир отвлекается от работы в среднем на 10 минут и в среднем через 1 час. На обслуживание клиента тратится в среднем 2 минуты. Рабочий день – 12 часов. Все потоки простейшие. Сколько клиентов может рассчитать кассир за рабочий день?

4. Задача о ремонте автобуса

Автобус требует профилактического осмотра в среднем 3 раза в год. Осмотр длится около 1 дня. После этого автобус готов к эксплуатации с вероятностью 0,9, а в остальных случаях его задерживают в мастерской для ремонта в среднем на 5 дней. Осмотр и ремонт обходится в 10000 рублей в день. Прибыль от эксплуатации 1000 рублей в день.

Выгодно ли эксплуатировать такие автобусы, если число дней в году 365?

5. Задача о КЭШе

Если процессор не ищет данные в памяти, то он считает, а вероятность состояния счёта – это КПД компьютера. Процессор в 10 раз быстрее основной памяти. Для ускорения доступа к данным в компьютере предлагается ввести небольшую скрытую память – КЭШ (тайник). Доступ в КЭШ в 10 раз быстрее, чем в основную память. Вероятность найти нужные данные в КЭШ равна 0,9. Если же их там нет, КЭШ обращается в основную память и пополняется, а данные одновременно попадают в процессор.

1. 
   Каков КПД компьютера без КЭШ?
   
2. 
   Как изменится КПД при введении КЭШ?