Метод k-моделирования. МЕТОД К-моделирования. 3. каузальное моделирование популяций

• Название: 3. каузальное моделирование популяций
• Анкор: Метод k-моделирования
• Дата: 25.04.2022
• Размер: 2.74 Mb.
• Имя файла: МЕТОД К-моделирования.doc
• Тип: Документы; #496372
• страница: 2 из 12

ГЛАВА 3. ДИНАМИЧЕСКИЕ МОДЕЛИ СИСТЕМ

3.1. Динамическая модель общего вида

Ниже будут изучаться системы, для которых значения переменных функциональной модели зависят от времени. Такая ситуация характерна для большинства систем. Соответственно эти системы называются динамическими, а их функциональные модели – динамическими моделями систем.

Динамическая модель может быть представлена семёркой объектов:

S_д= <X, Y, Z, F, G, T, Z₀>

где:

X – множество (вектор) входных переменных, x_i  X – компонента вектора X;

Y – множество (вектор) выходных переменных, y_i  Y – компонента Y;

Z – множество (вектор) внутренних переменных – состояний, где z_i Z;

F– вектор‑функция выхода, f_i F – компонента вектор‑функции выхода, где

y_i(t) = f_i[X(t), Z(t)];

G – вектор‑функция переходов, g_i G – компонента вектор‑функции переходов, где

z_i(t)=g_i[Z(0), X(τ)], τ  [0, t]

X(τ) – траектория входа за период времени τ – последовательность значений, принимаемых вектором X на множестве моментов системного времени в сегменте τ [0, t].

Z₀= {z₁(0), z₂(0), …, z_n(0)} – начальное состояние системы в момент t = 0.

Если во всё время функционирования Z = Z₀, тосистема «не помнит» своей истории. Выход такой системы зависит только от входа в данный момент. Такую систему уместно назвать комбинационной. Внутреннее состояние комбинационной системы можно не рассматривать.

Другой важнейший элемент системы – модель системного времени Т. Она может представлять собой натуральный ряд Т = 0, 1, 2, … или континуум Т  R, где R – множество действительных чисел. В первом случае мы имеем модель дискретного времени, во втором случае – модель непрерывного времени. Во многих случаях дискретно не только время, но и значения входных и выходных переменных. Такие системы называются дискретными.

Наконец, следует различать замкнутые и открытые системы. В замкнутой системе все элементы постоянно присутствуют, а их общее количество не изменяется. Число состояний замкнутой системы равно произведению чисел состояний всех её элементов. Например, n‑разрядный двоичный регистр, хранящий число в памяти компьютера, можно рассматривать как систему, состоящую из n элементов, каждый из которых имеет два состояния 0 и 1. Число состояний такой системы, как известно, равно 2ⁿ. Замкнутую систему значительно легче исследовать в силу неизменности её мощности.

В открытой системе число элементов изменяется в процессе её функционирования. Они появляются в системе извне и уходят из системы во внешнюю среду. Такими свойствами обладают, например, популяции живых организмов, системы обслуживания потока клиентов и т.д. и т.п. При моделировании открытой системы принципиально невозможно перечислить все её элементы, однако в самой системе в каждый момент времени находится определённое их число. Для моделирования внешней среды можно ввести специальный внешний элемент, который используется как источник входного потока новых элементов и поглотитель выходного потока отработавших.

3.2. Дискретный конечный автомат

Дискретный автомат – модель замкнутой системы с дискретными переменными и дискретным временем. Широко распространена модель конечного дискретного автомата, где время: T = 0, 1, 2, 3, … дискретно по умолчанию и не рассматривается в явной записи. Дискретный автомат Мили можно задать шестёркой математических объектов:

Autom= <A, B, Q, f, g, q₀>

A, B, Q – конечные алфавиты (наборы символов, букв) входа, выхода и внутренних состояний, соответствено;

f – функция выхода вида b(t) = f(q(t), a(t))

g – функция переходов вида q(t+1) = g(q(t), a(t))

q₀ – исходное состояние в момент времени t = 0.

Здесь a(t), b(t), q(t)– буквы из алфавитов A, B, Q, соответственно, в момент t T.

Обратим внимание на конечность всех алфавитов дискретного автомата. Эта модель используется, следовательно, для исследования конечных систем. В теории вычислений показано, что конечный автомат не может реализовать многие вычислительные процессы, заданные алгоритмами. Если допустить бесконечный алфавит состояний, то получится система, способная реализовать любой вычислительный процесс. Такова, например, абстрактная машина Тьюринга, имеющая бесконечную ленту памяти.

Наглядно дискретный автомат можно представить графом функционирования

G(Q, V, α : A V, β : B V)

Где:

Q – множество вершин, соответствующих состояниям автомата.

V – множество дуг, соответствующих переходам автомата согласно функции g.

α и β – помечают дуги соответствующими символами входа и выхода.

Более подходящим представлением для анализа автомата является матричное представление, состоящее из двух матриц.

Матрица переходов G: A× Q Q

Матрица выходов F: A× Q B

Строки матриц G и F соответствуют входному алфавиту, столбцы соответствуют алфавиту состояний. На пересечении строк и столбцов в матрице G будут находиться символы из алфавита состояний, а в матрице F – символы алфавита выходов.

В позиции G_ij записано новое состояние

g_ij = g(q_j, a_i)

В позиции F_ijзаписывается выход автомата

f_ij = f(q_j, a_i).

3.3. Пример 1. Накапливающий сумматор по модулю 4.

Накапливающий сумматор складывает входное число с тем, что было накоплено во время предыдущего функционирования. Результирующую сумму по mod4 сумматор выдает на выходе и запоминает в своем состоянии. В этом случае все три алфавита совпадают.

А = B = Q = {0, 1, 2, 3}

Матрицы переходов и выходов показаны в Табл. 3.1.

Таблица 3.1.
Матрицы переходов и выходов сумматора по mod 4.
G =	G	Q	0	1	2	3	F =	F	Q	0	1	2	3
		0	0	1	2	3		A	0	0	1	2	3
	A	1	1	2	3	0			1	1	2	3	0
		2	2	3	0	1			2	2	3	0	1
		3	3	0	1	2			3	3	0	1	2

Нетрудно видеть, что в нашем случае выход совпадает с состоянием, т.е. матрица F является излишней.

Вообще, если выход зависит только от состояния автомата, то такая модель называется автоматом Мура. Функции переходов и выходов для автомата Мура имеют вид:

q(t+1) = g[q(t), a(t)]

b(t) = f [q(t)]

Очевидно, что

b(t)=f [g [q(t – 1), a(t – 1)]] = f*[q(t – 1), a(t – 1)],

где f* – суперпозиция функций f и g.

Мы видим, что выход автомата Мура сдвинут на один такт, т.е. отстаёт от выхода автомата Мили на 1 такт, поэтому автомат Мура иногда называется сдвинутым.

Граф функционирования нашего сумматора показан на Рис. 3.1.

В Таблице 3.2. показано функционирование нашего автомата из начального состояния 0 при входной последовательности 1, 3, 0, 2, 4, 2, 3, 3, …

В моделях Мили и Мура не конкретизировано, каким образом происходит отсчёт времени. По способу отсчёта времени дискретные системы делятся на два класса синхронные и асинхронные. В синхронных системах есть специальные часы – тактовый генератор, который выдает последовательность тактовых импульсов стационарной частоты.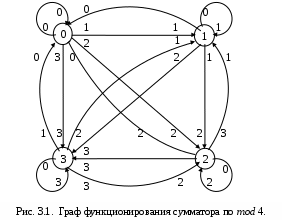

Таблица 3.2.
Функционирование сумматора по mod 4
Такт	1	2	3	4	5	6	7	8	9
Вход	1	3	0	2	1	2	3	3
Состояние	0	1	0	0	2	3	1	0	3
Выход Мили	1	0	0	2	3	1	0	3
Выход Мура	0	1	0	0	2	3	1	0	3

В асинхронных системах тактового генератора нет, и такты отсчитываются по событиям на входе в систему. Таким образом, длительность такта в асинхронных системах произвольна. Можно считать асинхронный автомат моделью системы с дискретными состояниями и непрерывным временем.

3.4. Линейные модели систем

В непрерывных случаях рассматриваются линейные и нелинейные системы. Для линейных моделей выполняется принцип суперпозиции:

[x(t) = x₁(t) + x₂(t)]  [y(t) = y₁(t) + y₂(t)]

где: x(t), x₁(t), x₂(t) Х; y(t), y₁(t), y₂(t) Y

Для этого необходимо, чтобы множества значений X, Yи Z представляли собой линейные пространства, а вектор‑функции F и G были бы линейными операторами. Если эти пространства имеют топологическую структуру, то на них можно строго определить основные понятия математического анализа (непрерывность, сходимость и.т.д., и т.п.) и задавать метрику – меру близости между элементами. Если, наконец, линейные операторы F и G непрерывны в этой топологии, то такие системы называются гладкими. Для гладких систем переходное отображение G является решением системы дифференциальных уравнений вида, заданной в векторном виде

dZ / dt = G (X, Z, t)

Большинство уравнений математической физики (механики и электродинамики) являются моделями гладких линейных систем. Далее мы покажем, как строить гладкие линейные модели и нелинейные модели для системного анализа в экономике, биологии, истории и социологии. Но прежде следует обсудить один методологический принцип математического моделирования.

3.5. Математические модели систем и их реализация

Реальные системы подчиняются следующему принципу причинности.

Отклик системы на внешнее воздействие не может начаться раньше этого воздействия.

Это условие часто не выполняется для математических моделей систем. При этом такие модели не обязательно «плохие» и бесполезные. В связи с этим одна из проблем теории систем – выяснение условий физической реализуемости теоретических моделей, то есть конкретных ограничений, которые должны быть наложены на модель или на реализацию для соблюдения принципа причинности.

Вообще, поскольку математические модели абстрагируются от многих свойств реальных систем, физическая реализация систем, то есть задачи синтеза и конструирования сильно усложняются. Простые математические модели функционирования приходится усложнять, а в задачу синтеза вводить дополнительные ограничения, чтобы добиться достаточной адекватности модели и реализации.

Например, в качестве математической модели логических схем долгое время использовались булевы функции. Переключение значения булевой функции с 0 на 1 и обратно считалось мгновенным и в модели не отражалось. Однако с ростом быстродействия оказалось, что временем переключения пренебрегать нельзя и пришлось ввести в модель 3‑е состояние. Так родилась 3‑значная логика, учитывающая время переключения логического элемента. С переходом на интегральные схемы оказалось, что их переключатели могут иметь ещё и состояние резистора (сопротивления). Для адекватного описания поведения таких микроэлементов потребовалась 7‑значная логика.