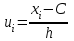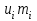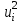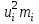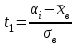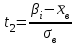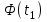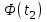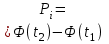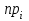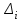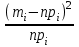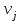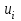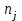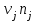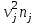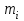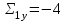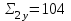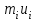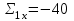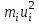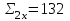А. П. Господариков, И. А. Лебедев
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
|
Пример 15. При проведении испытаний материала на разрыв получено 50 значений, характеризующих прочность на разрыв. По этим данным составлен сгруппированный вариационный ряд (масштаб 104 Па).
Оценить согласие полученных данных с нормальным распределением при уровне значимости 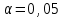 и получить приближенную интервальную оценку для параметра и получить приближенную интервальную оценку для параметра 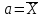 с надежностью с надежностью 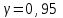 . .Решение. Введем условную варианту, определив шаг h = 20 и выбрав ложный нуль C = 190, и найдем 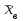 и и 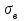 (табл.2). (табл.2).Таблица 2
По данным табл.2 имеем n = 50 и 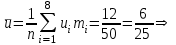 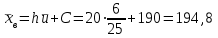 ; ;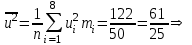 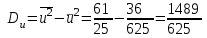 ; ;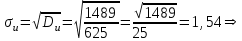 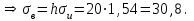 Найдем теоретические частоты (табл.3) для интервалов 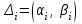 , используя формулу вероятности попадания значений в этот интервал (для нормального распределения с параметрами , используя формулу вероятности попадания значений в этот интервал (для нормального распределения с параметрами 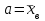 и и 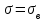 ): ):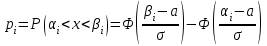 . .Таблица 3
Найдем выборочное значение 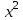 , объединив крайние интервалы для маленьких частот mi (табл.4). Это объединение не является необходимым, но вполне применимо для упрощения в случае маленьких частот. , объединив крайние интервалы для маленьких частот mi (табл.4). Это объединение не является необходимым, но вполне применимо для упрощения в случае маленьких частот.Таблица 4
Таким образом, если после объединения число интервалов 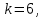 а число наложенных связей а число наложенных связей 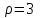 , то число степеней свободы , то число степеней свободы 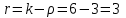 . Поэтому по таблице критических значений . Поэтому по таблице критических значений 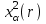 (прил.3) имеем (прил.3) имеем 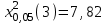 . Сравнивая найденное значение . Сравнивая найденное значение 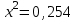 с критическим (0,254 < 7,82), получим, что рассматриваемые данные могут быть из нормально распределенной совокупности. с критическим (0,254 < 7,82), получим, что рассматриваемые данные могут быть из нормально распределенной совокупности.Для получения интервальной оценки найдем 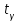 из условия из условия 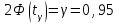 , т.е. , т.е. 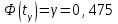 и и 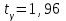 , и радиус интервала , и радиус интервала 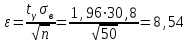 . .Вычислим доверительный интервал для параметра 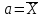 с надежностью с надежностью 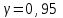 : :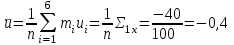 . .Пусть для изучаемой системы случайных величин (X, Y) получена выборка значений системы (xi, yi) с соответствующими совместными частотами mij 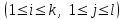 . Объем выборки . Объем выборки 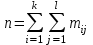 , каждое значение xi встречается с частотой , каждое значение xi встречается с частотой 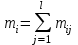 , а каждое значение yj встречается, соответственно, с частотой , а каждое значение yj встречается, соответственно, с частотой 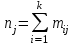 . Условные средние . Условные средние 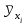 и и 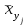 представляют отдельные значения для регрессий соответственно Y на X и X на Y: представляют отдельные значения для регрессий соответственно Y на X и X на Y: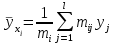 , , 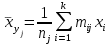 ( (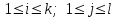 ). ).По выборке системы СВ определяют выборочные наилучшие линейные регрессии, которые приближенно выражают регрессионную (или корреляционную) зависимость между рассматриваемыми в системе случайными величинами: 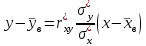 , , 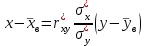 , ,где 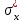 , , 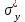 – выборочные отклонения для X и Yсоответственно. выборочный коэффициент корреляции – выборочные отклонения для X и Yсоответственно. выборочный коэффициент корреляции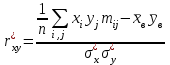 . .выборочные регрессии Y на X и X на Y приближают точки ( 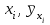 ) и ( ) и (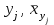 ) соответствующих условных средних ) соответствующих условных средних 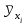 и и 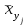 соответственно. По величине коэффициента соответственно. По величине коэффициента 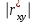 или по значению угла между прямыми выборочных регрессий можно сделать вывод о качестве связи между случайными величинами. Для расчета или по значению угла между прямыми выборочных регрессий можно сделать вывод о качестве связи между случайными величинами. Для расчета 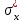 , , 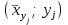 и и 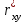 удобно использовать условные варианты для X и Y: удобно использовать условные варианты для X и Y: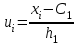 , , 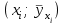 , , 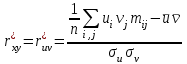 . .Пример 16. Пусть имеется 100 сгруппированных наблюдений двух измеримых признаков X и Y, по которым составлена корреляционная таблица ( 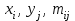 ) (табл.5). ) (табл.5).Таблица 5
Найти выборочные регрессии и оценить качество связи признаков. Решение. В табл.5 уже найдены отдельные частоты nj для yj (суммы частот mij по строкам), частоты mi для xi (сумма частот mij по столбцам) и условные средние. Например: 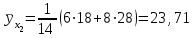 , , 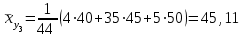 . .Соответствующие точки условных средних есть точки 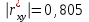 и и 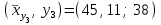 . .Для определения выборочных регрессий перейдем к условным вариантам. Наибольшая частота, ближайшая к центру таблицы, 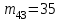 и, следовательно, соответствующие ложные нули и, следовательно, соответствующие ложные нули 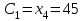 и и 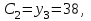 шаг шаг 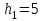 (для xi) и (для xi) и 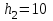 (для yj). (для yj).Составим новую таблицу в условных вариантах для расчета характеристик (табл.6). Таблица 6
По данным табл.6 получим выборочные характеристики: 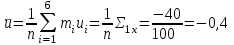 ; ;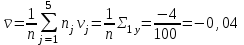 ; ;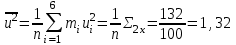 ; ;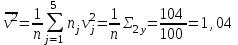 ; ;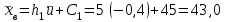 ; ;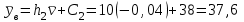 ; ;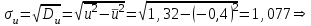 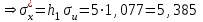 ; ;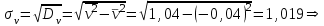 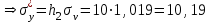 . .Для вычисления 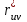 найдем средние суммы всех произведений uivjmij: найдем средние суммы всех произведений uivjmij: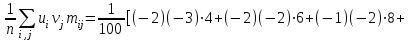 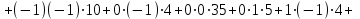 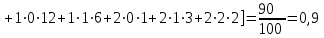 . .Выборочный коэффициент корреляции 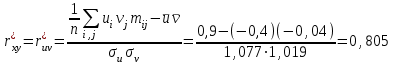 . .Уравнения выборочных регрессий имеют вид для регрессии Y на X 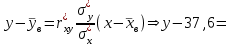 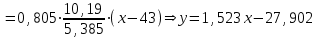 ; ;для регрессии X на Y 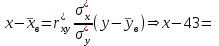 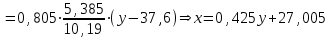 . .Обе прямых регрессий проходят через точку средних 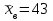 ; ; 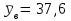 и для построения последних достаточно найти еще по одной точке для каждой прямой. и для построения последних достаточно найти еще по одной точке для каждой прямой.Так как 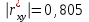 значительно отличаются от нуля, то связь между изучаемыми случайными величинами достаточно сильная, а так как это значение еще не близко к единице, связь нелинейная. Аналогичные выводы можно сделать и по величине угла между прямыми регрессий. значительно отличаются от нуля, то связь между изучаемыми случайными величинами достаточно сильная, а так как это значение еще не близко к единице, связь нелинейная. Аналогичные выводы можно сделать и по величине угла между прямыми регрессий.Для наглядности все точки условных средних 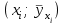 и и 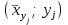 следует нарисовать на одном чертеже вместе с прямыми регрессий, причем масштаб на осях координат должен быть одинаков (чтобы избежать искажений). следует нарисовать на одном чертеже вместе с прямыми регрессий, причем масштаб на осях координат должен быть одинаков (чтобы избежать искажений). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||