А. П. Господариков, И. А. Лебедев

• Название: А. П. Господариков, И. А. Лебедев
• Дата: 20.10.2022
• Размер: 0.88 Mb.
• Имя файла: 3_ekonom__bakal (1).docx
• Тип: Учебное пособие; #745420
• страница: 8 из 12

КОНТРОЛЬНАЯ РАБОТА 6

Задача1. В ящике имеются a белых и b черных шаров. Найти вероятность того, что:

а) первый вынутый из ящика шар будет белым;

б) все вынутые из ящика kшары будут черными.

Значения a,b и k по вариантам следующие:

Вариант	1	2	3	4	5	6	7	8	9	10
a	6	3	5	10	4	6	3	5	8	7
b	5	7	8	5	66	8	7	10	4	5
k	3	4	2	3	4	5	3	4	3	3

Задача 2.

Вариант 1. В ящике имеются 5 деталей, изготовленных на станке № 1, и 10 деталей, изготовленных на станке № 2. Сборщик последовательно вынимает из ящика детали одну за другой. Найти вероятность того, что во второй раз будет извлечена деталь, изготовленная на станке № 1.

Вариант 2. Из трех орудий одновременно произведен залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,9, для второго и третьего орудия эти вероятности соответственно равны 0,8 и 0,7.

Найти вероятность того, что:

а) только одно орудие попало в цель;

б) только два орудия попали в цель;

в) все три орудия попали в цель.

Вариант 3. Три автомата производят детали, поступающие на общий склад. Производительности первого, второго и третьего автоматов относятся как 2 : 3 : 5. Вероятность того, что деталь, изготовленная первым автоматом, отличного качества, равна 0,9, для второго и третьего автоматов эти вероятности соответственно равны 0,8 и 0,85. Найти вероятность того, что наудачу взятая на складе деталь отличного качества.

Вариант 4. Для сигнализации об аварии установлены три независимо работающих устройства. Вероятность того, что при аварии первое устройство сработает, равна 0,8; для второго и третьего устройств эти вероятности равны 0,9 и 0,8 соответственно. Найти вероятность того, что при аварии сработают:

а) только одно устройство;

б) только два устройства;

в) все три устройства.

Вариант 5. В каждом из двух ящиков содержатся 3 черных и 7 белых шаров. Из второго ящика наудачу извлечен шар и переложен в первый ящик, после чего из первого ящика наудачу извлечен один шар. Найти вероятность того, что шар, извлеченный из первого ящика, окажется белым.

Вариант 6. Студент знает 45 из 60 вопросов программы. Каждый экзаменационный билет содержит три вопроса. Найти вероятность того, что студент знает:

а) все три вопроса;

б) только два вопроса;

в) только один вопрос экзаменационного билета.

Вариант 7. На трех станках при одинаковых и независимых условиях изготавливаются детали одинакового наименования. На первом станке изготавливают 10 %, на втором – 30 %, на третьем – 60 % всех деталей. Вероятность каждой детали быть небракованной равна 0,7, если изготовлена на первом станке; 0,8, если на втором станке и 0,9, если на третьем станке. Найти вероятность того, что наудачу взятая деталь окажется небракованной.

Вариант 8. Из 18 стрелков пять попадают в мишень с вероятностью 0,8, семь – с вероятностью 0,7, четверо – с вероятностью 0,6 и двое – с вероятностью 0,9. Наудачу выбранный стрелок сделал выстрел, но в мишень не попал. К какой из групп вероятнее всего принадлежал этот стрелок

Вариант 9. Имеются 10 одинаковых ящиков. В семи из них находится по четыре черных и пять белых шаров, а в трех – по три черных и шесть белых шаров. Из ящика, взятого наудачу, извлечен белый шар. Какова вероятность того, что шар извлечен из ящика, содержащего шесть белых шаров

Вариант 10. С первого станка-автомата на сборку поступает 40 %, со второго – 30 %, с третьего – 20 %, с четвертого – 10 % деталей. Среди деталей первого автомата 0,1 %, второго – 0,2 %, третьего – 0,25 %, четвертого – 0,3 % бракованных деталей. Найти вероятность того, что оказавшаяся бракованной деталь изготовлена на первом автомате.

Задача 3. При установившемся технологическом процессе вероятность изготовления детали, удовлетворяющей требованиям стандарта, равна p. Найти вероятность того, что среди взятых наудачу n деталей требованиям стандарта удовлетворяют:

а) ровно k деталей; б) хотя бы одна деталь.

Значения р, п, k, l по вариантам следующие:

Вариант	1	2	3	4	5	6	7	8	9	10
p	0,9	0,85	0,8	0,75	0,7	0,8	0,65	0,9	0,7	0,9
n	6	7	4	5	6	6	5	4	7	6
k	3	4	2	3	4	3	2	2	3	3
l	40	30	30	20	30	40	30	40	40	40

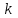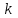Какова вероятность того, что среди 10 п деталей удовлетворяют требованиям стандарта ровно 10 деталей и от lдо 10 деталей?

Задача4.Случайная величина X задана интегральной функцией распределения: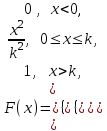



где k – номер варианта студента; α = 0,2k, β = 0,8k.

Найти дифференциальную функцию (плотность вероятности), математическое ожидание и дисперсию X, а также вероятность того, что X примет значение, заключенное в интервале (α, β). Построить графики интегральной и дифференциальной функций.

Задача5.По заданному математическому ожиданию a и среднему квадратичному отклонению σ нормально распределенной случайной величины X найти вероятность того, что X примет значение, принадлежащее интервалу α, β. Значения a,σ, α, βпо вариантам следующие:

Вариант	1	2	3	4	5	6	7	8	9	10
а	0,9	0,85	0,8	0,75	0,7	0,8	0,65	0,9	0,7	0,9
	6	7	4	5	6	6	5	4	7	6
	3	4	2	3	4	3	2	2	3	3
	40	30	30	20	30	40	30	40	40	40