А. П. Господариков, И. А. Лебедев
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
1.4. Система двух случайных величин и регрессияСистема двух случайных величин – совокупность двух случайных величин (X,Y), которые рассматриваются одновременно. Измерения обычно осуществляются попарно, а полученные значения случайных величин X и Y в определенном смысле взаимосвязаны. Закон распределения двумерной случайной величины дискретного типа представляет собой перечень значений этой величины и их вероятностей, указанных в специальной таблице. В табл.1 представлены возможные значения (xi,yj) и их совместные вероятности: 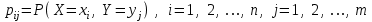 . .Таблица 1 Закон распределения двумерной случайной величины
Зная закон распределения дискретной двумерной случайной величины (X, Y), можно найти закон распределения каждой случайной величины X и Y: 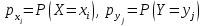 ; ;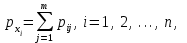 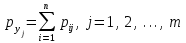 . .Интегральная функция распределения двумерной случайной величины (X, Y) есть вероятность совместного выполнения неравенств X < x и Y < y, т.е. 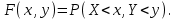 Двумерная случайная величина непрерывного типа может быть задана интегральной или дифференциальной функцией распределения. Если интегральная функция распределения всюду непрерывна и имеет непрерывную смешанную частную производную второго порядка, то дифференциальная функция распределения системы двух случайных величин (X, Y) определяется по формуле 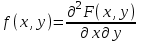 . .Плотность распределения отдельных случайных величин, входящих в систему, выражается через плотность системы случайных величин следующим образом: 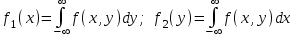 . .Условный закон распределения случайной величины, входящей в систему, есть закон ее распределения, полученный в предположении, что другая случайная величина приняла определенное значение. Для системы случайных величин дискретного типа условные законы распределения имеют вид 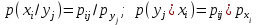 . .Условные математические ожидания (условные средние) дискретных случайных величин 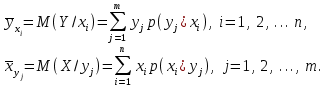 Условные распределения показывают, что одна СВ реагирует на изменение другой изменением своего закона распределения. Такая общая зависимость называется стохастической (вероятностной) и достаточно сложна для изучения. Однако зависимость условного среднего одной СВ от значений другой является функцией, которая называется регрессией: 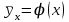 – регрессия Y на X, – регрессия Y на X, 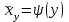 – регрессия X на Y. Но и функции регрессии в общем случае достаточно сложны, поэтому используют различные их приближения, например линейной функцией (наилучшей в смысле наименьшего значения среднего квадрата отклонения). Это значит, что для регрессии Y на X функция – регрессия X на Y. Но и функции регрессии в общем случае достаточно сложны, поэтому используют различные их приближения, например линейной функцией (наилучшей в смысле наименьшего значения среднего квадрата отклонения). Это значит, что для регрессии Y на X функция 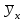 приближается линейной функцией приближается линейной функцией 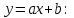 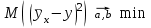 . .Уравнения таких наилучших линейных регрессий для регрессии Y на X 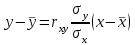 ; ; для регрессии X на Y 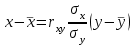 , , где 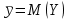 , , 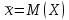 , , 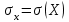 , , 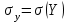 . . Коэффициент корреляции 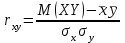 характеризует близость (или тесноту) связи между случайными величинами к линейной. Отметим, что всегда 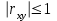 . Если . Если 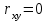 , то СВ называются некоррелированными и в этом случае их условные средние значения являются постоянными, т.е. не зависят от значений другой СВ, что характеризует их слабую взаимозависимость. Если , то СВ называются некоррелированными и в этом случае их условные средние значения являются постоянными, т.е. не зависят от значений другой СВ, что характеризует их слабую взаимозависимость. Если 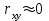 (угол между прямыми наилучших линейных регрессий близок к прямому), связь между случайными величинами достаточно слабая и нелинейная. Если (угол между прямыми наилучших линейных регрессий близок к прямому), связь между случайными величинами достаточно слабая и нелинейная. Если 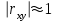 (угол близок к нулю), то связь сильная и близка к линейной. В случае промежуточного значения rxy (и угла) связь достаточно сильна и существенно нелинейная. (угол близок к нулю), то связь сильная и близка к линейной. В случае промежуточного значения rxy (и угла) связь достаточно сильна и существенно нелинейная. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
