А. П. Господариков, И. А. Лебедев
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
1.2. Повторение независимых опытовИспытания называются независимыми, если результаты любого испытания не зависят от результатов других испытаний. Формула Бернулли. Пусть производится n независимых испытаний в одинаковых условиях и каждое испытание имеет только два исхода: событие A (успех) или событие Ā (неуспех). Вероятность появления события A (успех) при одном испытании обозначим 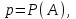 а вероятность неуспеха обозначим а вероятность неуспеха обозначим 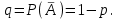 Вероятность Вероятность 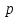 постоянна во всех испытаниях и отлична от нуля и единицы. Вероятность того, что при постоянна во всех испытаниях и отлична от нуля и единицы. Вероятность того, что при 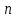 повторных испытаниях успех произойдет ровно повторных испытаниях успех произойдет ровно 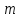 раз, определяется по формуле Бернулли: раз, определяется по формуле Бернулли: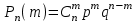 . .Вероятность 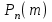 сначала увеличивается при изменении m от нуля до некоторого значения сначала увеличивается при изменении m от нуля до некоторого значения 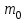 , а затем уменьшается при изменении , а затем уменьшается при изменении 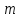 от от 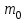 до до 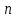 . Величина . Величина 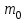 называется наивероятнейшим числом наступления события A в называется наивероятнейшим числом наступления события A в 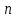 испытаниях и удовлетворяет условию: испытаниях и удовлетворяет условию: 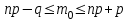 . При целом значении . При целом значении 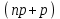 имеются два значения: имеются два значения: 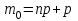 и и 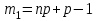 ; принецелом значении одно – ; принецелом значении одно – 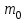 . .Вероятность хотя бы одного успеха в nнезависимых испытаниях, произведенных в одинаковых условиях, 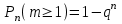 . .Для приближенного вычисления вероятностей 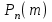 применяют предельные теоремы Муавра – Лапласа и Пуассона. применяют предельные теоремы Муавра – Лапласа и Пуассона.Локальная теорема Муавра – Лапласа. Если число независимых испытаний, производимых в одинаковых условиях, достаточно велико, и вероятность p появления события Aв каждом испытании постоянна и отлична от нуля и единицы, то вероятность 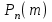 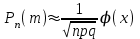 , ,где 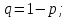 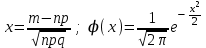 ; ; 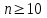 . .Отметим, что функция Гаусса (х) – четная и для нее составлены таблицы (прил.1). Вероятность появления события A в 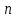 независимых испытаниях не менее независимых испытаниях не менее 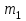 и не более и не более 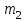 раз раз 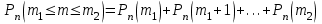 . .При большом числе испытаний 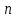 вероятность вероятность 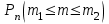 находят с помощью интегральной теоремы Муавра – Лапласа. находят с помощью интегральной теоремы Муавра – Лапласа.Интегральная теорема Муавра – Лапласа. Если число испытаний 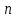 достаточно велико и вероятность достаточно велико и вероятность 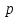 появления события A в каждом испытании постоянна и отлична от нуля и единицы, то вероятность появления события A в каждом испытании постоянна и отлична от нуля и единицы, то вероятность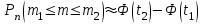 , ,где 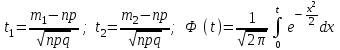 ; ; 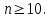 функция Лапласа Ф(t) – нечетная и для нее составлены таблицы (прил.2). Теорема Бернулли. Если в n независимых испытаниях вероятность появления события A постоянна для каждого испытания и отлична от нуля и единицы, то при достаточно большом числе испытаний с вероятностью как угодно близкой к единице (практически достоверной) относительная частота события A будет сколь угодно мало отличаться от его вероятности. Например, из интегральной теоремы Муавра – Лапласа следует, что для любого 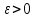 ( (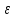 – малое положительное число) имеет место формула – малое положительное число) имеет место формула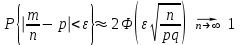 . .Закон Пуассона. Пусть число n независимых испытаний велико, вероятность 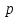 появления события A в каждом испытании постоянна и представляет малое число. Тогда при появления события A в каждом испытании постоянна и представляет малое число. Тогда при 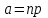 (среднее число появлений события в (среднее число появлений события в 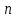 испытаниях) имеем приближенную формулу вероятности редких событий: испытаниях) имеем приближенную формулу вероятности редких событий: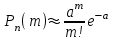 . .Такое событие A называют редким событием, а закон распределения Пуассона – законом редких событий. Пример 7. Производятся четыре независимых выстрела по мишени. Вероятность попадания в мишень при одном выстреле постоянна и равна 0,8. Найти вероятность: двух попаданий в мишень; не менее двух попаданий в мишень. Решение. По условию имеем число выстрелов 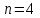 , вероятность попадания в мишень при одном выстреле , вероятность попадания в мишень при одном выстреле 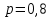 ; тогда вероятность промаха при одном выстреле ; тогда вероятность промаха при одном выстреле 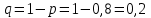 . . Вероятность двух попаданий в мишень при четырех выстрелах: 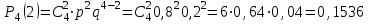 . . Не менее двух попаданий в мишень при четырех выстрелах означает два или три, или четыре попадания в мишень. Вероятность не менее двух попаданий в мишень 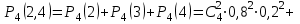 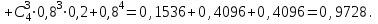 Пример 8. При установившемся технологическом процессе из 100 изготовленных деталей 10 деталей имеют дефект. Найти вероятность того, что среди 80 изготовленных деталей семь будут иметь дефект. Решение. В этой задаче испытание состоит в проверке каждой детали на наличие дефекта. Пусть событие A – обнаружение дефекта при проверке детали. По условию задачи вероятность события A в каждом опыте постоянна и равна 0,1. Так как число опытов велико, искомую вероятность находят с помощью локальной теоремы Муавра – Лапласа. Итак, 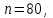 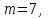 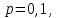 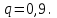 Тогда 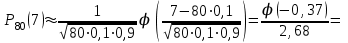 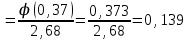 . .При вычислении учтена четность функции Гаусса, а ее значение взято из прил.1. Пример 9. Вероятность изготовления стандартной детали на автоматическом станке равна 0,8. Найти вероятность того, что среди 100 деталей будет от 68 до 90 стандартных деталей. Решение. Здесь испытание состоит в проверке, является ли каждая деталь стандартной. Так как вероятность обнаружения стандартной детали в каждом опыте постоянна и равна 0,8, то по условию задачи 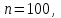 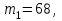 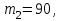 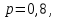 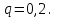 Согласно интегральной теореме Муавра – Лапласа, получим Согласно интегральной теореме Муавра – Лапласа, получим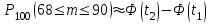 , ,где 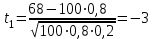 ; ; 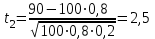 . .значения функции Лапласа (прил.2) 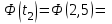 0,4938, 0,4938, 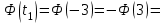 –0,49865. Окончательно получим –0,49865. Окончательно получим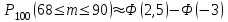 = 0,4938 + 0,49865 = 0,99245. = 0,4938 + 0,49865 = 0,99245. |
