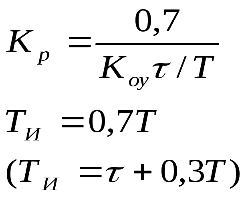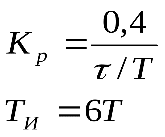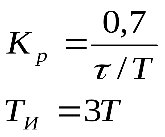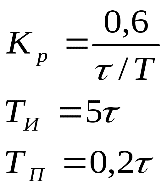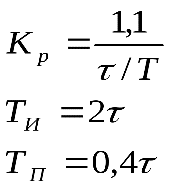нн. вопросы заказ. Автоматизация газоперекачивающих агрегатов с газотурбинным приводом компрессорных станций магистральных газопроводов

• Название: Автоматизация газоперекачивающих агрегатов с газотурбинным приводом компрессорных станций магистральных газопроводов
• Дата: 12.04.2023
• Размер: 2.14 Mb.
• Имя файла: вопросы заказ.docx
• Тип: Документы; #1056722
• страница: 9 из 9

11. ПЛК в автоматизации опасных промышленных объектов.

Этот класс микропроцессорных ПТК превосходит большинство сетевых комплексов контроллеров по мощности и сложности выполняемых функций. В целом, этот класс еще имеет ряд ограничений по объему автоматизируемого производства (порядка десятка тысяч входов/выходов) и набору реализуемых функций. Основные отличия от предшествующего класса заключаются в несколько большем разнообразии модификаций контроллеров, блоков ввода/вывода, большей мощности центральных процессоров, более развитой и гибкой сетевой структуре. Как правило, ПТК этого класса имеет развитую многоуровневую сетевую структуру. Так нижний уровень может выполнять связь контроллеров и рабочей станции компактно расположенного технологического оборудования, а верхний уровень поддерживать взаимодействие нескольких узлов друг с другом и с рабочей станцией диспетчера всего автоматизируемого участка производства. На верхнем уровне (уровне рабочих станций операторов) эти комплексы, по большей части, имеют достаточно развитую информационную сеть. В некоторых случаях расширение сетевой структуры идет в направлении применения стандартных цифровых полевых сетей, соединяющих отдельные контроллеры с удаленными от них блоками ввода/вывода и интеллектуальными приборами. Подобная простая и дешевая сеть соединяет по одной витой паре проводов контроллер с множеством интеллектуальных полевых приборов, что резко сокращает длину кабельных сетей на предприятии и уменьшает влияние возможных помех, поскольку исключается передача низковольтной аналоговой информации на значительные расстояния.

Мощность контроллеров, применяемых в этом классе средств, позволяет в дополнение к типовым функциям контроля и управления реализовывать более сложные и объемные алгоритмы управления (например, самонастройку алгоритмов регулирования, адаптивное управление). Маломасштабные распределенные системы управления используются для автоматизации отдельных средних и крупных технологических объектов предприятий непрерывных отраслей промышленности, а также цехов и участков дискретных производств и цехов заводов черной и цветной металлургии.


указать показатели качества переходного процесса САР.

Критерии оценки качества:

-Точность системы в установившемся состоянии

-Качество переходного процесса

Примечание: устойчивость не входит в показатели качества.

Типы оценок качества переходного процесса:

-Корневые

-Интегральные

-Частотные

Качество переходного процесса - определяется как реакция системы на единичное ступенчатое воздействие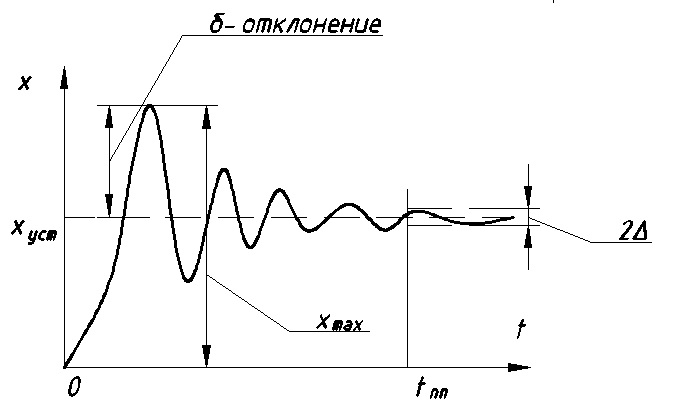



Рис. 13.1

Процесс считается завершенным, когда он входит в туннель (см. Рис.22) 2∆, где 

На практике принимается 

Показатели качества переходного процесса

1.Время переходного процесса

2.величина перерегулирования δ



· Для монотонного процесса δ=0.

· Для колебательного процесса 

3.Число колебаний за время переходного процесса

4.Плавность процесса - ограничение по максимальной скорости или ускорению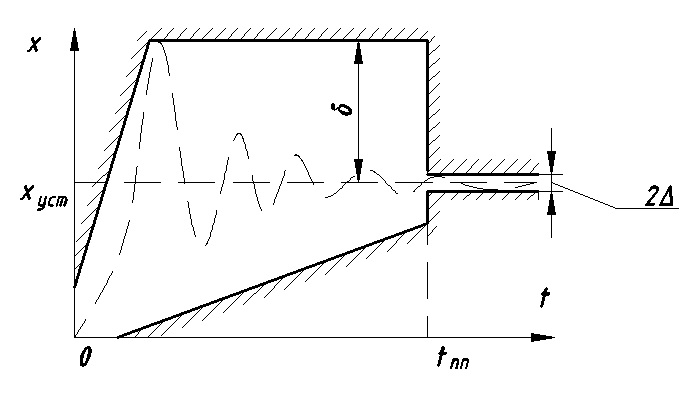



Рис. 13.2

Переходный процесс не должен выходить за вычерченную область (см. Рис.13.2).

Корневые оценки переходного процесса.

Корни характеристического уравнения определяют вид переходного процесса, также по ним можно судить о качестве переходного процесса:

Степень устойчивости - расстояние от мнимой оси до ближайшего корня (см.рис. 13.3).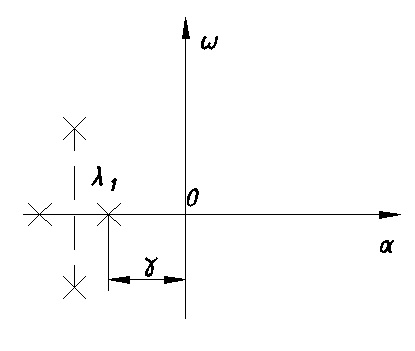



Рис. 13.3

Собственное решение характеристического ДУ:



Переходный процесс в этом случае имеет вид (см. Рис. 13.4):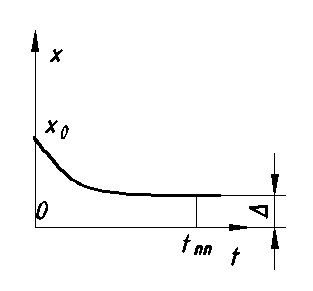



Рис. 13.4

Прологарифмируем это выражение:



Длительность переходного процесса:



При   получается:



Доминирующей составляющей решения будет колебательная составляющая:



Для аргумента φ можно получить следующее выражение (см. Рис. 13.5):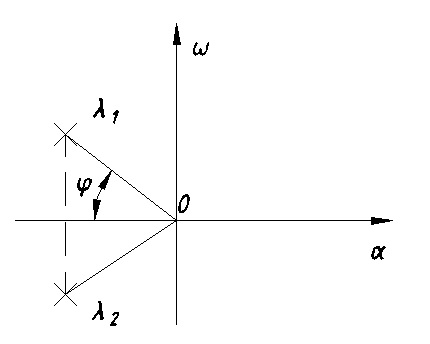





Рис. 13.5

Период колебаний вычисляется по следующей формуле:



Для определения качества колебательного переходного процесса нужно определить амплитуду через 1 период:



Колебательность процесса: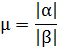



Чем меньше колебательность, тем быстрее затухает процесс.

Область допустимых значений характеристического уравнения: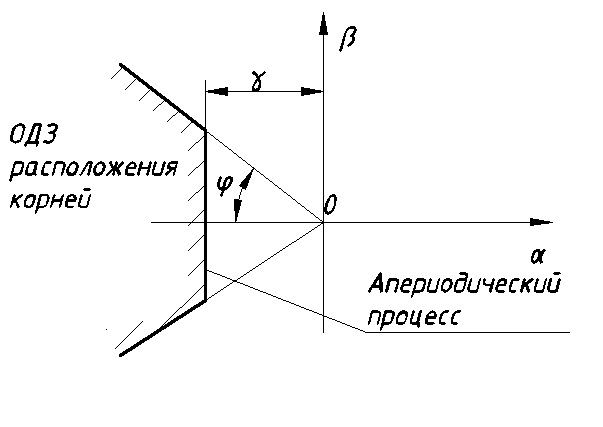



Рис. 13.6

Интегральные оценки качества

Данные критерии используются с целью общей оценки времени затухания переходных процессов и величины отклонения.

Для монотонного процесса (Рис. 13.7) интегральный критерий определяется по следующей формуле: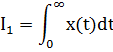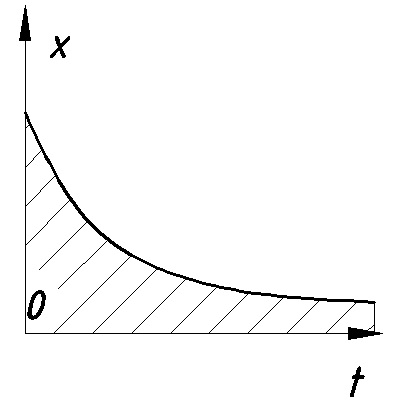





Рис. 13.7

Задача состоит в сведении данного критерия к минимуму.

Для колебательного процесса (Рис. 13.8) интегральный критерий определяется по следующей формуле с целью учета той части графика, который находится под осью абсцисс: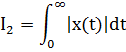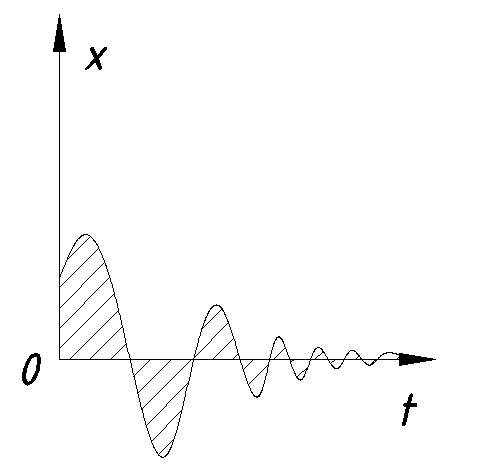





Рис. 13.8

Возможно применение следующей формулы: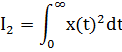



Однако данные критерии не учитывают скачки по скорости и ускорению. Поэтому используется улучшенная квадратичная оценка, которая учитывает быстро затухающие переходные процессы и их плавность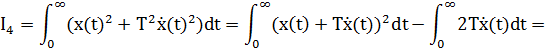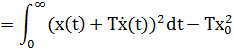





Условие минимума:



 – процесс приближается к экспоненциальному с заданным временем Т.

Частотный критерий качества

Определение запасов по устойчивости по годографу разомкнутой функции (Рис. 13.9):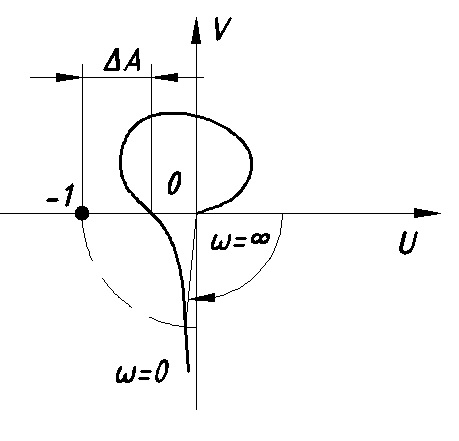



Рис. 13.9

Определение запасов по устойчивости по логарифмическим частотным характеристикам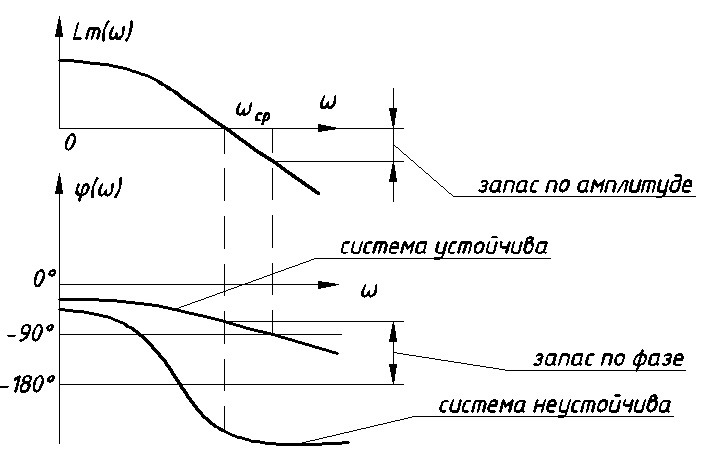



Рис. 13.10

Для определения запаса устойчивости по фазе, нужно измерить расстояние от ЛФЧХ при частоте среза до -180 градусов (см. Рис 13.10). Если система устойчива, то:



На практике часто требуется запас по фазе > 45 градусов

Для определения запаса по амплитуде необходимо для точки, где ЛФЧХ равна нулю, определить расстояние от ЛАЧХ до оси абсцисс - ЛАЧХ должна в точке этой под осью абсцисс быть (см. Рис. 13.10).

На практике часто требуется запас по амплитуде> 12 дБ

Передаточная функция замкнутой системы:



Подаем на вход системы g(t)=1(t)

На входе получаем x(t)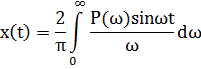





Чаще всего используются приближенные методы оценки для определения длительности процесса.

Определение области существенных частот и величины перерегулирования (Рис. 13.11):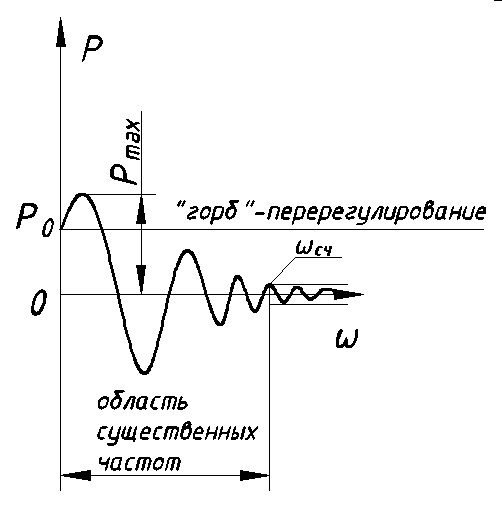



Рис. 13.11

Область существенных частот заканчивается, когда переходный процесс входит в туннель 0.05P₀.

При величине перерегулирование   «горба» нет (Рис. 13.12).

При монотонном процессе величина перерегулирование равна нулю (Рис. 13.13).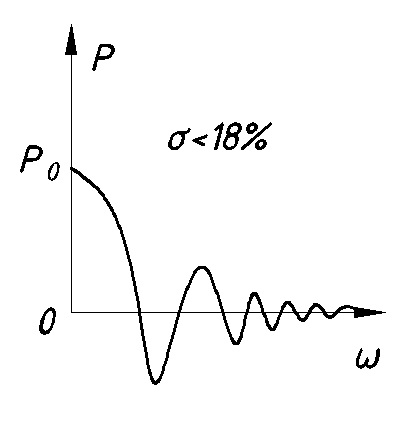



Рис. 13.12 – «горба» нет.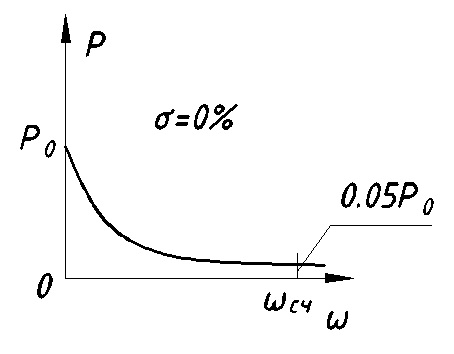



Рис. 13.13 – при монотонном процессе

перерегулирование равно нулю

Выделяют три области частоты (Рис. 13.14):

-Низкие частоты

-Средние частоты

-Высокие частоты

Область низких частот влияет на точность, область высоких частот влияет на устойчивость, область высоких влияет на фильтрующие свойства системы.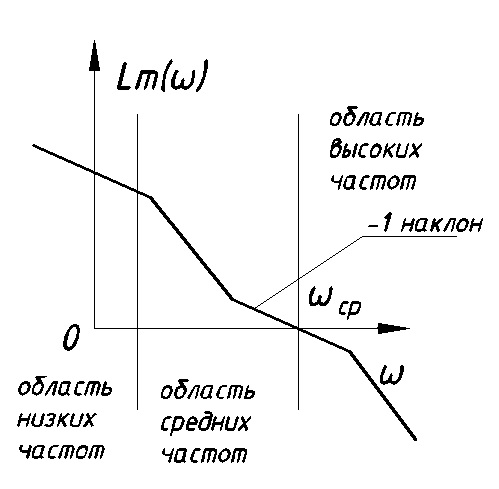



Рис. 13.14

Примечание: чем больше область существенных частот, тем меньше время переходного процесса

Время переходного процесса в зависимости от   оценивается следующим образом:



Примечание: в области средних частот важен наклон ЛАЧХ. Если наклон ЛАЧХ при   равен -20 дБ/дек, то система, скорее всего, имеет свойства монотонности. Если при   наклон равен -40 дБ/дек, то, вероятно, система имеет колебательные свойства.

Можно определить частоту среза при помощи примерных зависимостей между 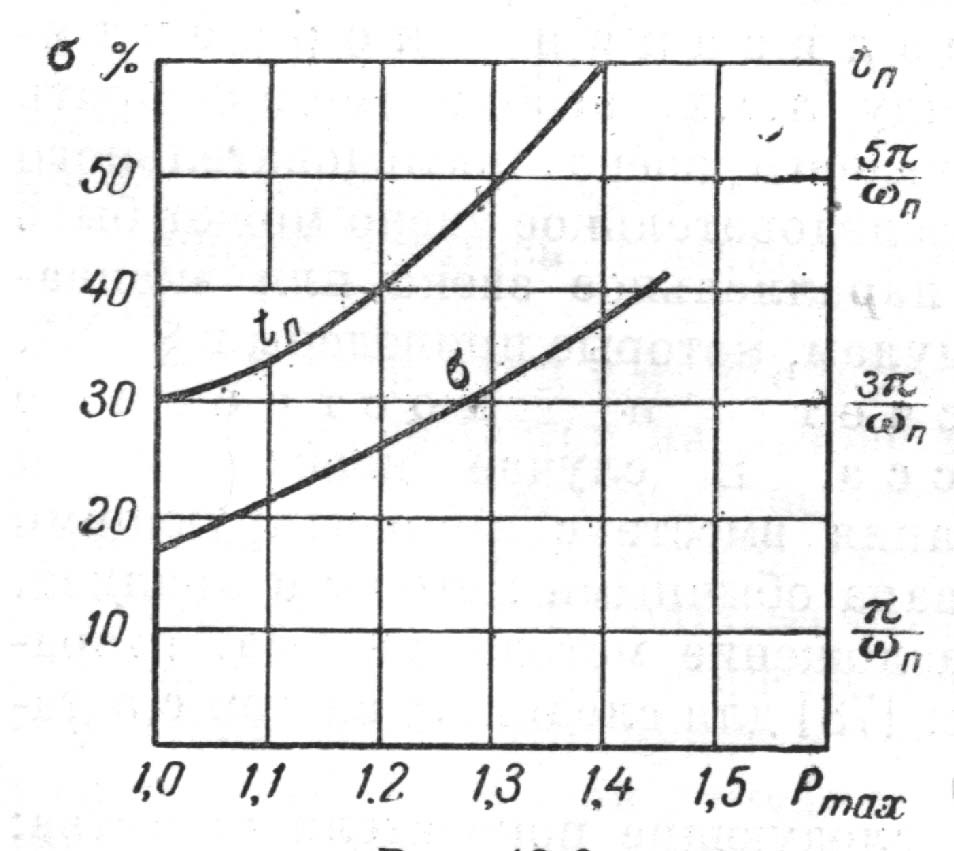  – используется номограмма (Рис. 13.15):



Рис. 13.15 Номограмма


Задача

Для определения параметров k, Т_И для ПИ- и k, Т_И, Т_Пдля ПИД- регуляторов можно использовать различные методы, мы подробнее остановимся на формульном методе определения настроек регулятора.

Формульный метод определения настроек регулятора используется для быстрой, приближенной оценки значений параметров настройки регулятора для трех видов оптимальных типовых процессов регулирования.

Метод применим как для статических объектов с самовыравниванием (таблица 7), так и для объектов без самовыравнивания (таблица 8).

Таблица 7 - Параметры настройки регуляторов для объектов с

самовыравниванием

Регулятор	Типовой процесс регулирования
	апериодический	с 20% перерегулированием
И
П
ПИ

где T, τ,  - постоянная времени, запаздывание и коэффициент усиления объекта.

В этих формулах предполагается, что настраивается регулятор с зависимыми настройками, передаточная функция которого имеет вид:

,

где  - коэффициент усиления регулятора;

- время изодрома (постоянная интегрирования регулятора);

- время предварения (постоянная дифференцирования).

Таблица 8 - Параметры настройки регуляторов для объектов

без самовыравнивания

Регулятор	Типовой процесс регулирования
	апериодический	с 20% перерегулированием
П
ПИ
ПИД

Когда параметры настройки регулятора определены, используя формулу 4, запишем передаточные функцию регулятора.

с учетом типового процесса регулирования

Рассматриваемый объект управления обладает самовыравниванием и аппроксимируется апериодическим звеном 1-го порядка. Исходя из этого, в качестве типового примем апериодический процесс.

Параметры регулятора определим из формулы: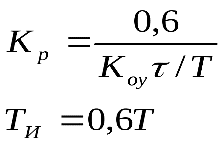



Тогда K_p=5,4; T_и=5,4.

Таким образом, передаточная функция ПИ- регулятора примет вид:

.

типового процесса регулирования

Параметры регулятора определим из формул: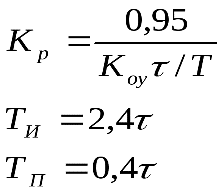



К_р=8,59; Т_и=4,8; Т_п=0,8

Тогда передаточная функция ПИ- регулятора примет вид:

.

Понятиеустойчивости является важнейшей качественной оценкой динамических свойств САР. Способность системы восстанавливать состояние равновесия, из которого она была выведена в результате какого-либо воздействия, называется устойчивостью. В зависимости от характера переходного процесса различают три основных случая поведения или изменения заданного значения регулируемой величины:

• 
  если с течением времени после окончания переходного процесса система приходит в первоначальное или другое установившееся состояние, то такой переходный процесс будет сходящимся, а система – устойчивой;
  
• 
  если при тех же условиях система характеризуется установившимся периодическим движением, то такой переходный процесс называется незатухающим, колебательным, а система находится на границе устойчивости;
  
• 
  если система не может восстановить равновесного состояния, а значение регулируемой величины всё более отклоняется от заданного, то такой процесс называется расходящимся, а система – неустойчивой.
  

С целью упрощения анализа устойчивости систем разработано ряд специальных методов, которые получили название критерии устойчи­вости. Критерии устойчивости делятся на две разновидности: алгебраические и частотные. Алгебраические критерии являются аналитическими, а частотные - графо-аналитическими. Критерии устойчивости позволяют также оценить влияние параметров системы на устойчивость.

Следует обратить внимание на важные преимущества критерия устойчивости Найквиста по сравнению с критериями Раусса – Гурвица и Михайлова:

1. При использовании этого критерия нет необходимости в знании характеристического уравнения замкнутой системы – вся необходимая информация может быть получена экспериментально.

2. Критерий применим для систем с распределенными параметрами и транспортным запаздыванием, передаточные функции которых трансцендентны.

Теорема (критерий Найквиста). Для устойчивости САУ необходимо и достаточно, чтобы годограф разомкнутой системы  при измененииω от 0 до ∞ охватывал l/2 раз в положительном направлении точку (-1, i0), где l – число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости.

Из этой теоремы непосредственно вытекает.

Следствие. Если разомкнутая система устойчива (l=0), то для устойчивости замкнутой системы необходимо и достаточно, чтобы частотный годограф  при измененииω от 0 до ∞ не охватывал точку (-1, i0).

Заметим, что для применения частотного критерия устойчивости Найквиста необходимо знать, устойчива или неустойчива система в разомкнутом состоянии. При этом, если система в разомкнутом состоянии неустойчива, то следует определить количество корней её характеристического уравнения, имеющих положительные вещественные части. Только в этом случае можно применить частотный критерий устойчивости Найквиста к исследованию устойчивости замкнутой системы.