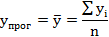
Метод среднего уровня ряда
Метод скользящих средних
Метод экспоненциального сглаживания
Метод среднего абсолютного прироста
Метод среднего темпа роста
Выберите метод простой экстраполяции основанный на следующем выражении 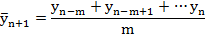
Метод скользящих средних
Метод среднего уровня ряда
Метод экспоненциального сглаживания
Метод среднего абсолютного прироста
Метод среднего темпа роста
Выберите метод простой экстраполяции основанный на следующем выражении 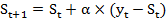
Метод экспоненциального сглаживания
Метод среднего уровня ряда
Метод скользящих средних
Метод среднего абсолютного прироста
Метод среднего темпа роста
Выберите метод простой экстраполяции основанный на следующем выражении 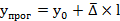
Метод среднего абсолютного прироста
Метод среднего уровня ряда
Метод скользящих средних
Метод экспоненциального сглаживания
Метод среднего темпа роста
Выберите метод простой экстраполяции основанный на следующем выражении 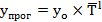
Метод среднего темпа роста
Метод среднего уровня ряда
Метод скользящих средних
Метод экспоненциального сглаживания
Метод среднего абсолютного прироста
Выберите метод кластеризации, использующий для прогноза вероятностный подход
K-средних (K-means)
Метод нечеткой кластеризации C-средних (C-means)
Нейронная сеть Кохонена
Генетический алгоритм
Построение дендрограммы с помощью дерева решений
Выберите метод кластеризации, использующий для прогноза логический подход
Построение дендрограммы с помощью дерева решений
K-средних (K-means)
Метод нечеткой кластеризации C-средних (C-means)
Нейронная сеть Кохонена
Генетический алгоритм
Выберите метод кластеризации, использующий для прогноза вероятностный подход
К-медиан (K-medians)
Метод нечеткой кластеризации C-средних (C-means)
Нейронная сеть Кохонена
Генетический алгоритм
Построение дендрограммы с помощью дерева решений
Выберите метод кластеризации, использующий для прогноза подходы на основе систем искусственного интеллекта
Метод нечеткой кластеризации C-средних (C-means)
K-средних (K-means)
К-медиан (K-medians)
Построение дендрограммы с помощью дерева решений
ЕМ – алгоритм
Выберите метод кластеризации, использующий для прогноза подходы на основе систем искусственного интеллекта
Генетический алгоритм
K-средних (K-means)
К-медиан (K-medians)
Построение дендрограммы с помощью дерева решений
ЕМ – алгоритм
Выберите графическое изображение данных, которое позволяет изобразить взаимные связи между объектами из заданного множества
Дендограмма
Пиктограмма
Скатерограмма
Гистограмма
Круговая диаграмма
В работах по кластерному анализу известен большой ряд способов построения дендрограмм. Выберите из них метод, который известен, как «метод ближайшего соседа»
метод одиночной связи
метод полной связи
метод средней связи
центроидный метод
метод Уорда
В работах по кластерному анализу известен большой ряд способов построения дендрограмм. Выберите из них метод, который известен, как «метод дальнего соседа»
метод полной связи
метод средней связи
центроидный метод
метод одиночной связи
метод Уорда
Анализ данных с применением компьютера включает выполнение ряда необходимых шагов. Первым шагом является
Определение структуры исходных данных.
Задание метода обработки данных в соответствии с задачами исследования.
Ввод данных в компьютер в соответствии с их структурой и требованиями программы. Редактирование и преобразование данных.
Получение результата обработки данных. Его редактирование и сохранение
в нужном формате.
Интерпретация результата обработки.
Анализ данных с применением компьютера включает выполнение ряда необходимых шагов. Вторым шагом является
Ввод данных в компьютер в соответствии с их структурой и требованиями программы. Редактирование и преобразование данных.
Задание метода обработки данных в соответствии с задачами исследования.
Определение структуры исходных данных.
Получение результата обработки данных. Его редактирование и сохранение
в нужном формате.
Интерпретация результата обработки.
Анализ данных с применением компьютера включает выполнение ряда необходимых шагов. Третьим шагом является
Задание метода обработки данных в соответствии с задачами исследования.
Определение структуры исходных данных.
Получение результата обработки данных. Его редактирование и сохранение
в нужном формате.
Ввод данных в компьютер в соответствии с их структурой и требованиями программы. Редактирование и преобразование данных.
Интерпретация результата обработки.
Анализ данных с применением компьютера включает выполнение ряда необходимых шагов. Четвертым шагом является
Получение результата обработки данных. Его редактирование и сохранение
в нужном формате.
Задание метода обработки данных в соответствии с задачами исследования.
Определение структуры исходных данных.
Ввод данных в компьютер в соответствии с их структурой и требованиями программы. Редактирование и преобразование данных.
Интерпретация результата обработки.
Анализ данных с применением компьютера включает выполнение ряда необходимых шагов. Пятым шагом является
Интерпретация результата обработки.
Задание метода обработки данных в соответствии с задачами исследования.
Определение структуры исходных данных.
Получение результата обработки данных. Его редактирование и сохранение
в нужном формате.
Ввод данных в компьютер в соответствии с их структурой и требованиями программы. Редактирование и преобразование данных.
Анализ данных с применением компьютера включает выполнение ряда необходимых шагов. Выберите подготовительный шаг, который не способна выполнить ни одна компьютерная программа — его исследователь делает сам.
Определение структуры исходных данных.
Задание метода обработки данных в соответствии с задачами исследования.
Получение результата обработки данных. Его редактирование и сохранение
в нужном формате.
Ввод данных в компьютер в соответствии с их структурой и требованиями программы. Редактирование и преобразование данных.
Интерпретация результата обработки.
Анализ данных с применением компьютера включает выполнение ряда необходимых шагов. Выберите заключительный шаг, который не способна выполнить ни одна компьютерная программа — его исследователь делает сам.
Интерпретация результата обработки.
Задание метода обработки данных в соответствии с задачами исследования.
Определение структуры исходных данных.
Ввод данных в компьютер в соответствии с их структурой и требованиями программы. Редактирование и преобразование данных.
Получение результата обработки данных. Его редактирование и сохранение
в нужном формате.
Расширение файла данных SPSS
*.sav
*.sps
*.spss
*.ssp
*.sta
Имя переменной в SPSS не является произвольным. Существует ряд соглашений, которым оно должно удовлетворять. Выберите, то, что относиться к этим соглашениям:
длина имени — не более 64 символов (в ранних версиях — до 8 символов)
в имени могут использоваться любые буквы, цифры, символы @, #, ., _, $
имя всегда должно начинаться с буквы, а символ «.» (точка) не может
стоять в конце имени
имена всех переменных должны быть разными
буквы верхнего и нижнего регистров символов различаются
Параметр Метка для переменной в SPSS используется
когда смысл переменной недостаточно точно отражен в названии.
для задания числа десятичных знаков после запятой в случае, если тип переменной допускает использование дробных чисел.
для задания максимальное количество знаков, которое может иметь значение переменной, включая дробную часть.
для управления наименованиями уровней (категорий) переменной.
когда требуется различать причины пропусков значений.
Параметр Ширина переменной в SPSS используется
для задания максимальное количество знаков, которое может иметь значение переменной, включая дробную часть.
когда смысл переменной недостаточно точно отражен в названии.
для задания числа десятичных знаков после запятой в случае, если тип переменной допускает использование дробных чисел.
для управления наименованиями уровней (категорий) переменной.
когда требуется различать причины пропусков значений.
Параметр Десятичные для переменной в SPSS используется
для задания числа десятичных знаков после запятой в случае, если тип переменной допускает использование дробных чисел.
когда смысл переменной недостаточно точно отражен в названии.
для задания максимальное количество знаков, которое может иметь значение переменной, включая дробную часть.
для управления наименованиями уровней (категорий) переменной.
когда требуется различать причины пропусков значений.
Параметр Метки значений переменных в SPSS используется
для управления наименованиями уровней (категорий) переменной.
когда смысл переменной недостаточно точно отражен в названии.
для задания числа десятичных знаков после запятой в случае, если тип переменной допускает использование дробных чисел.
для задания максимальное количество знаков, которое может иметь значение переменной, включая дробную часть.
когда требуется различать причины пропусков значений.
Параметр Пропуски значений переменных в SPSS используется
для управления наименованиями уровней (категорий) переменной.
когда смысл переменной недостаточно точно отражен в названии.
для задания числа десятичных знаков после запятой в случае, если тип переменной допускает использование дробных чисел.
для задания максимальное количество знаков, которое может иметь значение переменной, включая дробную часть.
когда требуется различать причины отсутствующих значений.
Шкала, содержащая только категории; данные в ней не могут упорядочиваться, с ними не могут быть произведены никакие арифметические действия
Номинальная шкала
Порядковая шкала
Шкала интервалов
Шкала отношений
Абсолютная Шкала
Шкала, в которой числа присваивают объектам для обозначения относительной позиции объектов, но не величины различий между ними
Порядковая шкала
Номинальная шкала
Шкала интервалов
Шкала отношений
Абсолютная Шкала
Из количественных шкал наиболее распространенной в науке и практике является
Шкала отношений
Номинальная шкала
Порядковая шкала
Шкала интервалов
Абсолютная Шкала
Только для этойшкалы результаты измерений - числа в обычном смысле слова
Абсолютная Шкала
Номинальная шкала
Порядковая шкала
Шкала интервалов
Шкала отношений
Шкала стадий гипертонической болезни (по Мясникову) относится к
Порядковой шкале
Номинальной шкале
Шкале интервалов
Шкале отношений
Абсолютной Шкале
Шкала степеней сердечной недостаточности (по Стражеско-Василенко-Лангу) относится к
Порядковой шкале
Номинальной шкале
Шкале интервалов
Шкале отношений
Абсолютной Шкале
Шкала степени выраженности коронарной недостаточности (по Фогельсону) относится к
Порядковой шкале
Номинальной шкале
Шкале интервалов
Шкале отношений
Абсолютной Шкале
Шкала, построенная по схеме: заболевание не обнаружено; первая стадия заболевания; вторая стадия; третья стадия относятся к
Порядковой шкале
Номинальной шкале
Шкале интервалов
Шкале отношений
Абсолютной Шкале
При описании групп инвалидности используют шкалу
Порядковую
Номинальную
Интервалов
Отношений
Абсолютную
В этой шкале есть естественное начало отсчета - нуль, т.е. отсутствие величины, но нет естественной единицы измерения.
Шкала отношений
Номинальная шкала
Порядковая шкала
Шкала интервалов
Абсолютная Шкала
По этой шкале измерены большинство физических единиц, например масса тела
Шкала отношений
Номинальная шкала
Порядковая шкала
Шкала интервалов
Абсолютная Шкала
Шкала состоит из названий, категорий, имен для классификации и сортировки объектов или наблюдений по некоторому признаку
Номинальная шкала
Порядковая шкала
Шкала интервалов
Шкала отношений
Абсолютная Шкала
По этой шкале измеряют величину потенциальной энергии или координату точки на прямой. В этих случаях на шкале нельзя отметить ни естественное начало отсчета, ни естественную единицу измерения. Исследователь должен сам задать точку отсчета и сам выбрать единицу измерения
Шкала интервалов
Номинальная шкала
Порядковая шкала
Шкала отношений
Абсолютная Шкала
Статистический метод, позволяющий получить показатели, пригодные для сравнения в двух совокупностях, неоднородных по своему составу, называется
методом стандартизации
корреляционным анализом
параметрическим методом
непараметрическим методом
регрессионным анализом
Показатели, которые могли бы быть при условии одинакового состава среды (населения, состава больных) называются
стандартизованными |
 Скачать 0.88 Mb.
Скачать 0.88 Mb.