Поведение фирмы в условиях дуополии. Модель Курно.
Дуополия.
Лучше понять закономерности поведения фирмы на олигополистическом рынке позволяет анализ дуополии, т. е. простейшей олигополистической ситуации, когда на рынке действуют только две конкурирующие между собой фирмы. Главная особенность моделей дуополий состоит в том, что выручка и, следовательно, прибыль, которую получит фирма, зависит не только от ее решений, но и от решений фирмы-конкурента, также заинтересованной в максимизации своей прибыли. Процесс принятия решения на дуополистическом рынке это когда игрок ищет самые сильные ответы на возможные варианты хода своего противника.
Модель Курно.
Существует много моделей олигополии, и ни одну из них нельзя считать универсальной, тем не менее общую логику поведения фирм на этом рынке они объясняют. Первая модель дуополии была предложена французским экономистом Огюстеном Курно еще в 1838 г.
Модель Курно анализирует поведение фирмы-дуополиста исходя из допущения, что ей известен объем выпуска продукции, который ее единственный конкурент уже выбрал для себя. Задача фирмы состоит в том, чтобы определить собственный размер производства, сообразуясь с решением конкурента как с данностью. На рис. 9.2 показано, каким было бы поведение фирмы в таких условиях.
Рис. 9.2. Поведение фирмы-дуополиста в краткосрочном периоде
Краткосрочный период
Чтобы не усложнять график, мы сделали два дополнительных упрощения. Во-первых, приняли, что оба дуополиста совершенно одинаковые, ничем не отличающиеся компании. Во-вторых, допустили, что предельные издержки обеих фирм постоянны: кривая MC идет строго горизонтально.
Допустим вначале, что фирме № 1 твердо известно, что конкурент не собирается вообще ничего выпускать. В этом случае фирма № 1 фактически является монополией. Кривая спроса на ее продукцию (D0) поэтому совпадет с кривой спроса всей отрасли. Соответственно кривая предельного дохода займет некоторое положение (MR0). Пользуясь обычным правилом равенства предельного дохода и предельных издержек MC MR, фирма № 1 установит оптимальный для себя объем производства (в изображенном на графике случае 50 ед.) и уровень цен (Р1).
А если фирме № 1 станет известно, что ее конкурент сам намерен выпустить 50 ед. продукции по цене Р1? На первый взгляд может показаться, что тем самым он исчерпает весь объем спроса и вынудит фирму № 1 отказаться от производства. Однако это не так. Если фирма № 1 установит на свою продукцию цену Р1, то спроса на нее действительно не будет: те 50 ед., которые рынок готов принять по этой цене, уже поставлены фирмой № 2. Но если фирма № 1 установит цену Р2, то общий спрос рынка составит 75 ед. (см. кривую спроса отрасли D0). Поскольку фирма № 2 предлагает только 50 ед., то на долю фирмы № 1 останется 25 ед. (7550 25). Если же цена будет опущена до Р3, то, повторив аналогичные рассуждения, можно установить, что потребность рынка в продукции фирмы № 1 составит 50 ед. (10050 50). Легко понять, что перебирая разные возможные уровни цен, мы будем получать и разные уровни потребности рынка в продукции фирмы № 1. Иными словами, на продукцию фирмы № 1 сформируется новая кривая спроса (на нашем графике D1) и соответственно новая кривая предельного дохода (MR1). Снова, использовав правило MC MR, можно определить новый оптимальный объем производства (в нашем случае он составит 25 ед.).
Равновесие Курно.
Чтобы лучше уяснить все последствия этой закономерности, обратимся к рис. 9.3. По горизонтали откладываются размеры производства одной фирмы, по вертикали - другой. Размеры выпуска продукции фирмой № 1 изображены как кривая реакции на объем производства фирмы № 2. Аналогичным образом выпуск продукции фирмой № 2 представлен как функция от объема производства фирмы № 1:
Q(1) f (Q(2)), Q(2) f (Q(1)), где Q(1) объем производства фирмы № 1, а Q(2) объем производства фирмы № 2.
Рис. 9.3. Равновесие Курно 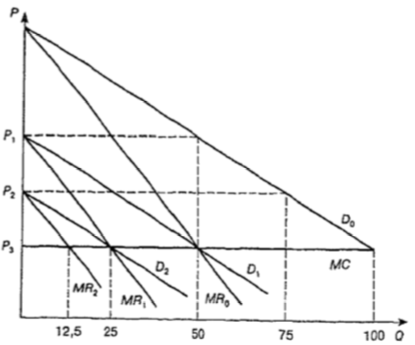
Посмотрим, смогут ли обе фирмы установить взаимоприемлемые объемы производства? Все данные для графика мы взяли из предыдущего примера. Так, если о фирме № 2 известно, что она собирается выпустить 75 ед. продукции, то фирма № 1 примет решение о выпуске 12,5 ед. (см. точку А). Но если фирма № 1 действительно выпустит 12,5 ед., то, как видно на графике, фирма № 2 в соответствии со своей кривой реакции должна выпустить не 75, а 42,5 ед. (точка В). Но такой уровень выпуска продукции конкурентом вынудит фирму № 1 выпустить не 12,5 ед., как она собиралась, а 29 ед. (точка С) и т. д. Легко заметить, что уровень производства, устанавливаемый компанией исходя из сложившегося размера производства конкурента, каждый раз оказывается таким, что заставляет последнего пересмотреть его. Это вызывает новую корректировку объема производства первой фирмы, что в свою очередь снова изменяет планы второй, т. е. ситуация является неустойчивой, неравновесной. Однако существует и точка устойчивого равновесия это точка пересечения кривых реакции обеих фирм (на графике точка О). В нашем примере, фирма № 1 выпускает 33,3 ед., исходя из того, что конкурент выпустит столько же. А для последнего выпуск 33,3 ед. действительно является оптимальным. Каждая из фирм выпускает объем продукции, максимизирующий ее прибыли при данном объеме производства конкурента. Ни одной из фирм не выгодно менять объем производства, следовательно, равновесие устойчиво. Оно получило в теории название равновесия Курно. Под равновесием Курно понимается такое сочетание объемов выпуска каждой из фирм, при котором ни у одной из них нет стимулов для изменения своего решения: прибыль каждой фирмы максимальна при условии, что конкурент сохранит данный объем выпуска. Или по-другому: в точке равновесия Курно ожидаемый конкурентами объем выпуска продукции любой из фирм совпадает с фактическим и при этом является оптимальным. Существование равновесия Курно свидетельствует о том, что олигополия как тип рынка может быть устойчивой, что она не обязательно ведет к череде непрерывных, болезненных пределов рынка олигополистами. Математическая теория игр показывает, что равновесие Курно при одних допущениях о логике поведения дуополистов достигается, а при других нет. При этом решающее значение для достижения равновесия является понятность (предсказуемость) действий партнера-конкурента и готовность его к кооперативному поведению с соперником.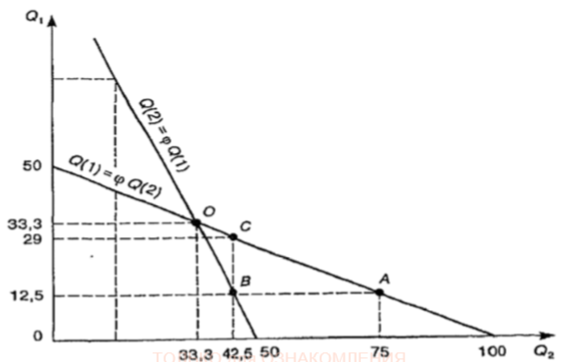
|
Поведение фирмы-монополиста в краткосрочный и долгосрочный период.
Краткосрочный период. На графике отражается процесс выбора оптимального объема производства монополистом и процесс установления рыночного равновесия в монополизированной отрасли. Объем производства установится на уровне Qm, соответствующем точке пересечения кривых предельного дохода и предельных издержек (МС=МR). Проекция этой точки на кривую спроса (точка Оm) задаст и равновесную цену Рm. Точка Оm отражает не только ценовой и количественный оптимум для фирмы, но и становится точкой общеотраслевого рыночного равновесия в условиях монополии.
При монополии степень несовершенства рынка достигает максимума.
Особенно это проявляется в том, что типичные последствия несовершенной конкуренции сказываются на этом рынке с особой силой. 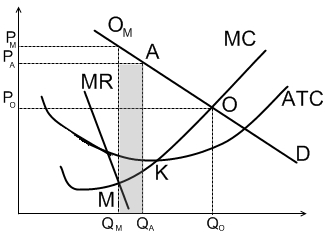
1) сильное недопроизводство товаров по сравнению с конкурентным уровнем (QM <
2) значительное завышение цен в сравнении с величиной, которая сложилась бы при совершенной конкуренции (PM>>PO)
Это происходит, потому что полное отсутствие конкурентов на рынке позволяет монополисту столь резко ограничивать предложение, что уровень цен поднимается до экономически обоснованного (с точки зрения монополиста) максимума.
Однако стоить отметить, что монополия взимает максимально возможную для неё цену, которая одновременно достаточно высока для максимизации прибыли, но достаточно низка для того, чтобы побудить потребителей приобретать максимизирующий объём производства.
Долгосрочный период. Монополист не имеет кривой предложения. Решение монополиста об изменении масштаба производства зависит только от соотношения кривых рыночного спроса и долгосрочных средних издержек. Монополист сам определяет, сколько продукции в отрасли выпускать => он может варьировать предложение, чтобы максимизировать прибыль.
Первый график: рыночный спрос не изменяется, тогда монополист переходит в долгосрочный период, если цена выше средних долгосрочных издержек.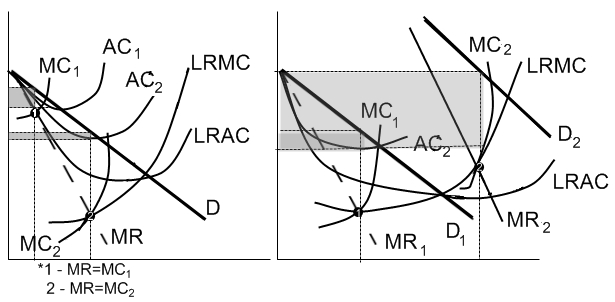
Второй график: меняется рыночный спрос (покупатели покупают больше) => формируются новые кривые => новая цена => огромная прибыль => компания переходит в долгосрочный период, если там она сможет установить цену выше, чем средние долгосрочные издержки.
|
Почему в экономике существуют такие иерархические структуры как фирмы (порой гигантские)? Ведь рынок эффективнее иерархии? Как влияют разные виды издержек на оптимальный размер фирмы? Объяснить с использованием графиков.
Фирма – это единица предпринимательской деятельности, оформленная юридически и реализующая собственные интересы посредством производства и продажитоваров и услуг с использованием различных факторов производства.
1.Фирмы существуют в экономике, потому что:
производственная деятельность в рыночной экономике осуществляется в основном фирмами;
фирмы является основным потребителем ресурсов ( ею закупаются капитальные ресурсы – сырье, материалы, оборудование…)
размерами и числом действующих в отрасли фирм определяется и диктуется структура рынка;
деятельность фирм в большой степени определяет общую эффективность рыночной экономики.
Внутренняя структуры фирмы представляет собой типичный пример иерархии. Фирма работает как целостная, слаженная система, внутри которой действует принцип подчинения служащих фирмы распоряжениям управляющего.
Фирма и рынок представляют собой альтернативные способы экономической организации. Производство может быть организовано децентрализовано, с помощью чисто рыночных отношений, но может быть использован и иерархический принцип организации, действующий внутри фирмы. Все зависит от величины внутренних (управленческих) и внешних (рыночных) трансакционных издержек.
Причины эффективности фирмы:
Экономия трансакционных издержек при проведении сложных и длительных операций (аккумулируя большое количество ресурсов на длительное время, фирма имеет возможность заменить ряд отдельных трансакций по привлечению факторов одним-единственным долгосрочным контрактом);
снижение риска недобросовестности контрагентов (фирмы заменяет операции, осуществляемые рынком, на операции внутри фирмы и вводит жесткую систему контроля за выполнением обязательств);
снижение риска использования специфических активов (перемещение активов внутрь иерархической системы создает надежную защиту специфических ресурсов от вымогательства и позволяет их владельцам быстрее адаптироваться к возможным непредвиденным изменениям);
адаптация к внезапным изменениям ситуации (приказ позволяет приобрести дополнительных рабочих на участок или точно так же можно распределить внутри компании материальные и фиансовые ресурсы).
Не смотря на то, что фирма не может полностью избавится от трансакционных издержек, осуществление деловых операций внутри фирмы предполагает меньшие затраты по сравнению с аналогичными расходами при рыночной организации. Решение сложных деловых задач с помощью рыночной формы организации является нецелесообразным. Фирмы выступает средством экономии трансакционных издержек.
Именно поэтому фирма (иерархия) эффективнее, чем рынок.
Однако вся экономика не может быть организована в виде одной гигантской фирмы. С увеличением размеров фирмы падают внешние (рыночные) трансакционные издержки, но одновременно происходит возрастание издержек на организацию управленческих трансаций внутри фирмы. Следовательно, фирма может расширяться не бесконечно, а до таких размеров, пока внутренние (управленческие) издержки меньше, чем внешние (рыночные).
2.Влияние издержек на оптимальный размер фирмы.
Выбор оптимального размера фирмы связан с оценкой всех видов издержек: и трансформационных, и трансакционных. Наилучшей будет такая институциональная структура, при которой суммарные издержки выпуска продукции достигают своего минимального значения.
Рассотрим поведение производственных, транскционных и суммарных издержек на графике:
а) Минимум производственных издержек достигается позже, чем минимум трансакционных издержек.
С точки зрения производственных параметров деятельность фирмы является эффективной в точке А. Большой выпуск позволяет достичь минимума средних долгосрочных производственных издержек (LATC (PR));
НО! в точке А работа фирмы трансакционно неэффективна (трансакционные издержки достигают наивысшей точки – х-неэффетивность: долгосрочные производственные издержки малы, однако трансакционные зашкаливают), следовательно, данный размер предприятия НЕ может быть выбран в качестве оптимального. Внутренняя бюрократия и недостаточная мотивация персонала «съедают» все чисто производственные преимущества;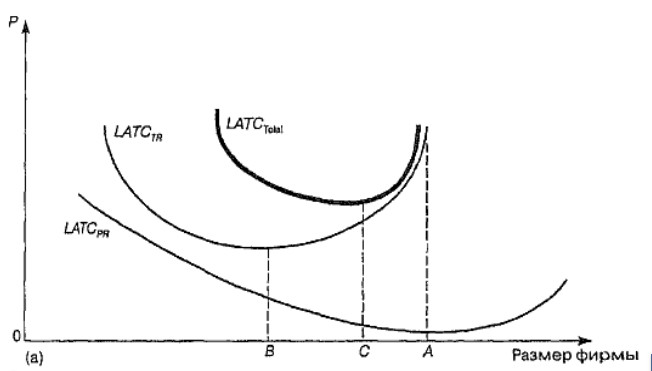
Минимум трансакционных издержек достигается в точке В, однако данный размер фирмы является неэффетивным сточки зрения производственных издержек, так как еще существует возможность снижения себестоимости за счет увеличения масштаба производства;
Следовательно, наилучший результат достигается в точке С (здесь удается минимизировать значение суммы трансформационных и трансакционных издержек (LATC (total)).
б)Минимум производственных издержек достигается раньше, чем минимум трансакционных издержек (данная ситуация на практике объясняет создание многозаводских фирм)
LATC (PR1,2) – одинаковые кривые долгосрочных производственных издержек однозаводских фирм.
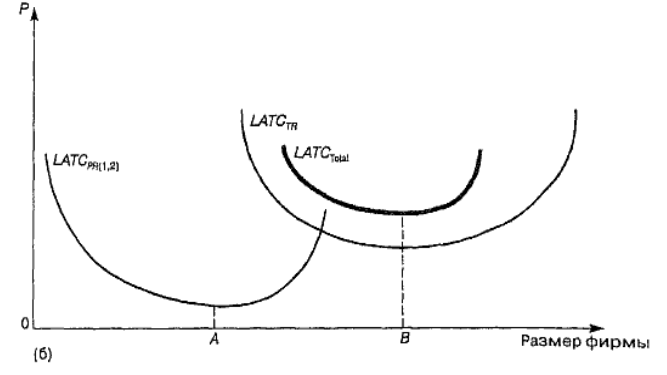
Минимум долгосрочных трансформационных издержек многозаводских фирм достигается при размере фирмы соответствующей точке А.
Однако с точки зрения трансакционных издержек был бы желателен больший размер фирмы (т. В)
В итоге оптимальной окажется многозаводсткая фирма, объединяющая несколько однозаводских фирм с целью достичь минимума трансакционных издержек. При том же размере фирмы будет достигнут и миимум общих долгосрочных издержек LATC (total), равный величине трансакционных затрат, увеличенной на минимальный размер производственных затрат однозаводской фирмы.
|
Почему инвестирование невозможно без использования процедуры дисконтирования? Назовите критерии экономической обоснованности инвестиционного проекта.
Фактор времени Основной капитал является производственным фактором длительного пользования: его участие в хозяйственной деятельности фирмы продолжается в течение нескольких лет, а то и десятилетий с момента приобретения. В связи с этим особую важность в функционировании рынка основного капитала приобретает фактор времени.
В самом деле, деятельность любого производителя сопряжена с необходимостью осуществления капиталовложений, или инвестиций расходования денежных средств в данный момент в расчете получить определенный доход в будущем. Чтобы принять разумное решение о покупке оборудования или строительстве новой очереди завода, фирме нужно сравнить предстоящие затраты с отдачей, которая будет получена благодаря им.
Принципиальное значение здесь имеет то, что затраты и доходы, связанные с инвестициями, имеют разную временную локализацию. Расходы следует сделать уже в настоящее время, а доходы они принесут лишь в будущем. Следовательно, для принятия обоснованного инвестиционного решения следует уметь сопоставлять текущую стоимость (сегодняшние затраты) с будущей стоимостью (потенциальные доходы). Каким же образом решается проблема измерения «современной стоимости будущих доходов»?
С экономической точки зрения одинаковые суммы, имеющие разную временную локализацию, отличаются по размерам. Действительно существование в экономике прибыльных вариантов инвестирования денежных средств дает возможность получать доход от любой имеющейся в настоящий момент суммы. Доходы же будущих периодов вплоть до своего реального поступления дополнительную прибыль приносить не могут.
Сущность дисконтирования
Сопоставлять денежные суммы, получаемые в разное время, позволяет разработанный экономистами метод дисконтирования. Подобно мосту, соединяющему два противоположных берега, дисконтирование делает возможным сравнение денежных потоков, получаемых в разное время, путем приведения (пересчета) их к одному временному периоду.
Итак, мы установили, что одна и та же сумма денежных средств будет иметь большую ценность в данный момент времени по сравнению с будущим. Следовательно, для обеспечения сопоставимости текущих и будущих доходов нужно скорректировать будущие поступления в сторону уменьшения. Процедура дисконтирования как раз и состоит в уменьшении будущего дохода. Чтобы научиться определять количественные масштабы этого уменьшения, необходимо рассмотреть механизм образования будущего дохода.
Предположим, что в нашем распоряжении имеется 100 000 руб. При этом есть возможность вложения данной суммы на банковский счет, ставка по которому составляет 10% годовых. Тогда будущая стоимость инвестируемых нами сегодня 100 000 руб. через год составит 110 000 руб.:
Спустя 2 года текущая сумма возрастет до 121 000 руб.: 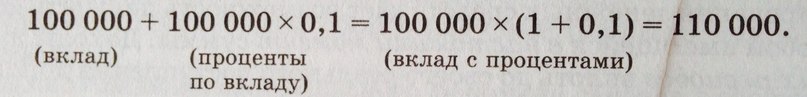
110 000 110 000 0,1 110 000 (1 0,1) 100 000 (1 0,1)2 121 000.
Через 3 года наш доход составит 133 100 руб.:
121 000 121 000 0,1 100 000 (1 0,1)3 133 100.
Легко понять, что в общем виде формула расчета будущего дохода будет:
TRn PDV (1 i)n, (формула 12.1)
где TRn совокупный доход n-го года; PDV текущая стоимость; n число лет; i процентная ставка.
Текущая дисконтированная стоимость
Формула (12.1) позволяет рассчитать будущий совокупный доход сегодняшних капиталовложений. Используя ее, мы также можем решить обратную задачу: определить текущую стоимость будущего дохода
PDV 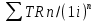
или
PDV TRn Kd, (12.2)
где Kd 1/(1 i )n коэффициент дисконтирования.
Величину PDV, полученную путем умножения совокупного будущего дохода на коэффициент дисконтирования, еще называют текущей дисконтированной стоимостью будущего дохода, поскольку коэффициент дисконтирования позволяет уравнять будущую и текущую стоимости. А так как численное значение коэффициента дисконтирования всегда меньше единицы, то уравнивание происходит за счет уменьшения будущего совокупного дохода на величину, обратно пропорциональную ставке процента.
Текущая дисконтированная стоимость (PDV) инвестиционного фонда
До сих пор мы анализировали довольно редкую ситуацию, при которой капитал инвестируется на длительный срок, а все доходы получаются единовременно по его окончании. В реальных инвестиционных проектах чаще реализуется иная схема: доходы порциями поступают в течение всего срока осуществления проекта.
Пусть, например, некая фирма приобретает мощный компьютер (сервер) стоимостью 1 млн руб. Согласно бизнес-плану, сменить его более новой машиной предполагается через 3 года, а за это время в результате его внедрения будут получены следующие суммы валового (т. е. включающего амортизацию) дохода: в 1-й год 400 тыс., во 2-й 800 тыс., в 3-й 200 тыс. руб. В этом случае текущая дисконтированная стоимость всего проекта будет складываться из суммы дисконтированных стоимостей доходов каждого года:
PDVпроекта PDV1 PDV2 PDV3 TR1 / (1 i)1 TR2 / (1 i)2 TR3 / (1 i)3.
Если принять, как и в прошлом примере, ставку процента за 10%, то в численной форме текущая дисконтированная стоимость составит:
PDVпроекта 400 / 1,1 800 / 1,21 200 / 1,311 363,6 661,2 152,6 1177,4 тыс. руб.
В общем же виде формула текущей дисконтированной стоимости проекта, длящегося n лет, выглядит: PDVпроекта PDV1 PDV2 ... PDVn. (формула 12.3)
PDV фиксированного дохода в бесконечном периоде
Еще один важный случай оценка PDV проекта, когда доход постоянен по величине и выплачивается неограниченное число лет. В чистом виде такая ситуация типична для некоторых видов ценных бумаг так называемых бессрочных облигаций и привилегированных акций (см. 14.3). При их выпуске прямо оговаривается, что вложив некоторую сумму в определенную фирму, вы приобретаете право на стабильный доход на все время, пока существует эта компания.
Присмотримся внимательно к формуле (12.3). Даже если число n будет стремиться к бесконечности, PDVпроекта составит конечную величину. Дело в том, что чем дальше в будущее отдален некоторый фиксированный доход, тем меньшую величину он составляет. Ведь:
PDVn TRconst / (1 i)n.
Числитель этой дроби по условиям выпуска названных ценных бумаг постоянен, а знаменатель с каждым годом возрастает, причем очень быстро (по экспоненте). Поэтому реальный вклад в величину PDVпроекта могут внести только несколько первых членов суммы, входящей в формулу (12.3). Все же последующие пренебрежительно малы и почти ничего к ней не добавляют. Математики называют ряды такого вида бесконечно убывающей геометрической прогрессией и давно вывели формулу для определения ее величины:
PDVбеск.проекта TRconst / i (формула 12.4)
Именно так может быть подсчитана цена привилегированной акции или бессрочной облигации, ибо все будущие доходы от нее в дисконтированной (приведенной к настоящему времени) форме составят ровно эту величину. Но, честно говоря, если бы формула (12.4) касалась только стоимости некоторых разновидностей ценных бумаг, ей вряд ли стоило бы уделять здесь место слишком уж частный это вопрос.
Гораздо важнее то, что тому же закону в основном подчиняются все относительно постоянные доходы. Например, более или менее постоянную величину составляет рента с земельного участка, арендная плата за помещение, средний уровень дивидендов по акциям и т. д. Если доход от всех этих видов имущества будет колебаться от года к году на несколько или даже на десятки процентов, формула (12.4) все равно останется применимой. В самом деле, велика ли разница, если вы делите на бесконечность, на миллион, на десять тысяч или на любое другое очень большое число доход в 100 и 150 руб.? И в том, и в другом случаях получаются доли копейки.
Поэтому на практике формула (12.4) применима ко всем случаям неограниченно долго получаемых доходов, если они колеблются не слишком сильно2. В дальнейшем мы убедимся, что по этой причине с ее помощью рассчитываются очень многие важные экономические параметры: цена земли, цена акции и т. п.
Критерий экономической обоснованности инвестиционного проекта
С помощью текущей дисконтированной стоимости мы научились приводить в соизмеримый вид произведенные затраты и получаемые в разное время доходы. Это дает возможность правильно оценить эффективность осуществляемых вложений и сделать выбор в пользу наиболее выгодного инвестиционного проекта. Показателем, позволяющим достоверно определить выгодность инвестиционного проекта, является чистая дисконтированная стоимость (NPV).
Будущий совокупный доход, приведенный к текущему периоду с помощью дисконтирования, есть текущая дисконтированная стоимость (PDVпроекта). Размер понесенных фирмой затрат отражает осуществляемые ею инвестиции (I). Очевидно, что выгода от осуществления проекта (как раз ее-то и называют чистой дисконтированной стоимостью) будет измеряться разностью обеих величин и ее можно рассчитать по формуле
NPV PDVпроекта I . (формула 12.5)
Из формулы (12.5) видно, что инвестирование будет выгодным в случае превышения получаемых доходов над произведенными вложениями, т. е. при положительном значении показателя чистой дисконтированной стоимости. Следовательно, если NPV > 0, инвестиционный проект можно считать вполне приемлемым, а вложение капитала целесообразным. В противном случае (NPV < 0) будет правильнее отказаться от намечаемого проекта, так как предполагаемые вложения не окупятся и фирма-инвестор понесет убытки.
Расчет чистой дисконтированной стоимости во многом упрощает решение стоящей перед любой фирмой сложной и одновременно жизненно важной задачи выбора наиболее выгодного инвестиционного проекта. Приведем условный пример такого расчета.
Допустим, намечаемый проект требует от предприятия вложения инвестиций в размере 20 тыс. руб. в машину, которая будет полностью амортизирована в течение четырех лет. Совокупный доход (включая амортизационные взносы), ожидаемый от данного проекта, достигнет суммы 5 тыс. руб. в 1-й и 2-й и 8 тыс. руб. в 3-й и 4-й годы. Необходимо определить выгодность проекта, учитывая, что ставка процента, составляет 10% в год. Иными словами, требуется определить чистую дисконтированную стоимость, т. е. сопоставить общие будущие поступления, приведенные к текущему периоду, и требуемые инвестиции. Решение задачи выглядит так:
NPV PDVпроекта I 5000 1 / (1 0,1) 5000 1 / (1 0,1)2 8000 1 / (1 0,1)3 8000 1 (1 0,1)4 20000 20151,4 20000 151,4 руб.
Поскольку чистая дисконтированная стоимость (NPV)в нашем примере имеет положительный знак, планируемый проект является благоприятным для фирмы. Он позволяет получить более высокий доход, чем при вложении денег в банк.
Обратим, однако, внимание и на то, насколько важное значение для принятия правильного решения имеет использование метода дисконтирования. Если бы мы действовали неправильно и просто сложили бы доходы за разные годы, как это обычно делают непрофессионалы, то проект показался бы нам очень выгодным (5000 5000 8000 8000 26000). Могло создаться впечатление, что, соглашаясь на его реализацию, мы выигрываем целых 6000 руб. В действительности выигрыш составляет лишь полторы сотни, т. е. проект находится буквально на грани приемлемости.
| |
 Скачать 3.79 Mb.
Скачать 3.79 Mb.