ШПОРЫ ОХТ. Цели и задачи курса Общая химическая технология Объект изучения курса
 Скачать 3.94 Mb. Скачать 3.94 Mb.
|
|
 | Рисунок 1. Зависимость теплот выделения qpи qT от температуры на поверхности Tnдля процесса взаимодействия газа и твердой частицы. Точки пересечения 1,2,3 соответствуют разным стационарным режимам. |
Пересечение кривых на графике зависимостей qT(Tn) иqp(Tn) ,будет решением уравнения (13). Зависимость qp(Tn) имеет вид S – образной кривой.
При малых значениях температур, когда k/β3<<1, qp(Tn) ∆Tад ·
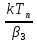 , - функция принимает вид, подобный экспоненциальной функции. При больших значениях температур, когда k/β3 >>1, qp ∆Tади зависимость – прямая линия.
, - функция принимает вид, подобный экспоненциальной функции. При больших значениях температур, когда k/β3 >>1, qp ∆Tади зависимость – прямая линия.Из рисунка 1 видно, что в зависимости от значения T0(температуры в объеме) возможно одно или три пересечения зависимостей qT (Tn) cqp(Tn) , то есть одно или три решения уравнения (13).
Наличие трех решений указывает на то, что при одних и тех же условиях процесса возможны один или три стационарных режима, то есть существует неоднозначность стационарных режимов. Какой из них будет реализован зависит от предыстории процесса. Если в начале твердая частица имеет температуру Tон , близкую к температуре газа T0 то будет реализован низкотемпературный режим (точка 1 на рис.1). При этом температура и концентрация в потоке (T0и C0) и на поверхности частицы (Tnи Cn) близки друг к другу – режим кинетический. Если же вначале частица была разогрета до TOB , то установится высокотемпературный режим (точка 3 на рис. 1) с разогревом поверхности, близким к адиабатическому (см. уравнение (9)), то есть Cn<<C0 и режим – внешнедиффузионный.
Таким образом, можно выделить области существования стационарных режимов в рассматриваемом процессе. Низкотемпературные режимы существуют при T0<T0Н, высокотемпературные при T0>T0B . При T0<T0B и T0>T0Н –стационарный режим единственный. Если же T0 лежит в интервале T0B< T0<T0Н , то система будет находиться в одном из трех стационарных режимов.
Необходимо отметить, что при некоторых условиях процесса уравнение (13) будет иметь один корень, то есть при всех T0будет существовать единственный стационарный режим (см. зависимость q’p(Tn) рис. 1)
Положительная обратная связь.
Причина появления неоднозначности стационарных режимов заключается в следующем. Скорости взаимосвязанных стдий процесса (тепловыделения при химическом превращении и межфазного теплообмена зависят от температуры поверхности Tn , увеличение которой ускоряет и реакцию (k возрастает с температурой) и теплоотвод (движущая сила (Tn – T0) становится больше).
Уменьшении Tnподавляет скорости обоих стадий.
В рассматриваемом процессе есть положительная обратная связь между тепловыми стадиями процесса:
Увеличение по какой либо причине скорости тепловыделения и, следовательно, температуры поверхности Tn , приведет к увеличению теплоотвода.
Это влияние – нелинейное (S – образная зависимость тепловыделения от температуры qp(Tn) см. рис. 1)
Именно положительная обратная связь между нелинейными стадиями процесса обуславливает возможность появления неоднозначности стационарных режимов.
Проявится ли это свойство зависит, как уже указывалось, от условий процесса.
Влияние концентрации на поверхности Сnна скорости стадий различно: скорость реакции возрастает с концентрацией (rcn) , а движущая сила (C0 – Cn) и скорость массообмена, наоборот, уменьшится.
Это – отрицательная обратная связь, не приводящая к неоднозначности стационарных режимов – в изотермическом процессе такое явление не было обнаружено.
53.Критические тепловые явления в гетерогенном процессе: гистерезис стационарных режимов.
Гистерезис стационарных режимов.
Проследим изменение разогрева поверхности (Tn – T0) при постепенном повышении температуры потока T0 и выделим ряд последовательных стационарных режимов, определенных из пересечений серии прямых qT для разных температур T0с кривой тепловыделения qp
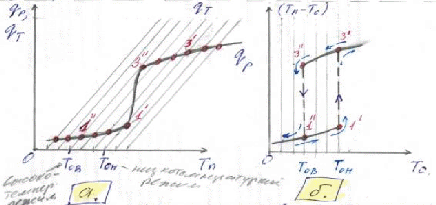 (см. рис. 2).
(см. рис. 2).| |
| Рисунок 2 : К формулировке гистерезиса стационарных режимов. |
Постепенное повышение T0приводит к постепенному увеличению Tn .
Соответствующие этим значениям режима отмечены точками внизу на рисунке 2а и кривой «1ʺ- 1ʹ» на рисунке 2б.
По достижении температуры объема системы T0 значения Toн , низкотемпературные режимы перестают существовать (последний низкотемпературный режим обозначен на рисунках 2а и 2б точкой «1ʹ») и происходит скачок в область высокотемпературных режимов. Это «температура зажигания».
Дальнейшее повышение T0будет мало влиять на разогрев поверхность (Tn-T0) который по величине близок к адиабатическому разогреву ∆Tад .
На рисунке 2б стрелками показано направление изменения (Tn-T0) с увеличением T0.
Теперь проследим за обратным движением по стрелкам с постепенным уменьшением T0, при котором стационарные режимы на рисунке 2а отмечены точками вверху. При достижении точки «3ʹ» повторяется состояние системы в высокотемпературном режиме. Причем дальнейшее уменьшение T0 приводит к реализации высокотемпературных режимов вплоть до T0В, после чего происходит переход скачком от состояния «3ʺ» к состоянию «1ʺ» (см. рисунок 2б).
T0В – граница существования высокотемпературных режимов и называется «температурой потухания»
При дальнейшем движении в сторону понижения T0 режимы будут совпадать с полученным при подъеме T0 .
Такой гистезис стационарных режимов был получен и эксперементально.
Зажигание и потухание – кристаллические режимы процесса.
Отметим, что при изменении условий процесса, например, температуры потока T0 , реализовались только низкотемпературный и высокотемпературный режимы, без среднетемпературного режима 2 (см. рис. 1)
Это связано с тем, что среднетемпературный режим является неустойчивым и на практике не реализуется.
54. Критические тепловые явления в гетерогенном процессе, практическое приминение критических режимов.
Осуществление условий ,вызывающих"зажигание процесса", можно с пользой использовать в произвдстве.
Высокотемпературный, интенсивный режимпроводится при температуре небольшой потока То.Чтобы выйти на него,
не разогревая,например катализатор и поток реагентов,на короткое время повышают концентрацию
реагента и после достижения необходимой температуры конценрацию возвращают к заданной.Таким же образом осуществляется пожигание топлива ( горение относится к процессу"газ-твердое" ).Но зажигание может привести к нежелательному самовозгоранию твердых горючих материалов.Особенно опасно это явление процессах с большим адиабатическим разогревом.Переход к высокотемпературному режиму приводит к резкому увеличению обьема газа, что приведет к тепловому взрыву.Использование критических режимов необходимо просчитать заранее ."Потухание"проесса также надо предвидеть.Например,окисление аммиакапротекает на платиноидном катализаторе во внешнедиффузионном режиме. Температура газа около 470К, катализатора-1170К,следовательно адиабатический разогрев-700 градусов.Если например ,уменьшить конценрацию аммиака(т.е.уменьшить...формула...,то будет реализован низкотемператуный режим и температура
резко спадет.Но возврат к прежним условиям по концентрации аммиака не востановит высокотемпературны режим.
Для этого будет необходим предварительный разогрев катализатора и др.пусковые операции процесса.Возможность
осуществления критических явлений необходимо учитывать в технологических работах.Основным результатом
исследования хим. процесса протекающего в элементрном обьеме,является скорость превращения компонентов реакционной смеси с учетом всех наблюдаемых в нем явлений.
55. Этапы моделирования
Процесс как теоретического, так и экспериментального моделирования состоит из следующих шагов:
Построение модели.
Изучение модели.
Экстраполяция – перенос полученных данных на область знаний об исходном объекте.
На первом этапе, при осознании невозможности или нецелесообразности прямого изучения объекта, создается его модель. Целью этого этапа является создание условий для полноценного замещения оригинала объектом-посредником, воспроизводящим его необходимые параметры.
На втором этапе производится изучение самой модели – настолько детальное, насколько это требуется для решения конкретной познавательной задачи. Здесь исследователь может вести наблюдения за поведением модели, проводить над ней эксперименты, измерять или описывать ее характеристики – в зависимости от специфики самой модели и от исходной познавательной задачи. Цель второго этапа – получение требуемой информации о модели.
Третий этап (экстраполяционный) представляет собой «возвращение» к исходному объекту, т.е. интерпретацию полученных знаний о модели, оценку их приемлемости и, соответственно, приложение их к оригиналу, позволяющее в случае успеха решить исходную познавательную задачу.
Эти шаги реализуют своеобразный цикл моделирования, в ходе которого модель и оригинал соотносятся друг с другом
Моделирование химических реакторовприменяется для предсказания результатов протекания химико-технологических процессов при заданных условиях в аппаратах любого размера. Попытки осуществить масштабный переход от реактора малого размера к промышленному реактору при помощи физического моделирования оказались безуспешными из-за несовместимости условий подобия химических и физических составляющих процесса (влияние физических факторов на скорость химического превращения в реакторах разного размера существенно различно). Поэтому для масштабного перехода преимущественно использовались эмпирические методы: процессы исследовались в последовательно увеличивающихся реакторах (лабораторная, укрупнённая, опытная, полупромышленная установки, промышленный реактор).
Исследовать реактор в целом и осуществить масштабный переход позволило математическое моделирование. Процесс в реакторе складывается из большого числа химических и физических взаимодействий на различных структурных уровнях — молекула, макрообласть, элемент реактора, реактор. В соответствии со структурными уровнями процесса строится многоступенчатая математическая модель реактора. Первому уровню (собственно химическому превращению) соответствует кинетическая модель, уравнения которой описывают зависимость скорости реакции от концентрации реагирующих веществ, температуры и давления во всей области их изменений, охватывающей практические условия проведения процесса. Характер следующих структурных уровней зависит от типа реактора. Например, для реактора с неподвижным слоем катализатора второй уровень — процесс, протекающий на одном зерне катализатора, когда существенны перенос вещества и перенос тепла в пористом зерне. Каждый последующий структурный уровень включает все предыдущие как составные части, например математическое описание процесса на одном зерне катализатора включает как уравнения переноса, так и кинетические. Модель третьего уровня включает, кроме того, уравнения переноса вещества, тепла и импульса в слое катализатора и т. д. Модели реакторов других типов (с псевдосжиженным слоем, колонного типа с суспендированным катализатором и др.) также имеют иерархическую структуру.
С помощью математического моделирования выбираются оптимальные условия проведения процесса, определяются необходимое количество катализатора, размеры и форма реактора, параметрическая чувствительность процесса к начальным и краевым условиям, переходные режимы, а также исследуется устойчивость процесса. В ряде случаев сначала проводится теоретическая оптимизация — определяются оптимальные условия, при которых выход полезного продукта наибольший, независимо от того, смогут ли они быть осуществлены, а затем, на втором этапе, выбирается инженерное решение, позволяющее наилучшим образом приблизиться к теоретическому оптимальному режиму с учётом экономических и других показателей. Для осуществления найденных режимов и нормальной работы реактора необходимо обеспечить равномерное распределение реакционной смеси по сечению реактора и полноту смешения потоков, различающихся составом и температурой. Эти задачи решаются физическим (аэрогидродинамическим) моделированием выбранной конструкции реактора.Для исследования различных процессов, в которых протекают фазовые и химические превращения, применяются методы термодинамического моделирования.Термодинамическое моделирование фазово-химических превращений основывается, с одной стороны, на законах и методах химической термодинамики, с другой - на математическом аппарате решения экстремальных задач. Полноценное сочетание этих двух подходов позволяет реализовать методику расчета, которая не имеет принципиальных ограничений на природу и компонентность исследуемых систем.
Для исследования различных практических и теоретических задач, связанных с фазовыми и химическими превращениями, необходимо глубокое и детальное исследование физико-химической сущности процесса, выявление закономерностей протекающих при этом фазовых и химических превращений, влияния на них и на выход продукта параметров состояния (температуры, давления, состава реакционной смеси и др.).
Сложность большинства реальных физико-химических процессов не позволяет решить описанные проблемы исключительно экспериментальным путем. Анализ возможных подходов показывает эффективность привлечения современных теорий и методов физико-химического и математического моделирования и расчета с использованием термодинамических представлений. C помощью данных методов можно проводить детальное исследование фазовых и химических превращений.
56. Математическая модель периодического процесса в емкостном реакторе.
Все компоненты загружают одновременно. Реакция протекает при интенсивном перемешивании, так что можно считать, что концентрация и температура по объёму
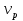 реакционной зоны( далее реактора) в каждый момент времени одинаковые.В течение процесса возможен теплообмен с теплоносителем, имеющим температуру
реакционной зоны( далее реактора) в каждый момент времени одинаковые.В течение процесса возможен теплообмен с теплоносителем, имеющим температуру 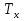 .. Площадь поверхности теплообмена обозначим
.. Площадь поверхности теплообмена обозначим 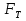 , а коэффициент теплообмена -
, а коэффициент теплообмена - 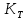 .
.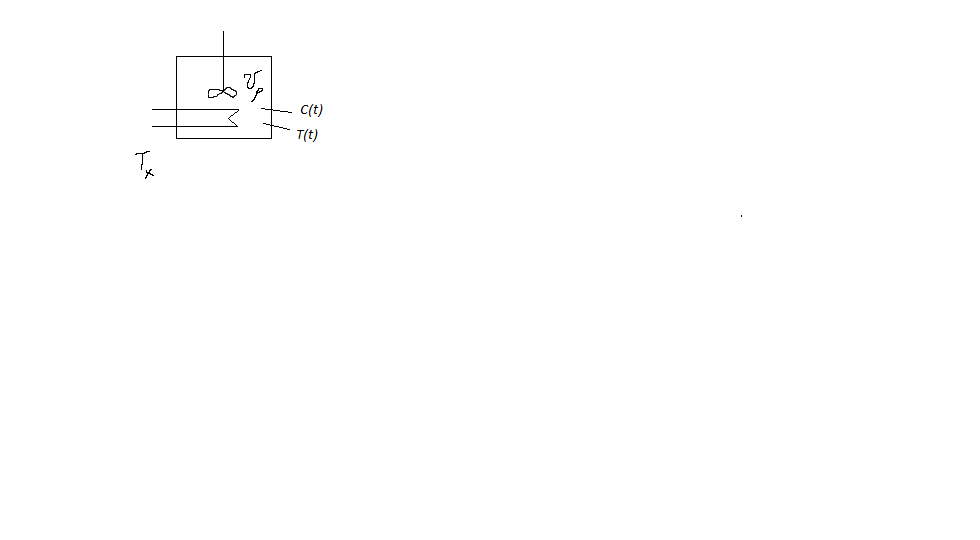
Схема процесса в таком реакторе представлена на рисунке 1:
Схема реактора в режиме идеального смешения периодическом ( ИС-n)
Процесс – нестационарный. В реакторе нет входящих и восходящих потоков и
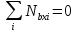 . Источником i-ого вещества является химическое превращение:
. Источником i-ого вещества является химическое превращение: 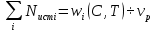
Уравнение (1) для i-ого вещества будет выглядеть следующим образом:
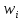 – скорость превращения i-ого вещества ;
– скорость превращения i-ого вещества ; 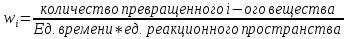 (3). Количество вещества в реакторе
(3). Количество вещества в реакторе 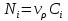 и уравнение (3) принимает вид ( в предположении, что объём реагирующей смеси равный
и уравнение (3) принимает вид ( в предположении, что объём реагирующей смеси равный 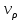 не меняется):
не меняется): (4)
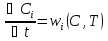
Источник теплоты – тепловой эффект химического превращения и теплообмен с теплоносителем. Для единственной реакции:
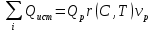
Где
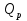 – тепловой эффект реакции ;
– тепловой эффект реакции ;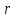 =
= 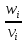 – скорость реакции
– скорость реакции 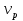 - объём реактора.
- объём реактора.Теплообмен с теплоносителем:
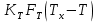 , где
, где 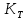 – коэффициент теплопередачи;
– коэффициент теплопередачи; 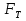 – площадь поверхности теплообмена;
– площадь поверхности теплообмена; 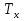 – температура теплоносителя.. Таким образом, уравнение (2) принимает вид:
– температура теплоносителя.. Таким образом, уравнение (2) принимает вид: 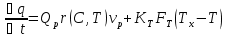 (5)
(5)Изменение количества теплоты в реакторе связано с изменением температуры в нем:
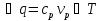 (принимаем теплоемкость
(принимаем теплоемкость 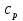 неизменной). Определим удельную поверхность теплообмена к единице объёма реактора,
неизменной). Определим удельную поверхность теплообмена к единице объёма реактора, 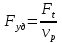 и из (5) получим:
и из (5) получим: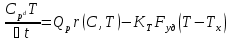 (6)
(6)Процесс начинается при концентрациях
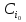 и температуре
и температуре 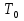 . Задаем для начала процесса начальные условия для уравнений (4) и (6)
. Задаем для начала процесса начальные условия для уравнений (4) и (6) 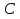 =
= 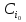 ;
; 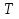 =
= 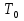 при t=0 (7) Такой процесс и описывающие его уравнения называют режимом ( моделью) идеального смешения периодическим – ИС-n.
при t=0 (7) Такой процесс и описывающие его уравнения называют режимом ( моделью) идеального смешения периодическим – ИС-n.
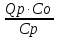 , преобразуем уравнение (4) и (5) к виду:
, преобразуем уравнение (4) и (5) к виду: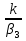 (1-xn) (10)
(1-xn) (10)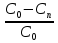 но x=
но x=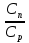 =>
=>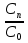 =1-x, а
=1-x, а 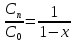 но и
но и 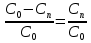 – 1 =>
– 1 =>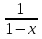 - 1 =
- 1 = 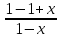 =
=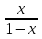 ; т.о.
; т.о. 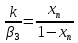 => (10) и,
=> (10) и, 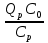 ; x=
; x= 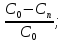 β3=
β3=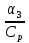 => β3Cp(Tn-T0) = Qpβ3C0
=> β3Cp(Tn-T0) = Qpβ3C0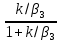 , (12)
, (12)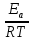 не позволяет из уравнения (13) получить значение Tnв явном виде.
не позволяет из уравнения (13) получить значение Tnв явном виде.