ШПОРЫ ОХТ. Цели и задачи курса Общая химическая технология Объект изучения курса
 Скачать 3.94 Mb. Скачать 3.94 Mb.
|
|
38.Гомогенный химический процесс: простая необратимая реакция Необратимая реакция A=R представлена химическим уравнением 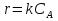 n (1), n (1),Где n – порядок реакции по A; 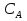 – концентрация А; r – скорость реакции. Зависимость r(CA) – концентрация А; r – скорость реакции. Зависимость r(CA)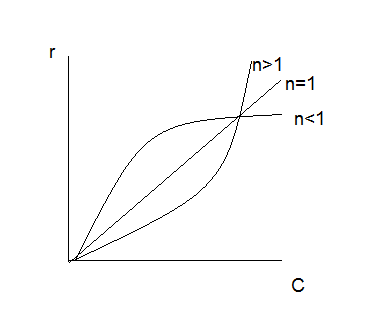 Видно, что от n зависит темп возрастания скорости – он выше для реакций более высокого порядка. Если CA выразить через степень превращения XA 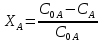 => => 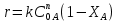 n (2) n (2)Зависимость r(XA) 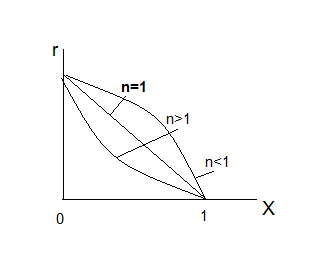 Т.к. 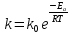 (3) то можно построить концентрационную и конверсионную зависимость r(CA) и r(X) скорости реакции при разных температурах T1 и T2 (T2> T1). (3) то можно построить концентрационную и конверсионную зависимость r(CA) и r(X) скорости реакции при разных температурах T1 и T2 (T2> T1). 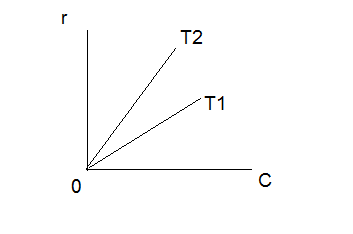 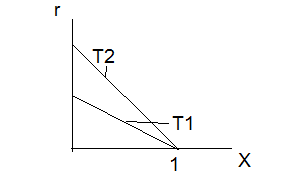 Видно, что при более высокой температуре превращение происходит быстрее. Так как из (3) следует, что увеличением температуры константа скорости реакции возрастает. Таким образом, повышение температуры обуславливает интенсификацию процесса для необратимой реакции. Ограничение температуры вызвано термостойкостью компонентов, появлением нежелательных реакций, возможностью самовоспламенения, устойчивостью материала аппаратуры и т.д. 39. Гомогенный химический процесс: простая обратимая реакция. Обратимая реакция 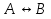 представлена кинетическим уравнением первого порядка в обоих направлениях: представлена кинетическим уравнением первого порядка в обоих направлениях: 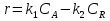 (1) Т.к. скорость реакции зависит от концентрации двух компонентов, зависимость r(CA) представлена рядом кривых, полученных при различных значениях (1) Т.к. скорость реакции зависит от концентрации двух компонентов, зависимость r(CA) представлена рядом кривых, полученных при различных значениях 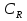 . Точки САР – отвечают состоянию равновесия в реакционной системе, при этом концентрация компонентов равна САР и СRP соответственно. Если СА< САР, скорость реакции отрицательна (штриховая линия). Т.е. реакция протекает в обратном направлении. . Точки САР – отвечают состоянию равновесия в реакционной системе, при этом концентрация компонентов равна САР и СRP соответственно. Если СА< САР, скорость реакции отрицательна (штриховая линия). Т.е. реакция протекает в обратном направлении. 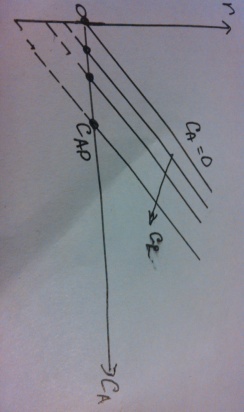 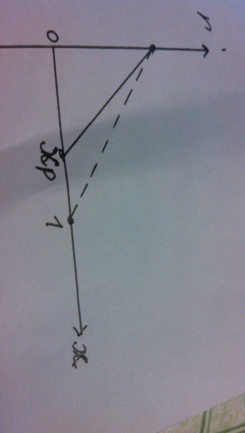 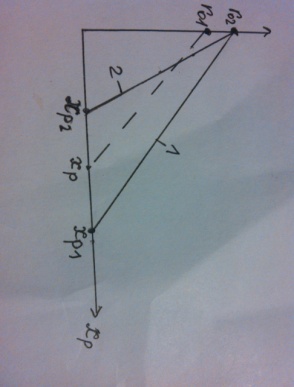 Выразим СА и 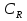 через степень превращения х: через степень превращения х: 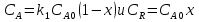 Тогда: 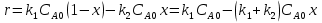 (2) (2)Зависимость r(x) имеет линейно убывающий вид (штриховая линия – зависимость r(x) для необратимой реакции). Из (2) следует, что r=0 при 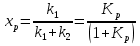 ; КР – константа равновесия; хР – равновесная степень превращения. ; КР – константа равновесия; хР – равновесная степень превращения. 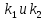 увеличиваются с ростом температуры, но увеличиваются с ростом температуры, но 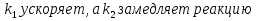 . Их совместное влияние зависит от соотношения энергий активации прямой и обратной реакции. Последнее различно для экзо- и эндотермических реакций. . Их совместное влияние зависит от соотношения энергий активации прямой и обратной реакции. Последнее различно для экзо- и эндотермических реакций.Зависимость r(x) при температуре Т1 (штриховая линия) и при Т2>Т1 (сплошные линии). Если реакцию проводить при более высокой температуре, то начальная (при х=0) скорость увеличивается. Далее равновесие изменяется в зависимости от типа реакции: для эндотермической реакции скорость повышается во всем интервале изменения х; в экзотермической реакции скорость повышается лишь до некоторого момента. Т.о. для экзотермической реакции существуют оптимальные температуры для каждой степени превращения, при которой скорость реакции максимальна. Следовательно, уменьшение температуры по мере протекания реакции, приводящее к максимальной интенсивности данного процесса для обратимой экзотермической реакции. Для обратимой эндотермической реакции оптимальная температура равна максимально допустимой. Проведение процесса при максимально допустимой температуре определяет способ интенсификации процесса для обратимой эндотермической реакции. 40. Базисная система стехиометрических уравнений: стехиометрически независимые уравнения; выбор системы стехиометрических уравнений. Стехиометрические уравнения показывают, в каких соотношениях реагенты вступают во взаимодействие. Они имеют вид: где: А,B – исходные вещества; R,S– продукты реакции; - стехиометрические коэффициенты. Химические превращения могут быть описаны одним или несколькими стехиометрическими уравнениями. В случае, когда имеет место несколько стехиометрических уравнений, стехиометрический коэффициент i-го вещества, j-го уравнения, можно обозначить, как и систему уравнений можно представить в виде: , где n – число реагентов, m – число уравнений , – для исходных реагентов, – для продуктов, – для i-го вещества, не входящего в j-ое уравнение. Совокупность стехиометрических уравнений, однозначно и полно описывающих процесс, называют базисной системой стехиометрических уравнений. Так как со стехиометрическими уравнениями можно делать линейные преобразования (складывать уравнения, переносить члены справа налево и наоборот и т.д.), то возникают трудности при определении базисной системы уравнений, например: процесс получения водорода из природного газа можно записать двумя уравнениями: но можно эти уравнения сложить и тогда: Для расчета данного процесса не достаточно последнего уравнения, хотя оно и является суммой предыдущих. Таким образом, базисная система линейно-независимых стехиометрических уравнений, однозначно описывающих процесс, должна включать все участвующие в химическом превращение вещества и не должна включать ни одного уравнения, которое может быть получено линейными преобразованиями других. В большинстве случаев необходимое число стехиометрических уравнений можно определить по формуле: У=В-Э, где У - число независимых уравнений, В - число веществ (реагентов), Э- число химических элементов из которых состоят реагенты. Так для конверсии метана В=5 ; Э=2 , откуда У=2. Базисная система включает два уравнения. Для отдельных обменных процессов формула имеет вид: У=В-Э+1. 41. Гомогенный химический процесс: сложная реакция, параллельная схема превращения. Параллельную схему превращения можно представить в следующем виде: 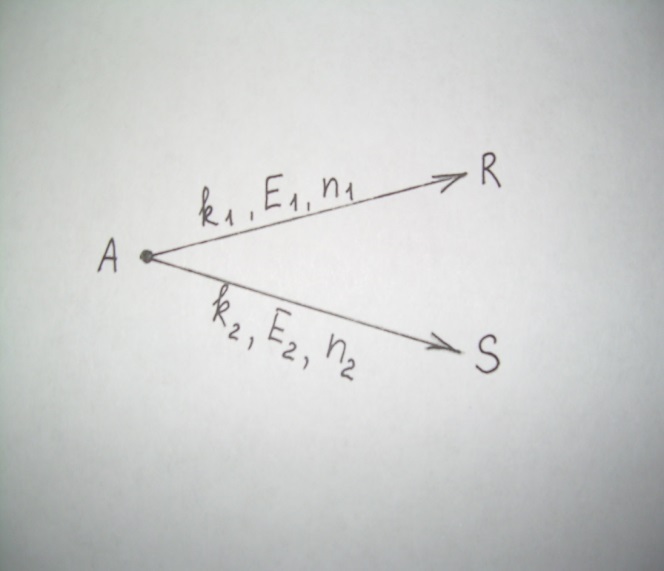 Здесь k1 и k2 – константы скоростей; Е1 и Е2 – энергии активации; n1 и n2 – порядки частных реакций; А – исходное вещество; R и S – основной и побочный продукт. Дифференциальная селективность SR’ по Rопределяется по уравнению: 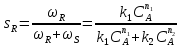 где 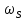 и и 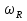 – скорости образования продуктов S и R. – скорости образования продуктов S и R.Если порядок частных реакций одинаков (n1 = n2), то SR’ = 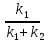 и SR’ (дифференциальная селективность) не зависит от концентрации А. и SR’ (дифференциальная селективность) не зависит от концентрации А. Если n1 > n2, то 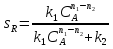 , то есть с ростом СА SR’ возрастает, асимптотически приближаясь к SR’ = 1. , то есть с ростом СА SR’ возрастает, асимптотически приближаясь к SR’ = 1. Если n1 < n2, то 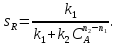 То есть SR’ уменьшается с увеличением СА, асимптотически приближаясь к нулю. То есть SR’ уменьшается с увеличением СА, асимптотически приближаясь к нулю.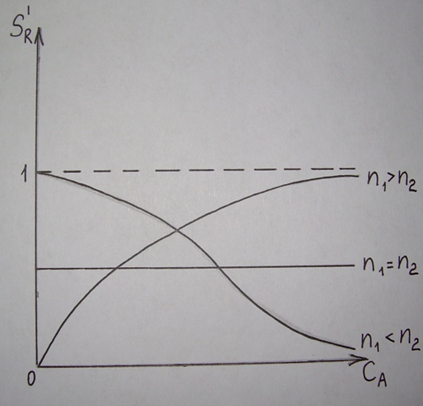 Рис. 1. Зависимость дифференциальной селективности SR’ от концентрации исходного компонента СА для параллельной схемы превращения (n1,n2 – порядок реакций) Из полученных данных можно сделать следующие выводы о целесообразном режиме проведения процесса с параллельной схемой превращения: 1) Если порядок реакции образования целевого продукта больше, чем порядки реакций образования других продуктов, процесс выгоднее проводить при высоких концентрациях исходных веществ тогда и селективность и интенсивность процесса будут наибольшими. 2) При равных порядках частных реакций концентрация не влияет на селективность и повышение концентрации целесообразно для увеличения скорости реакции. 3) Если порядок реакции образования побочного продукта больше, то селективность реакции будет увеличиваться при снижении концентрации исходного вещества. Однако скорость превращения будет уменьшаться. 4) Повышение температуры приведет к увеличению дифференциальной селективности, если при этом скорость образования R возрастет больше, чем скорость образования S. 42. Гомогенный химический процесс: сложная реакция, последовательная схема превращения. Последовательная схема превращения представлена двумя частными этапами: A k1; E1 R k2 ;E2 S 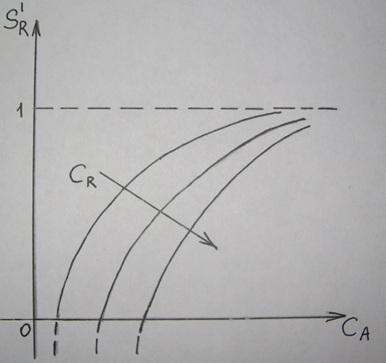 Рис. 2. Зависимость дифференциальной селективности SR’ от концентрации исходного СА и промежуточного CR веществ для последовательной схемы превращения (стрелкой показано увеличение CR). Как видно из рис. 2 увеличение CR при неизменном значении СА приводит к уменьшению SR’, т.к. скорость расходования R возрастает, а скорость его образования не меняется. При некотором соотношении CRи СА , а именно 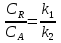 скорости образования Rиз A и дальнейшего превращенияR в Sбудут равны и SR’=0. скорости образования Rиз A и дальнейшего превращенияR в Sбудут равны и SR’=0.Если отношение 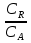 станет больше станет больше 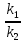 , то SR’станет отрицательной. , то SR’станет отрицательной.Из полученных данных можно сделать следующие выводы о целесообразном режиме проведения процесса с последовательной схемой превращения: 1) Высокую селективность процесса по промежуточному веществу Rможно получить при большой концентрации исходного вещества А и малом содержании промежуточного, то есть при небольшом превращении А, когда Rне накапливается и не претерпевает значительного дальнейшего изменения. 2) Температура будет благоприятно сказываться на селективности, если с ростом температуры k1 увеличивается сильнее, чем k2 . 43. Общие положения. В общем случае в гетерогенном химическом процессе исходные вещества и продукты находятся в разных фазах. По виду участвующих в процессе фаз различают следующие гетерогенные системы: а) «газ-твердое» к этому виду процессов относят адсорбцию и десорбцию газов, обжиг руд, окисление металлов, восстановление твёрдых оксидов, горение твёрдых топлив; б) «жидкость-твердое» - адсорбция, растворение, выщелачивание, экстракция, кристаллизация; в) «газ-жидкость» - абсорбция, конденсация, перегонка жидких смесей, дистиляция,ректификация; г) несмешивающаяся система «жидкость-жидкость» - жидкостная экстракция; д) «твердое-твердое» - спекание, получение цемента, керамики, высокотемпературный синтез неорганических металлов; е) многофазные системы – «газ-жидкость-твердое», «жидкость-жидкость(несмывающаяся) –газ» и т.п. Предметом дальнейшего рассмотрения будут происходящие в этих системах химические превращения. Условия гетерогенного процесса - состояние каждой из фаз и параметры их взаимодействия. Реагенты переносятся к месту протекания реакции, где условия (условия реакции) отличаются от созданных извне. Скорость превращения вещества определяется условиями реакции, которые являются результатом перераспределения концентраций и температур из-за одновременного протекания химической реакции и явлений переноса. Зависимость скорости превращения от условий гетерогенного процесса называю наблюдаемой скоростью превращения WН. Наблюдаемая скорость превращения зависит от условий взаимодействия фаз ( скорости направления потоков, конфигурации поверхности) и их транспортных свойств( диффузия, теплопроводность, вязкость). Во многостадийном процессе интенсивность его составляющих (этапов, стадий) может быть различна. В этой связи вводят понятия лимитирующая стадия ограничивающая скорость процесса (т.е. самая медленная стадия), и режим процесса, определяемый этой стадией, которые будут определенны далее. Механизмы переноса в твердом теле существенно отличаются от таковых в жидкости и газе. Газ и жидкость - фазы текучие с подвижной поверхностью. Вклад конвективной составляющей переноса в них весьма велик, чего нет в твёрдом теле с жесткой и неподвижной внутренней структурой и внешней конфигурацией. Это позволяет для построения моделей химического процесса указанное выше многообразие гетерогенных систем свести к двум видам: «газ (жидкость) -твердое» взаимодействие текучей и жесткой фаз; «газ (жидкость) -жидкость»-взаимодействие текучих фаз. 44. Гетерогенный химический процесс:Система"газ(жидкость)-твердое(полностью реагирующее)" В рассматриваемой системе твердый реагент- кусковой или зернистый материал омыляется потоком жидкого иди газообразного реагента(при построении модели это различие не принципиально, поэтому будем рассматривать систему «газ- твёрдое»). Продукты реакции переходят в газовую фазу. Твердая частица уменьшается. Процесс можно представить уравнением: Ar+BT=Rr (1) Индексы «r » и «T» указывают в какой фазе находятся реагент. Для исследования основных свойств процесса представим твёрдый реагент в виде частица шарообразной формы (см.рисунок1). Предположим ,что температуры частицы и потока равны, а перенос компонентов между потоком и частицей одинаков по всей поверхности частицы (т.е. поверхность частицы- равнодоступная). Примеры таких процессов: горение угля C+O2=CO2 , газификация угля C+H2O=CO2+H2 ,растворение твёрдого вещества. В них происходит уменьшение размеров частиц твёрдого материала по мере протекания процесса вплоть до его исчезновения. 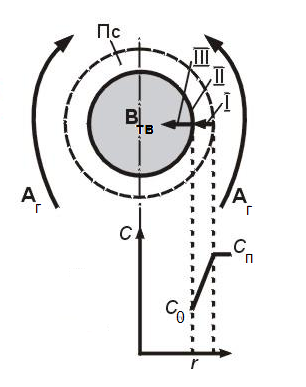 Схема процесса представлена на рис. 1. Рис.1 Схема гетерогенного процесса «сжимающаяся сфера». Sr-поверхность частицы BT с радиусом r. Обтекающий твердую частицу BT поток хорошо перемешан в объеме, так что концентрация газообразного компонента Ar в нем (говорят «в ядре потока») постоянна и равна С0. У поверхностей частицы образуется пограничный слой Пс (на рис. Обозначен штриховой линией). Через него компонент Ar проникает к поверхности частицы, где и происходит реакция. Газообразные продукты Rr удаляются в поток обратным путем. Массообмен между фазами осуществляется с помощью диффузии и характеризуется коэффициентом массообмена: β= 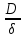 , где D-коэффициент диффузии; , где D-коэффициент диффузии;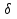 -толщина пограничного слоя. -толщина пограничного слоя.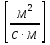 = =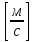 Для расчета коэффициента массообмена 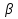 ,который служит описательной характеристикой и для более сложных механизмов переноса, используют критериальные уравнения теории подобия.(см лк 5) ,который служит описательной характеристикой и для более сложных механизмов переноса, используют критериальные уравнения теории подобия.(см лк 5)Структура переноса представлена следующими стадиями(этапами). В газовой фазе:
Для этого концентрация показана в нижней части рис.1
Полагаем, что скорость реакции не зависит от концентрации Rr и его отвод от поверхности не влияет на процесс. В твердой фазе:
Первоначально частица имеет радиус R0 . Такой гетерогенный процесс, где частица твердого реагента уменьшается в размере, называют « сжимающаяся сфера» . Математическая модель описывает поведение взаимодействующих газообразного Ar и твердого BT реагентов. Объемное содержание вещества в твердой частицы в сотни раз больше, чем в газе, и уменьшение размера частицы происходит намного медленнее установления распределения концентраций в пограничном слое, поэтому процессы, протекающие в газовой фазе, можно считать стационарными относительно процесса в твердой фазе. Рассмотрим математические модели процессов протекающих в газовой и твердой фазах. Газообразный реагент. В стационарном режиме поток WI вещества Ar к поверхности (этап I) и скорость WII реагирования Ar на ней (этап II) равны: WI=WII (2) Поток компонента Ar зависит от поверхности Sr частицы с радиусом r и разности концентрации Ar в потоке-С0 и у поверхности Cn: WI= - βSr(c0-cn) 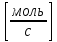 (3) здесь β – коэффициент массообмена, (3) здесь β – коэффициент массообмена, 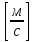 β= 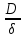 см. рис.1 Пусть на поверхности протекает реакция первого порядка, при этом скорость превращения Ar пропорциональна наружной поверхности частицы Sr : см. рис.1 Пусть на поверхности протекает реакция первого порядка, при этом скорость превращения Ar пропорциональна наружной поверхности частицы Sr :WII= -kcnSr (4) Подставляем (4) и(3) в(2) получим: β(c0-cn)= kcn (5) Далее определим концентрацию Ar у поверхности: Cn= 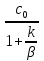 (6) И наблюдаемую скорость превращения: WH= -kcn= - (6) И наблюдаемую скорость превращения: WH= -kcn= - 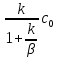 (7) (7)Комбинацию параметров k и β в выражении (7) обозначаем как КH –наблюдаемую константу скорости: КH= 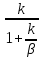 (8) Таким образом подставляя (8) в (7) получаем: (8) Таким образом подставляя (8) в (7) получаем:WH= - KH C0 (9) Полученная кинетическая зависимость, характерна для реакции первого порядка. Однако, если реакция будет иметь другой порядок выражения для наблюдаемой скорости превращения будут отличаться. Твердый реагент. Изменение количества твердого компонента NB [моль] в единицу времени равно скорости его превращения WB протекающего на наружной поверхности частицы Sr : 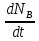 = WB Sr (10) В рассмотренной реакции (1) Ar+BT=Rr , = WB Sr (10) В рассмотренной реакции (1) Ar+BT=Rr , 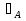 = =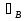 и следовательно скорости превращения веществ одинаковы, т.е. WA=WB т.к и следовательно скорости превращения веществ одинаковы, т.е. WA=WB т.к r = 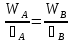 , где r – скорость реакции (1). Таким образом с учетом (4) и (9) можно записать: WB= - KH C0 Sr , где r – скорость реакции (1). Таким образом с учетом (4) и (9) можно записать: WB= - KH C0 Sr Обозначим n0 [моль/м3] количество твердого реагента в единице объема. Если частица непористое вещество плотностью γ [кг/м3] и молярной массой : μ то n0= 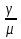 . За время dt прореагирует тонкий поверхностный слой толщины dr, содержащий реагента BT в количестве: dNB=n0 Sr dr. Sr-поверхность частицы BT радиусом r. С учетом сказанного уравнение (10) преобразуем к виду: . За время dt прореагирует тонкий поверхностный слой толщины dr, содержащий реагента BT в количестве: dNB=n0 Sr dr. Sr-поверхность частицы BT радиусом r. С учетом сказанного уравнение (10) преобразуем к виду: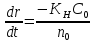 (11) (11)Интегрируя (11) в пределах от начального момента t=0 (первоначальный размер частицы R0) до момента t (размер частицы уменьшился до r ) получим: R0 – r = KH 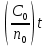 (12) (12)Через какое-то время tK твердая частица прореагирует полностью, то есть в этот момент r = 0, то есть R0 = KH 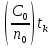 . .Отсюда время полного превращения tK: TK = 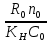 (13) (13)Введя безразмерный радиус ρ = 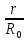 и используя (13) уравнение (12)можно привести к безразмерному виду: Ρ = 1- и используя (13) уравнение (12)можно привести к безразмерному виду: Ρ = 1-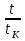 (14) (14)На практике превращение удобно выразить через степень превращения твердого компонента xB = 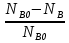 , количество которого в первоначальный момент NB0= , количество которого в первоначальный момент NB0=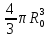 n0 , а в текущий момент NB0 = n0 , а в текущий момент NB0 =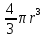 n0 . n0 .Отсюда получаем: xB=1- 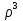 и => и => 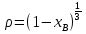 (15) (15)Таким образом изменение степени превращения со временем ,с учетом (14): xB = 1- 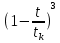 (16) (16)Влияние условий процесса на скорость превращения.
Нагрев на 10 0 увеличивает скорость реакции в два-четыре раза, а диффузию на 2-3%. Поэтому принимают, что k- зависит от температуры, а β – нет .(Для относительно низких температур.)
При малых скоростях потока режим диффузионный и массообмен увеличивается со скоростью потока. При больших скоростях потока режим процесса переходит в кинетический и перестает зависеть от этого параметра. Интенсификация процесса. Используя уравнение (13) TK = 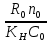 и (8) КH= и (8) КH=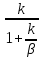 можно получить выражение для времени полного превращения твердого реагента tK : tK = ( можно получить выражение для времени полного превращения твердого реагента tK : tK = (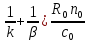 (17) (17)Интенсификацию процесса определяют по уменьшению tK , которое можно достичь:
Влияние температуры и скорости потока на наблюдаемую скорость превращения ограничено соответствующим режимам процесса- кинематическим и диффузионным. |
