ШПОРЫ ОХТ. Цели и задачи курса Общая химическая технология Объект изучения курса
 Скачать 3.94 Mb. Скачать 3.94 Mb.
|
|
63. изотермический процесс в химическом реакторе. Режим идеального смешения периодический и идеального вытеснения. Сложная реакция с параллельной схемой превращения. Математическая модель процессов. 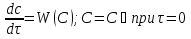 (1) (1)Схема реакции первого порядка 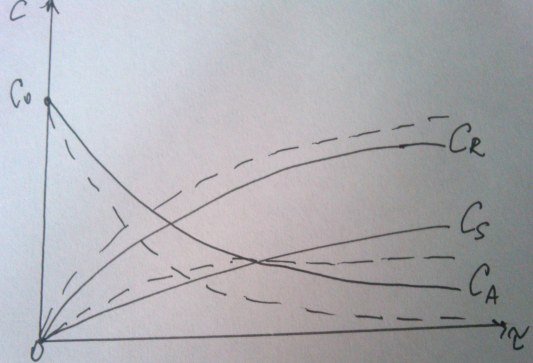 Е1 R А Е2 S Скорости превращения компонентов A, R, S равны 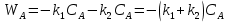 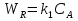 (2) (2)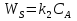 Математический процесс описывается уравнениями: 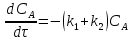 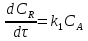 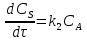 CA=C0; CR=CS=0 при 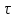 =0 (3) =0 (3)Решение первого уравнения системы (3): 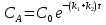 (4) (4)Подставим (4) во второе уравнение системы (3): 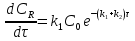 и проинтегрируем: и проинтегрируем: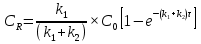 (5) (5)Выражение для CS получим аналогично: 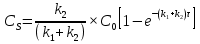 (6) (6)Зависимости концентраций реагентов от 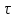 представлены на рисунке:Изменение концентрации реагентов в реакторе ИВ или ИС-п при протекании сложной параллельной реакции. Сплошные линии построены при температуре I1;штриховыепри I2>I1 и E1>E2(E1-энергия активации 1 реакции,Е2-второй). представлены на рисунке:Изменение концентрации реагентов в реакторе ИВ или ИС-п при протекании сложной параллельной реакции. Сплошные линии построены при температуре I1;штриховыепри I2>I1 и E1>E2(E1-энергия активации 1 реакции,Е2-второй).Как видно из рисунка с течением реакции концентрации монотонно изменяются: исходного вещества СА-уменьшается,а продуктов CR и CS – растут 64. Изотермический процесс в химическом реакторе. Режим идеального смешения, периодического и идеального вытеснения. Сложная реакция с последовательной схемой превращения. 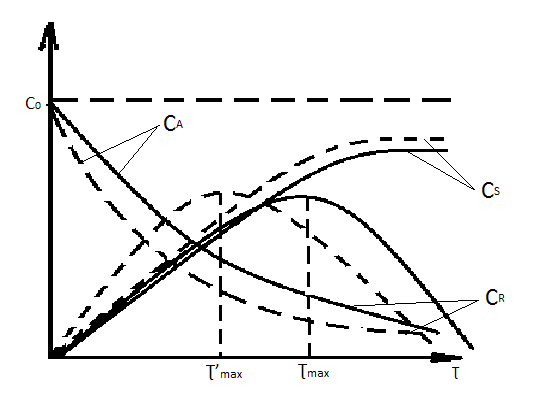 Математическая модель процессов: 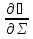 = W(C); С=С0 при = W(C); С=С0 при 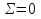 (1) (1)Схема реакции: 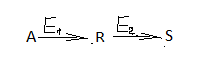 Процесс описывается системой уравнений (для реакций первого порядка): ∂СА/∂Ʈ=-k1CA; (2) ∂CR/∂Ʈ= k1CA-k2CR; ∂СS/∂Ʈ=k2CR; СА=С0; СR=CS=0 при Ʈ=0. Решением первого уравнения является: СA=C0e-k1Ʈ; (3) Подставив его во второе уравнение системы (2) получим: ∂CR/∂Ʈ=k1C0e-k1Ʈ- k2CR; (4) Решением (3) с учетом СR=0 при Ʈ=0 является: CR= 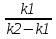 C0[e-k1Ʈ- e-k2Ʈ]; (5) C0[e-k1Ʈ- e-k2Ʈ]; (5) Подставляя (4) в третье уравнение системы (1) находим: CS= С0[1- (k2e-k1Ʈ- k1e-k2Ʈ)/(k2-k1)] (6) График зависимостей (3), (5), (6) представлен на рисунке: Изменение концентрации расчетов в реакторе ИВ или ИС-n при последовательном протекании реакции. Сплошные линии построены при температуре Т1 и энергии активации Е1, штриховые при Т2>Т1 и Е1>Е2. Как видно из рисунка расход в процессе компонента А приводит к уменьшению его концентрации СА. Изменение СR в ходе реакции различно: сначала она возрастает, отражая первый этап схемы А→R→S, затем СА уменьшается, вызывая замедление скорости образования R. Одновременно накопление R усиливает его дальнейшее превращение в S. В какой-то момент (Ʈmax) скорости образования и расходования R сравниваются и далее R расходуется на образование S, чему соответствует уменьшение СR. Таким образом в кинетике процесса выделяют следующие этапы: в начале превращения скорость образования S небольшая из-за малого содержания R. Затем при накоплении определенного количества R, интенсивность образования S возрастает и в конце реакции остается один конечный продукт S. Таким образом интегральная селективность по промежуточному продукту R уменьшается с глубиной превращения. 67. Изотермический процесс в химическом реакторе. Режим идеального смешения в проточном реакторе. Сложные реакции. Здесь рассмотрим только описание процесса и решение уравнение модели для частных реакции первого порядка. Параллельная схема превращения: А 1 R 2 S Модель: (cA – c0)/ τ = -(k1+k2)cA cR / τ = k1cA cS / τ = k2cA Решение: cA = c0 / [1+( k1+k2)τ] cR = k1τc0/ [1+( k1+k2)τ] cS = k2τc0/ [1+( k1+k2)τ] Последовательная схема превращения: A 1 R 2 S Модель: (cA – c0)/ τ =-k1cA cR / τ = k1cA- k2 cR cS / τ = k2 cR Решение: cA = c0 /(1+k1τ) cR = k1τc0/ [(1+k1τ)( 1+k2τ)] cS = k1k2τ2c0/ [(1+k1τ)( 1+k2τ)] Качественный характер зависимостей c(τ), влияние на них температуры, а также изменение селективности c(τ) [SR (τ)] будут такими же, как и в режимах идеального вытеснения 65. Изометрический процесс в химическом реакторе. Режим идеального смешения в проточном реакторе. Простая необратимая реакция A=R. Математическая модель процесса: 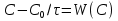 (1) (1)Скорость превращения для реакции первого порядка: W(C) = -kC; отсюда (1) принимает вид: 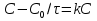 (2) (2)Или, переходя к степеням превращения 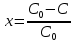 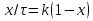 (3) (3)Решением (2) и (3) является 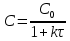 и и 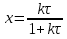 (4) (4)Зависимость С( 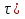 показана на рисунке: показана на рисунке: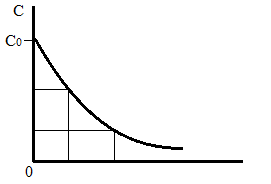 ��1 ��2 �� Аналитическое решение уравнения (2) относительно С для реакции не первого порядка(кроме n=0,5 и n=2) ограничено. Удобнее определять необходимое время реакции для достижения заданной концентрации С из (1): 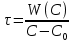 . .Интерпретация полученного решения Для каждого конкретного проточного реактора UC-H условное время 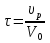 - фиксированная величина . ( - фиксированная величина . (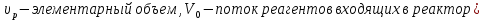 Зависимость С(��) , показанная на рисунке есть геометрическое место точек, соответствующих достижению заданных С при �� характерных для различных реакторов. То есть кривая есть графическое отображение функции (4) , и зависимость С(��) есть набор режимов различных реакторов, но не изменение концентрации в одном из них, как это имеет место в реакторах UB и UC-n. Концентрация вещества в режиме UC-Hодинакова во всех точках реактора и равна С, на входе - С0 .Это означает, что на входе происходит скачок концентрации от С0 до С. Т.о. распределение концентраций в координатах «С-��» является ступенчатой линией «Высота ступени», равная (С0 -С) , для каждого реактора индивидуальна. На рисунке такие зависимости даны при различных значениях �� , то есть или для реакторов разного объема 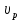 , или для одного реактора, работающего при разных нагрузках V0 на него. , или для одного реактора, работающего при разных нагрузках V0 на него.66. Изотермический процесс в химическом реакторе. Режим идеального смещения в проточном реакторе. Простая обратимая реакция А↔R. (C-C0)/τ = W(C) Математическая модель процесса: (1) X/τ = k1(1-X)−k2X Модель процесса (1), в которой концентрация компонентов выражена через степень превращения X(CA=C0(1-X) и СR= C0X) имеет вид: , или (2) X= k1τ/(1+( k1+ k2) τ) (3) Х= k1/( k1+ k2) Предельное значение Х при τ→∞: , (4) Что соответствует равновесной степени превращения. Зависимость Х(τ) имеет вид: рассматриваемая реакция имеет первый порядок в прямом и обратном направлениях, поэтому начальная концентрация С0 не влияет на степень превращения. 68. Неизотермический процесс в химическом реакторе. Организация теплообмена в реакторе и температурные режимы. Химическое превращение связано с изменением энтальпии реагирующей смеси, выделением или поглощением теплоты. Это изменяет температуру процесса и значит влияет на скорость химического превращения. В ходе процесса возможен обмен теплотой с теплоносителем, что позволяет создавать желаемые температурные условия протекания реакции. Рассмотрим варианты организации тепловых потоков.
Теплота, потребляемая эндотермической реакцией, поступает с исходным веществом, а продукт выходит охлажденным. В реакторах, близких к режиму идеального вытеснения (ИВ), температура реакционной смеси меняется по мере ее продвижения и процесс в реакционной зоне – неизотермический. В реакторах близких к режиму идеального смешения (ИС) процесс в реакционной зоне протекает изотермически, хотя в целом процесс считается адиабатическим. Т.к. выделяемая или затрачиваемая теплота реакции расходуется только на нагрев или охлаждение реакционной смеси.
Теплообмен может осуществляться через поверхность ограничивающую место протекания реакции, как это организованно в емкостном аппарате или в трубчатых реакторах. Теплообменник может быть встроен в реакционную зону, как в реакторе типа печь. Смесь реагентов может циркулировать через выносной теплообменник. Это обеспечивает теплообмен непосредственно в реакционной зоне. Другой способ отвода тепла из зоны реакции является испарение части реакционной смеси в процессе протекания реакции. Образующиеся пары конденсируют для возврата в реактор, что делает схему теплообмена аналогичной с выносным теплообменником. Возможен отвод тепла только за счет испарения жидкости, обычно растворителя(напр при барботаже). Изменяя давление в реакторе изменяют содержание уносимых паров в газовом потоке и тем самым количество теплоты, отводимой с ним. Температурный режим в таких реакторах может быть изотермическим ( а аппаратах с интенсивным перемешиванием) или с переменной температурой ( в трубчатых реакторах). В многослойных реакторах или в последовательности реакторов теплообмен осуществляется с помощью поверхностных теплообменников, расположенных вне реакционной зоны, а так же вводом холодной или горячей реакционной смеси или ее компонентов в сам реактор. 69. Неизотермический процесс в химическом реакторе. Режимы идеально смешивания периодического и идеального вытеснения. Анализ процесса. Математическая модель процесса 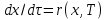 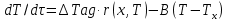 (1) (1)при τ=0 x=xн; T=Tн где 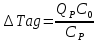 – адиабатический разогрев; – адиабатический разогрев; 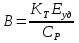 – параметр теплоотвода; Tx – температура теплоносителя, xниTн соответственно начальная степень превращения и температура на входе в реактор; – параметр теплоотвода; Tx – температура теплоносителя, xниTн соответственно начальная степень превращения и температура на входе в реактор; x=(C0-C)/C0. Аналитического решения (1) в общем случае нет. В адиабатическом режиме B=0 => система (1) принимает вид: 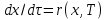 (2) (2) 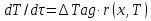 ; при τ=0 x=xн; T=Tн ; при τ=0 x=xн; T=TнРазделим второе уравнение системы (2) на первое 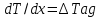 проинтегрируем его в пределах от xн до x и от Tндо T получим: T-Tн= проинтегрируем его в пределах от xн до x и от Tндо T получим: T-Tн=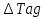 (x-xн) (3) (x-xн) (3)Где (T-Tн) – разогрев реакционной смеси до достижения степени превращения x. Если xн = 0, а реакция будет проведена до концы (х=1), то реакционная смесь нагреется на T-Tн= 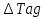 - на величину адиабатического разогрева. Анализируя уравнение 3 делаем вывод, что результат процесса (конечная температура I) зависит от изменения состояния химически реагирующей системы (степени превращения х) и не зависит от пути превращения, от кинетики. Зависимость степени превращения х от темперетуры I для адиабатического процесса в режиме UB дана на рисунке: - на величину адиабатического разогрева. Анализируя уравнение 3 делаем вывод, что результат процесса (конечная температура I) зависит от изменения состояния химически реагирующей системы (степени превращения х) и не зависит от пути превращения, от кинетики. Зависимость степени превращения х от темперетуры I для адиабатического процесса в режиме UB дана на рисунке:1 – эндотермическая реакция 2, 2' – экзотермическая реакция (сплошная линия соответствует ∆Tag, штриховая - ∆Tag'>∆Tag 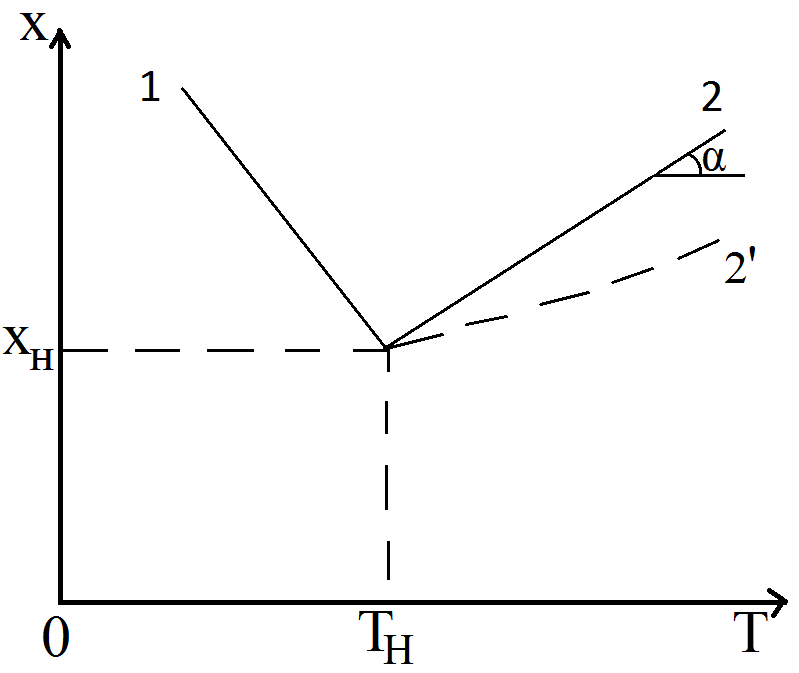 Зависимость x(T) адиабатического процесса представляет прямую линию с tgα, равным обратной величине адиабатического разогрева: 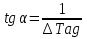 (см (3)), причем для экзотермической реакции наклон положительный (QP>0 и ∆Tag>0), а для эндотермической отрицательный (∆QP<0 и ∆Tag<0). (см (3)), причем для экзотермической реакции наклон положительный (QP>0 и ∆Tag>0), а для эндотермической отрицательный (∆QP<0 и ∆Tag<0).Чем больше адиабатический разогрев ∆Tag, тем более пологий наклон приобретает зависимость x(T) , то есть реакционная смесь будет сильнее разогреваться или охлаждаться. Протекание реакции сопровождается ростом степени превращения x и увеличением (экзотермическая реакция) или уменьшением (эндотермическая реакция) температуры T. Максимальный разогрев достигается при x=1 и xн=0 и равен ∆Tag На процесс влияет исходная концентрация, увеличение которой приводит к повышению ∆Tag, и следовательно к ускорению превращения. 70. Неизотермический процесс в химическом реакторе. Режимы идеального смешения периодический и идеального вытеснения с теплообменом. Сопоставление адиабатического процесса и изотермическим. Допустим, изотермический процесс осуществляется при температуре адиабатического экзотермического процесса и превышающую ее в эндотермическом процессе. 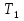 = . = . 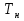 (. (. 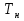 - температура на входе в реактор). В первом случае изотермический процесс будет менее интенсивным, чем адиабатический, а во втором большая степень превращения будет достигаться при меньшем времени реакции. - температура на входе в реактор). В первом случае изотермический процесс будет менее интенсивным, чем адиабатический, а во втором большая степень превращения будет достигаться при меньшем времени реакции.Если же температура изотермического процесса . 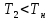 то интенсивность изотермического процесса будет выше, чем адиабатического, и это будет наблюдаться до тех пор, пока возрастающая в течение реакции температура не достигнет . то интенсивность изотермического процесса будет выше, чем адиабатического, и это будет наблюдаться до тех пор, пока возрастающая в течение реакции температура не достигнет . 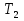 (для экзотермической реакции) (для экзотермической реакции)В эндотермическом процессе при 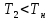 картина будет обратной. Если реакция обратимая, то общий характер зависимости степени превращения Х и температуры Т от картина будет обратной. Если реакция обратимая, то общий характер зависимости степени превращения Х и температуры Т от 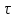 (условного времени реакции сохраняется, с отличием лишь в том, что процесс будет протекать только до равновесной степени превращения (условного времени реакции сохраняется, с отличием лишь в том, что процесс будет протекать только до равновесной степени превращения 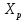 . Тогда максимальный разогрев будет: . Тогда максимальный разогрев будет: Т- 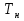 = = 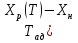 ] (4) ] (4)Значения максимального разогрева определяют из графика «Т-Х» 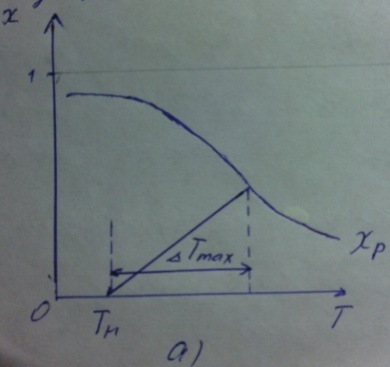 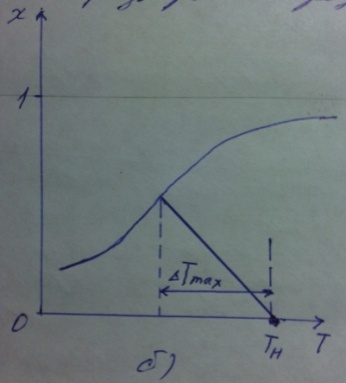 Зависимость 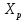 и и 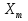 для адиабатического процесса. для адиабатического процесса. Определение максимального адиабатического разогрева  при протекании обратимых а)экзотермической и б) эндотермической реакции при протекании обратимых а)экзотермической и б) эндотермической реакции 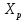 - равновесные степени превращения; прямые – адиабаты в режиме ИВ. - равновесные степени превращения; прямые – адиабаты в режиме ИВ.Пересечение кривых зависимостей 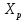 (Т) и Х(Т) адиабатического процесса соответствует максимальному нагреву в слое - (Т) и Х(Т) адиабатического процесса соответствует максимальному нагреву в слое - 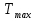 как показано на рисунке а) и б). Интерпритация результатов исследования модели на реальный объект. как показано на рисунке а) и б). Интерпритация результатов исследования модели на реальный объект.Исследованная модель описывает процесс в реакторах ИВ и идеального смешения периодическом ИС-п. В первом случае зависимости Х ( 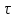 ) и Т( ) и Т( 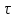 ) (степени превращения и температуры от условного времени реакции) описывают изменение Х и Т по длине реактора, не меняющегося во времени протекания реакции. ) (степени превращения и температуры от условного времени реакции) описывают изменение Х и Т по длине реактора, не меняющегося во времени протекания реакции.Во – втором изменение во времени Х и Т распределение которых по объему реактора в каждый момент времени одинаковы. |
