ШПОРЫ ОХТ. Цели и задачи курса Общая химическая технология Объект изучения курса
 Скачать 3.94 Mb. Скачать 3.94 Mb.
|
|
57. Математическая модель процессов в реакторах типа емкостной проточный реактор, реактор колонный, реактор с «кипящим» слоем и в реакционной зоне многослойного реактора. Процессы в реакторах типа емкостной проточный реактор, реактор колонный, а также реактор с псевдоожиженным или кипящим слоем ( рис 2,3 и 8 лк N 5) и в реакционной зоне многослойного реактора (рис 11 лк N5) . Схема процесса представлена на рисунке 2: 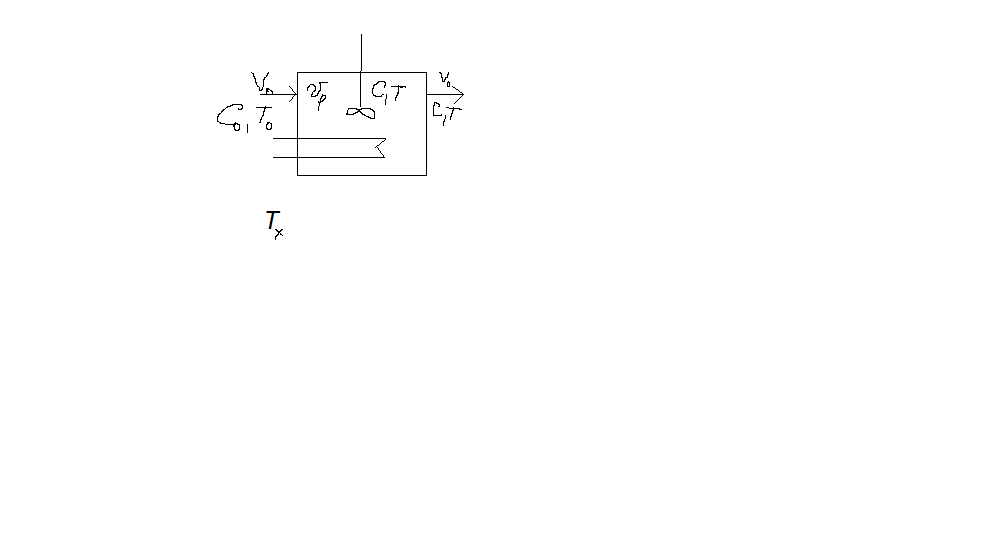 Схема реактора в режиме идеального сложения проточном или непрерывном ( ИС-н). Рассматриваем одну из фаз, интенсивно перемешиваемую. Реактор проточный. Процесс протекает непрерывно в стационарном состоянии (лат. Stationarius – стоящий, неподвижный, то есть не изменяющийся со временем) то есть 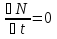 и и 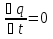 . В единицу времени в реактор входит поток реагентов объёмом . В единицу времени в реактор входит поток реагентов объёмом 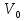 содержащий компоненты в количестве содержащий компоненты в количестве 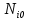 = =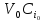 .Температура во входном потоке - .Температура во входном потоке - 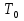 . Принимаем, что объём реакционной смеси не меняется. Из реактора выходит поток объемом . Принимаем, что объём реакционной смеси не меняется. Из реактора выходит поток объемом 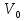 с температурой T и содержанием компонента - с температурой T и содержанием компонента - 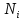 = = 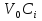 . Очевидно, что концентрации . Очевидно, что концентрации 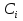 и температура T в выходном потоке такие же, как в реакторе. Источник веществ – химическое превращение, а элементарным объёмом и температура T в выходном потоке такие же, как в реакторе. Источник веществ – химическое превращение, а элементарным объёмом 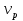 является вся интенсивно перемешиваемая реакционная зона, то есть : является вся интенсивно перемешиваемая реакционная зона, то есть :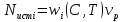 . Уравнение (1) принимает вид: . Уравнение (1) принимает вид:0 = 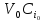 - - 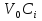 + +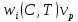 (8) (8)Определим отношение 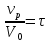 - как условное время реакции, названное так из-за своей размерности: - как условное время реакции, названное так из-за своей размерности: 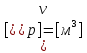 ; ; 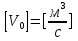 => => 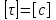 . По виду выражение . По виду выражение 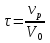 похоже на определение среднего времени пребывания потока в объёме реактора, но обычно похоже на определение среднего времени пребывания потока в объёме реактора, но обычно 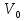 измеряют при нормальных условиях, а температура в реакторе и объём реакционной смеси измеряют при нормальных условиях, а температура в реакторе и объём реакционной смеси 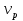 в нем отличаются от нормальных условий. Таким образов уравнение (8) преобразуется: в нем отличаются от нормальных условий. Таким образов уравнение (8) преобразуется: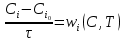 (9)Источник теплоты в реакторе – химическое превращение - (9)Источник теплоты в реакторе – химическое превращение - 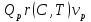 и теплообмен - и теплообмен - 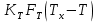 . Полагаем, что теплоемкость . Полагаем, что теплоемкость 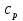 реакционной смеси не меняется в процессе. С учетом этого уравнение (2) будет выглядеть следующим образом: реакционной смеси не меняется в процессе. С учетом этого уравнение (2) будет выглядеть следующим образом: 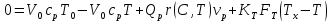 (10) Используя определение условного времени (10) Используя определение условного времени 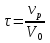 и удельной поверхности теплообмена и удельной поверхности теплообмена 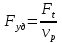 из (10) получаем : из (10) получаем : 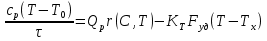 (11) Начальные условия – концентрации (11) Начальные условия – концентрации 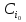 и температура и температура 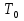 – входят в уравнения (9) и (11). Такой процесс и описывающие его уравнения называют режимом ( моделью) идеального смешения непрерывным ИС-н. – входят в уравнения (9) и (11). Такой процесс и описывающие его уравнения называют режимом ( моделью) идеального смешения непрерывным ИС-н. 58. Математическая модель процессов в реакторах типа насадочный реактор, реактор с неподвижным твердым реагентом, наклонно установленный вращающийся цилиндрический реактор, реактор с просыпающимся навстречу газу твердым реактором, трубчатый реактор, реактор типа печь и многослойный реактор. Процессы в реакторах типа насадочный реактор, реактор с неподвижным твердым реагентом, наклонно установленный вращающийся цилиндрический реактор, реактор с просыпающимся навстречу газу твердым реагентом, трубчатый реактор, реактор типа печь и многослойный реактор протекает непрерывно. 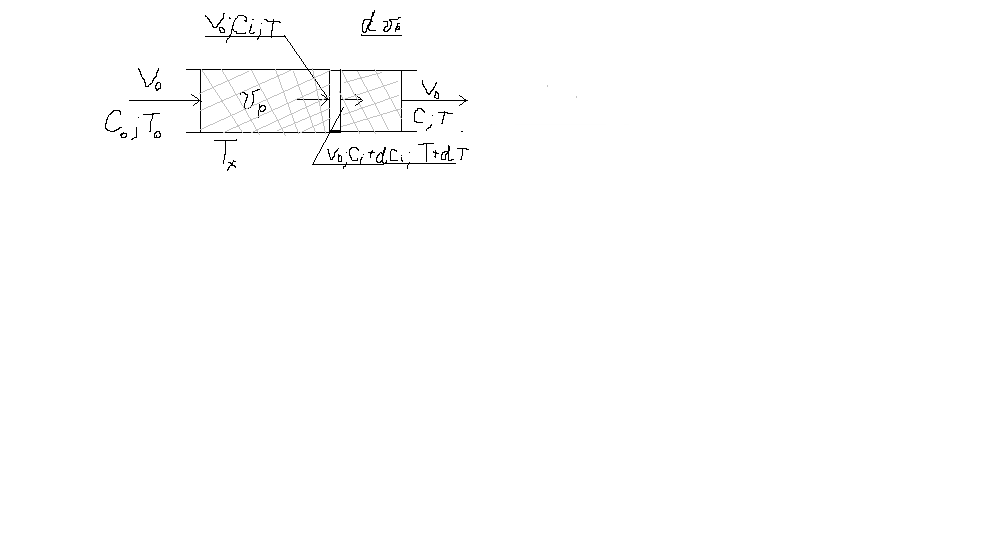 Рассматриваем режим течения потока через реактор без перемешивания. Профиль скорости по сечению потока принимаем плоским. Это возможно допустить , так как во многих реакторах масштаб отклонения во много раз меньше масштаба реакционной зоны. Такой режим потока называют поршневым, или идеального вытеснения. Реактор представим в виде трубки длиной l и сечением S, через который проходит поток реакционной смеси величиной 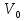 . .Схема реактора идеального вытеснения (ИВ). По мере прохождения реакционной смесью реактора изменяются концентрации компонентов 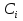 и, в общем случае, температура потока T, вследствие химических превращений. Одновременно с протеканием реакции возможен теплообмен с теплоносителем через стенку. Элементарный объем в этом случае ( выделен на рисунке 3), участок длинной dl и объёмом d и, в общем случае, температура потока T, вследствие химических превращений. Одновременно с протеканием реакции возможен теплообмен с теплоносителем через стенку. Элементарный объем в этом случае ( выделен на рисунке 3), участок длинной dl и объёмом d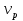 = S * dl. В него потоком входит компонент I в одном количестве: = S * dl. В него потоком входит компонент I в одном количестве: 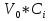 , а выходит в другом: , а выходит в другом: 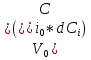 . Источник вещества в выделенном объёме – химическое превращение: . Источник вещества в выделенном объёме – химическое превращение: 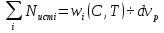 Процесс протекает стационарно ( Процесс протекает стационарно (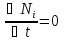 ). Объём реакционной смеси меняется и уравнение (1) принимает вид: ). Объём реакционной смеси меняется и уравнение (1) принимает вид: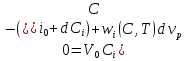 (12) Используя приведенное выше условное время реакции (12) Используя приведенное выше условное время реакции 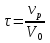 и соответственно, и соответственно, 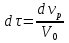 , получим: , получим: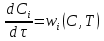 (13) Скорость потока, рассчитанная на все сечение реактора при нормальных условиях (13) Скорость потока, рассчитанная на все сечение реактора при нормальных условиях 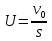 , объем реактора , объем реактора 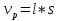 , таким образом условное время потока: , таким образом условное время потока: 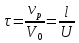 Тепловое уравнение (2) данного процесса: dq/dt=0 – процесс стационарный; Тепловое уравнение (2) данного процесса: dq/dt=0 – процесс стационарный; 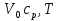 – тепловой поток, входящий в элементарный объем – тепловой поток, входящий в элементарный объем 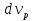 ; ; 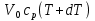 – выходящий поток из него; – выходящий поток из него;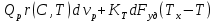 - источник теплоты (т.е. химическое превращение + теплообмен через боковую поверхность 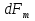 , в выделенном объеме , в выделенном объеме 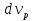 ).Подставляя указанное в (2) получаем: ).Подставляя указанное в (2) получаем: 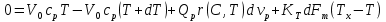 (14) (14)Определим удельную поверхность теплообмена: 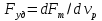 . (Для трубки диаметром . (Для трубки диаметром 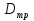 удельная поверхность равняется: удельная поверхность равняется: 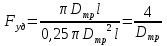 ) Таким образом, с учетом ) Таким образом, с учетом 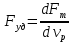 и и 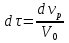 выражение (14) можно записать следующим образом: выражение (14) можно записать следующим образом: 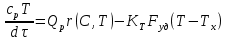 (15) (15)Для замыкания двух дифференциальных уравнений (13) и (15) задают начальные условия: концентрации 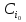 и температура и температура 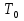 на входе в реактор. на входе в реактор.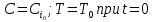 (16) Такой процесс и описывающие его уравнения называют режимом ( моделью) идеального вытеснения – ИВ. (16) Такой процесс и описывающие его уравнения называют режимом ( моделью) идеального вытеснения – ИВ.59. Классификация процессов в химическом реакторе и их математических Моделей.Следует следующая классификация химических реакторов:
1.2.1. Проточный реактор (непрерывный). 1.2.2. Непроточный реактор (периодический). 2. Организация тепловых потоков. 2.1. Температурный режим процесса. 2.1.1. Изотермический. 2.1.2. Неизотермический. 2.2. Тепловой режим реактора. 2.2.1. Адиабатический. 2.2.2. С внешним теплообменом. 62.Изотермический процесс в химическом реакторе. Режим идеального смешения периодического и идеального вытеснения. Простая обратимая реакция А↔ R Математическая модель процессов: dc/d ῖ =W (с);с=с0 ,при ῖ =0 (1) Где ῖ= ῖ ; t в зависимости от процесса. Скорость реакции r(c)=k1cA-k2cB зависит от концентраций сА и сВ, следовательно для описания процесса используют два уравнения вида (1) . Перейдем к одной переменной – степени превращения х реагента А: сА=с0(1-х) и cR=c0x ,где с0-исходная концентрация реагента А. Модель процесс примет вид : dx/dῖ=k1(1-x)-k2x ; х=0 ,при ῖ =0 (2) Преобразуем (2) к виду dx/dῖ=k1 -(k1+k2)x и проинтегрируем его : ln k1-(k1+k2)x-ln k1/k1+k2=ῖ , или х =k1/k1+k2 [1-e-(k1+k2) ῖ ] (3) 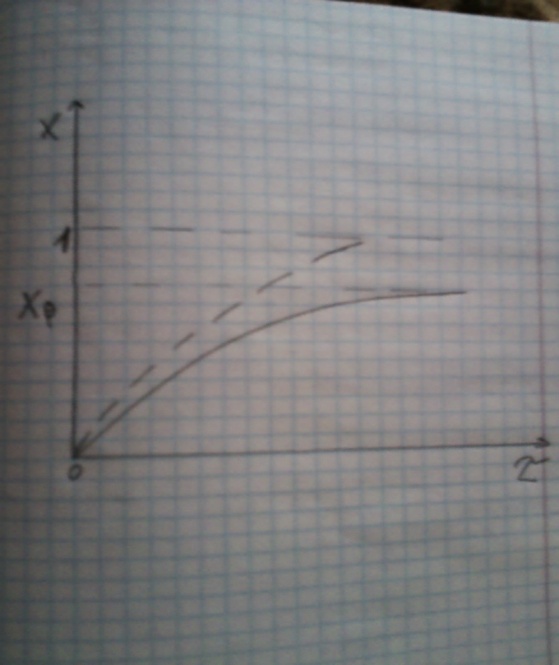 Из (3) видно ,что с увеличением ῖ х(ῖ) увеличивается вплоть до х=k1/k1+k2 при ῖ→∞. Т.к.константа равновесия обратимой реакции Kр=k1/k2 и равновесная степень превращения xр =Kр/1+Kр, то предельное превращение достигаемое в реакторе равно : 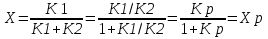 (4) (4)Это естественно ,т.к реакция протекает до равновесия .Зависимость х(ῖ) для простой обратимой реакции (сплошная линия ) и обратимой реакции (штриховая линия ) представлена на рисунке. Рассматриваемая реакция имеет первый порядок в прямом и обратном направлении ,поэтому начальная концентрация с0 не влияет на степень превращения . 60. Анализ процесса в химическом реакторе. Анализ процесса в химическом реакторе исследования влияния условий процесса и характеристик( свойств) его составляющих на показатели работы реактора, а также выявление особенностей процесса и режима. Условия процесса – состав исходной реакционной смеси ( исходные концентрации реагентов 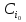 ), объем поступающего потока ( нагрузка на реактор ), объем поступающего потока ( нагрузка на реактор 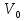 ), температуры входного потока ), температуры входного потока 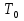 , хладагента , хладагента 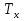 ( для процессов с теплоотводом) или в реакторе ( для процессов с теплоотводом) или в реакторе ( для изотермического процесса – ( для процессов с теплоотводом) или в реакторе ( для процессов с теплоотводом) или в реакторе ( для изотермического процесса – 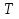 ). ).Режимы процесса – характеристики химического процесса, схема превращения и тип реакций( вид кинетических уравнений), энергия активации, тепловой эффект; для неизотермических процессов – параметры теплоотвода ( коэффициенты теплопередачи 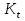 , величина поверхности теплообмена , величина поверхности теплообмена 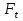 , теплофизические свойства потока , теплофизические свойства потока 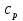 ). ).Показатели процесса – степень превращения x, селективность – S, выход продукта E, а также профили концентраций, степени превращения и температуры в реакторе, их изменение во времени. Зная эти показатели, можно далее определять и другие: конструктивные параметры реактора, энергетические затраты, экономические показатели и др. Особенности процесса и режима – влияние условий и свойств процесса на его показатели, управление процессом ( изменение условий и свойств для достижения желательных показателей); критические режимы ( например, их существование , неустойчивость). Анализ процесса в химическом реакторе осуществляют с использованием методов математического моделирования. Один из вариантов последовательности проводимого анализа рассмотрим ниже.
61. ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС В ХИМИЧЕСКОМ РЕАКТОРЕ. РЕЖИМ ИДЕАЛЬНОГО СМЕШЕНИЯ И ИДЕАЛЬНОГО ВЫТЕСНЕНИЯ. ПРОСТАЯ НЕОБРАТИМАЯ РЕАКЦИЯ А=R. Математическая модель процессов 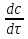 =w (c); c = c0 при =w (c); c = c0 при 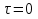 (1) (1) Где 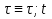 в зависимости от процесса в зависимости от процессаМатематическая модель для реакции первого порядка: (т.к. w(c) = -RC): (2) 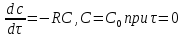 (3) (3)Интегрируя (3) получил: 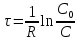 и С и С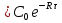 (4) (4) Выражая концентрацию через степень превращения [ 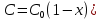 , получим из (3): , получим из (3): 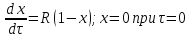 (5) (5)И его решением будет 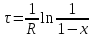 и и 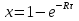 (6) (6)Графики С ( 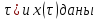 на рисунке на рисунке 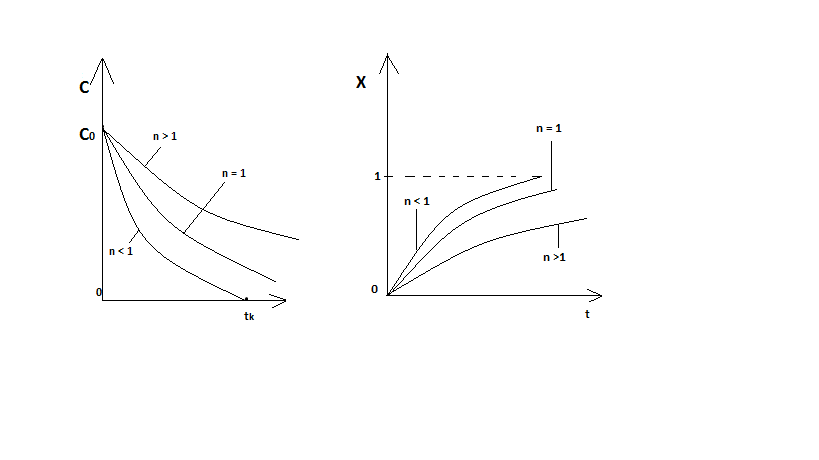 Из графиков видно, что при 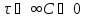 или x или x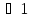 соответственно, следовательно, в необратимой реакции исходное вещество постепенно расходуется до его полного превращения. соответственно, следовательно, в необратимой реакции исходное вещество постепенно расходуется до его полного превращения.Интерпретация решения (4) уравнений математической модели (1) на процессы в режимах ИС - п и ИВ следующая. В режиме ИС – п процесс не стационарен 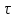 ≡ t и со временем t концентрация исходного вещества C уменьшается в соответствии с (4). ≡ t и со временем t концентрация исходного вещества C уменьшается в соответствии с (4).Но в каждый момент времени – концентрация C во всех точках реактора одинакова. В режиме ИВ процесс протекает стационарно. Концентрация C меняется по длине 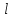 реактора реактора 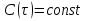 . .То анализ зависимостей С 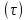 (4) или (4) или 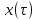 (6) показывает влияние условий процесса на изменение концентрации С, или степени превращения x во времени в режиме ИС – п и распределение C и x по длине реактора в режиме ИВ. (6) показывает влияние условий процесса на изменение концентрации С, или степени превращения x во времени в режиме ИС – п и распределение C и x по длине реактора в режиме ИВ.62.Изотермический процесс в химическом реакторе. Режим идеального смешения периодического и идеального вытеснения. Простая обратимая реакция А↔ R Математическая модель процессов: dc/d ῖ =W (с);с=с0 ,при ῖ =0 (1) Где ῖ= ῖ ; t в зависимости от процесса. Скорость реакции r(c)=k1cA-k2cB зависит от концентраций сА и сВ, следовательно для описания процесса используют два уравнения вида (1) . Перейдем к одной переменной – степени превращения х реагента А: сА=с0(1-х) и cR=c0x ,где с0-исходная концентрация реагента А. Модель процесс примет вид : dx/dῖ=k1(1-x)-k2x ; х=0 ,при ῖ =0 (2) Преобразуем (2) к виду dx/dῖ=k1 -(k1+k2)x и проинтегрируем его : ln k1-(k1+k2)x-ln k1/k1+k2=ῖ , или х =k1/k1+k2 [1-e-(k1+k2) ῖ ] (3)  Из (3) видно ,что с увеличением ῖ х(ῖ) увеличивается вплоть до х=k1/k1+k2 при ῖ→∞. Т.к.константа равновесия обратимой реакции Kр=k1/k2 и равновесная степень превращения xр =Kр/1+Kр, то предельное превращение достигаемое в реакторе равно : 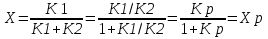 (4) (4)Это естественно ,т.к реакция протекает до равновесия .Зависимость х(ῖ) для простой обратимой реакции (сплошная линия ) и обратимой реакции (штриховая линия ) представлена на рисунке. Рассматриваемая реакция имеет первый порядок в прямом и обратном направлении ,поэтому начальная концентрация с0 не влияет на степень превращения . |
