Цели, задачи и основания проведения экспертизы Специфичные задачи
 Скачать 4.41 Mb. Скачать 4.41 Mb.
|
|
Коэффициент весомости — количественная характеристика степени значимости конкретного показателя для оценки качества. Определение коэффициентов весомости показателей качества проводится экспертным методом. Коэффициенты весомости предназначены для повышения достоверности экспертной оценки качества товаров. Каждый показатель занимает в номенклатуре показателей качества по значимости определенное место. Например, для потребителей многих пищевых продуктов наибольшую значимость имеют вкус и запах, внешний вид, затем консистенция и содержание отдельных веществ. Таким образом, оценивая товар при покупке, потребитель непроизвольно ранжирует показатели по степени их значимости на основании прошлого опыта. Такое ранжирование показателей по степени значимости эксперты осуществляют на основании профессиональных знаний и умений. Кроме того, любой квалифицированный эксперт стремится оценить показатели качества обследованного товара с позиций массового потребителя. Для определения коэффициентов весомости используются шкалы порядка, интервалов и отношений, но наибольшие преимущества перед другими имеет шкала порядка благодаря относительной простоте экспертной оценки показателей качества по степени значимости. Шкала порядка — шкала, предназначенная для упорядочивания (ранжирования) в возрастающем или убывающем порядке количественных характеристик свойств товаров и/или их коэффициентов весомости. При определении коэффициентов весомости показателей качества эксперты сначала оценивают наиболее важный из этих показателей (по их мнению) и присваивают ему определенное число, например 1. Все последующие показатели оцениваются в убывающем или возрастающем порядке по степени значимости. Например, второй по значимости показатель может получить значение 2 (или 0,5) и т. д. После этого данные всех экспертов усредняются по каждому показателю. Наряду со шкалой порядка в практике оценки довольно часто используется метод определения коэффициентов весомости, названный методом фиксированной суммы. Сущность его заключается в том, что эксперты назначают коэффициенты весомости показателей, входящих в показатель верхнего уровня, причем сумма этих коэффициентов должна быть равна заранее определенному числу: 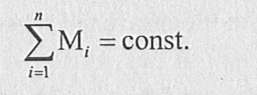 Для корректировки результатов эксперты обычно делят коэффициент весомости каждого показателя на число, равное сумме всех коэффициентов весомости. Кроме того, можно уменьшать или увеличивать коэффициенты весомости отдельных показателей, пока ограничение не будет выполнено. «Метод фиксированной суммы» целесообразно применять только при небольшом количестве сравниваемых показателей. Лимитирующим фактором при использовании этого метода являются трудовые затраты технического работника, а не экспертов. Коэффициенты весомости показателей, составляющих иерархию, назначаются сначала для единичных показателей второго уровня относительно первого, затем третьего относительно второго и т. д. Лишь после этого определяются коэффициенты весомости единичных показателей первого уровня относительно качества в целом. Приведенные выше способы определения коэффициентов весомости с использованием шкал порядка и отношений основаны на методе 11- 7248 последовательных сравнений, при этом проводится два тура опросов Экспериментальными исследованиями установлено отсутствие значительных различий результатов определения коэффициентов весомости по обеим шкалам. Практический опыт показывает, что при экспертной оценке качества товаров наиболее целесообразно применять следующую процедуру определения коэффициентов весомости [30].
Ознакомление экспертов со значениями коэффициентов весомости (и их обоснованиями), назначенными другими экспертами. Обоснование коэффициентов весомости — очень трудоемкая операция, поэтому применяется при ограниченном числе показателей (порядка 10—15). В противном случае экспертам предлагается дать обоснования только по некоторым показателям по их усмотрению или такие обоснования приводятся лишь в случае необходимости. После ознакомления с мнениями других экспертов во втором туре эксперт может ввести корректирование своих оценок, проставляя значения показателей весомости.
Конечным результатом применения методов опроса экспертов является получение групповых оценок, на основании которых составляется обобщающее заключение экспертной группы. Основные преимущества групповой экспертной оценки заключаются в возможности разностороннего анализа количественных и качественных аспектов проблем определения и/или прогнозирования отдельных характеристик товаров или их совокупности. Взаимодействие между экспертами позволяет значительно увеличить объем суммарной информации, которой владеет группа экспертов, по сравнению с информацией любого члена группы. К тому же количество факторов, учтенных при групповой оценке и влияющих на результативность принимаемого решения, больше, чем сумма факторов, учтенных одним экспертом. При групповой оценке меньше вероятность ошибки принятия в качестве основных факторов и показателей, не имеющих существенного значения для решения проблемы. Поэтому важным преимуществом групповой оценки является возможность получения обобщенного и более представительного результата. В большинстве случаев групповая оценка более надежна, чем оценка отдельного эксперта. Кроме того, коллективная ответственность позволяет специалистам принимать более рискованные решения. К недостаткам групповых оценок относятся:
при обсуждении оценок или наличии информации об оценках Других экспертов велика возможность конформизма, когда отдельные эксперты в силу неуверенности или иных причин могут соглашаться с мнением большинства. Несмотря на указанные недостатки, экспериментально установлено, что при соблюдении определенных требований групповая и* оценка более надежна, чем индивидуальная. К таким требованиям относятся:
Приемлемое распределение оценок может быть рассчитано математико-статистическим методом для выявления грубых погрешностей (ошибок) и их устранения. При этом могут быть использованы «правило трех сигм» или статистические приемы оценки вариации в рядах распределения. Более подробно вопросы проверки согласованности и достоверности экспертных оценок рассмотрены в специальной литературе. Групповая надежность оценок во многом определяется индивидуальной степенью надежности экспертов как одного из важнейших критериев их оценки. На заключительном этапе проведения товарной экспертизы применяются три группы методов: математико-статистические, аналитические и методы документального оформления результатов экспертизы. В этой главе подробно будет рассмотрена только первая из указанных групп. Аналитические методы как общенаучные методы подробно разбираются в дисциплине «Теоретические основы товароведения», а методы-операции документального оформления результатов экспертизы в главе «Организация проведения товарной экспертизы». Математико-статистические методы обработки экспертных оценок Математико-статистические методы обработки экспертный оценок — методы, предназначенные для повышения достоверности результатов оценки качества товаров экспертами. Подразделяются на четыре подгруппы методов: ранжирования, непосредственной оценки, последовательных предпочтений и парных сравнений. ранжирование — метод, основанный на расположении объектов экспертизы в возрастающем или убывающем порядке. Предназначен для решения многих практических задач, когда объекты, определяющие конечные результаты, не поддаются непосредственному измерению. Кроме того, отдельные объекты, характеризующиеся различной природой, оказываются несоизмеримыми, поскольку у них нет общей меры сравнения. Основанием для применения ранжирования служит необходимость упорядочения какого-либо объекта во времени и пространстве, а также в соответствии с измеряемым качеством без проведения точных измерений. И наконец, в ситуации, когда измеряемое качество в принципе не может быть измерено по причинам практического и теоретического характера. Процедура ранжирования состоит в расположении экспертом объектов в наиболее рациональном порядке и присвоении им определенного ранга в виде чисел натурального ряда. При этом ранг 1 получает наиболее предпочтительный объект, а ранг п — наименее предпочтительный. В результате получается шкала порядка, в которой число рангов равно числу объектов. Если два объекта имеют одинаковые ранги, им приписывают так называемые стандартизированные ранги, которые рассчитываются как среднее суммы мест объектов с одинаковыми рангами. Например, шести объектам присвоены следующие ранги:  Объекты 2 и 5 поделили 2-е и 3-е места. Их стандартизированный Ранг будет равен (2 + 3)/2 = 2,5. Объекты 3, 4 и 6 поделили 4-е, 5-е и 6-е места, а их стандартизироваанный ранг равен 5: (4 + 5 + 6)/3 = 5. В результате получается следующая ранжировка: 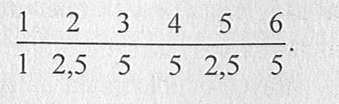 Таким образом, сумма рангов S„, полученная в результате ранжирования п объектов, будет равна сумме чисел натурального ряда: 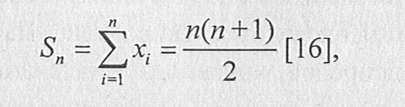 где х,- — ранг /-го объекта. Метод ранжирования редко применяется в чистом виде. Чаще всего он сочетается с методом непосредственной оценки или его модификациями (ранжированием по сумме оценок, комбинированным способом и др.). Метод непосредственной оценки состоит в том, что диапазон изменения какой-либо количественной переменной разбивается на несколько интервалов, каждому из которых присваивается определенная оценка в баллах, например от 0 до 10. Эксперт должен включить каждый объект в определенный интервал в зависимости от его значимости. В некоторых случаях для выбора наиболее предпочтительного фактора оказывается удобнее сначала провести оценку, а затем — ранжирование. Метод последовательных предпочтений — метод, основанный на сравнении отдельного объекта с суммой последующих объектов для установления его важности. Данный метод разработан У. Черчменом и Р. Акофом и предназначен для проведения сравнений с учетом определенных допусков. Основные из этих допусков заключаются в следующем:
9 если результат Qt предпочтительнее Qk или Qk предпочтительнее Qh то совместный результат Qi и Qk предпочтительнее Qt. Порядок представления результатов или их группировка не влияют на предпочтения. Процедура последовательных сравнений состоит в следующем. Эксперту представляется ряд объектов (показателей, факторов, результатов), которые необходимо оценить по их относительной важности (значимости), и он производит ранжирование. Наиболее важному объекту присваивается оценка, равная 1, а остальным объектам — оценки ниже 1 до 0 в порядке их относительной важности. Затем эксперт устанавливает, является ли объект с оценкой 1 более важным, чем сумма остальных факторов. Если важность объекта велика, то он увеличивает оценку Vi, чтобы она была больше, чем сумма всех остальных: 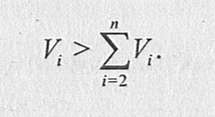 Если значимость объекта ниже, чем сумма всех остальных, то он корректирует оценки: 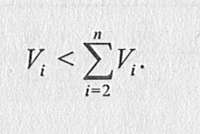 Далее аналогичной процедуре подвергаются все остальные объекты, значимость которых проверяется в сравнении с суммой всех оставшихся. Таким образом, используемая процедура состоит в систематической проверке оценок путем их последовательного сравнения. Метод последовательных предпочтений целесообразно примешь, если число сравниваемых объектов не превышает 7. При большем количестве объектов их необходимо разбивать на подмножества, включающие 6 объектов. В тех случаях, когда это невозможно, следует использовать метод парных сравнений. Метод парных сравнений — метод, основанный на сравнении объектов экспертизы попарно для установления наиболее важного в каждой паре. Для облегчения процедуры составляют матрицы парных сравнений, в которых все объекты (факторы) записывают в одном и том же порядке дважды: в верхней строке и крайнем левом столбце. Каждый эксперт должен проставить на пересечении строки и столбца оценку для двух сравниваемых факторов. В зависимости от того, какой фактор является наиболее предпочтительным, эта оценка будет равна соответственно 1 или 0. В главной диагонали такой матрицы проставляются прочерки или нули (табл. 6). Каждая пара факторов может сравниваться единожды или дважды. Существуют различные варианты частичного парного сравнения:
Таблица 6 Матрица предпочтений для ранжирования с помощью парного сравнения
Метод парных сравнений иногда сочетают с предварительным ранжированием объектов. При этом парное сравнение используется для уточнения предпочтительности отдельных объектов. В данном случае строится дополнительная матрица, в которой указывается доля с1учаев, когда один фактор оказывается более значимым, чем другой, общем числе полученных оценок. Вопросы для самопроверки
Каково назначение метода движения по уровням, и при каком Методе экспертной оценки он применяется. |
